QAD：マクローリン展開をマクロでやってみない試み～パート4～

マクロでやらないマクローリン展開シリーズもこれで最終回･･･！_{にするつもりですいちおう。}


マクローリン展開で出せるのは三角関数だけではありません。
ルートなどの無理数も、マクローリン展開で計算されています。


前回まで何度か出てきた円周率πも、マクローリン展開(より一般的にはテイラー展開)で算出されています。


この円周率の計算方法で「マクロでやらないマクローリン展開シリーズ」を締めたいと思います。


sinやcos関数の中身の角度は、1周を360度とする定義よりも、1周を2πラジアンと定義したほうがより根拠があると以前書きました。


では、sinxが1になる、あるいはcosxがゼロになるxは何度でしょうか？
90度ですよね。
ラジアンの尺度を使うとπ/2です。


三角関数を習うときにたいてい出てくる角度は0、30、45、60、90度のどれかでした。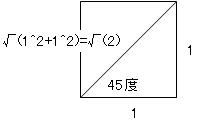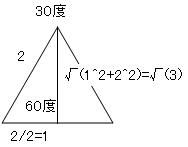
つまり2種類の三角定規の角どれかなわけです。
2種類の三角定規はそれぞれ、正方形と正三角形を半分にしたものでした。


だからこそ、無理数は√(3)や√(2)しか出てこなかったのです。


しかし、どこかテキトーに、sinx=0.642788になるxを答えよ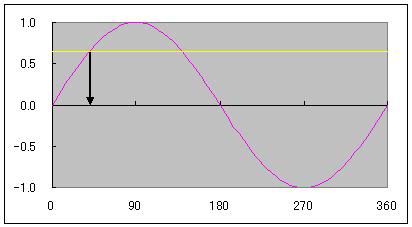

といわれるとどのように方程式を解いたらいいかわからなくなってしまいますよね。


そこで出てくるのが「逆関数」という概念です。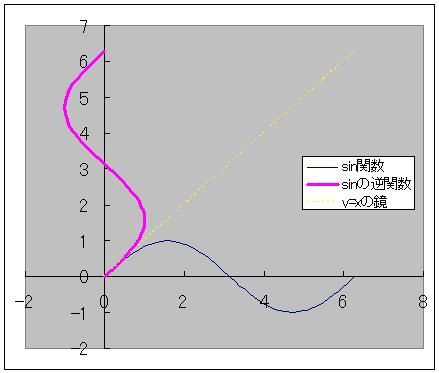

逆関数というのは、図のようにy=f(x)という関数をグラフにイメージしたとき
y軸とx軸、縦と横をひっくり返したような関数のことを言います。
ということは、y=xの直線に対して線対称なわけです。

sin関数の逆関数はAsinと書いて、アークサインと呼びます。
cosやtanもAcosやAtanと書いて、アークコサイン、アークタンジェントと呼びます。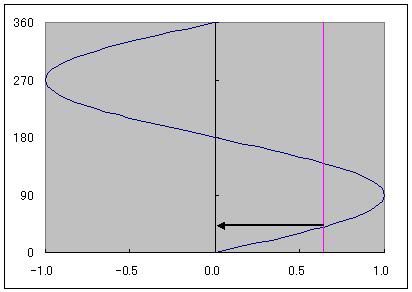

さきほどのsinx=0.642788は、x=Asin0.642788として答えればいいわけです。


このうち、アークタンジェントAtanを使って、円周率πを計算してやるのが今回の目的です。



tan45°は高さ1/底辺1で1ですよね。
ということは逆関数で考えると
Atan1=45度となります。

しかし、Atanの値は45度ではなくラジアンでπ/4となります。
このことを利用して、Atan(1)からπ/4を算出してそれをさらに4倍すると、円周率πが計算できるのです。

アークタンジェントのマクローリン展開は意外にも、タンジェント自身のマクローリン展開よりも簡単で
ベルヌーイ数なんてものも出てきません。

Atanx=∑(-1)^n・x^(2n+1)/(2n+1)

これだけです。階乗すら出てきません。なんだか拍子抜けしますね。
こんなんでどれだけの関数を再現できるのかと不安になるかもしれませんが大丈夫です。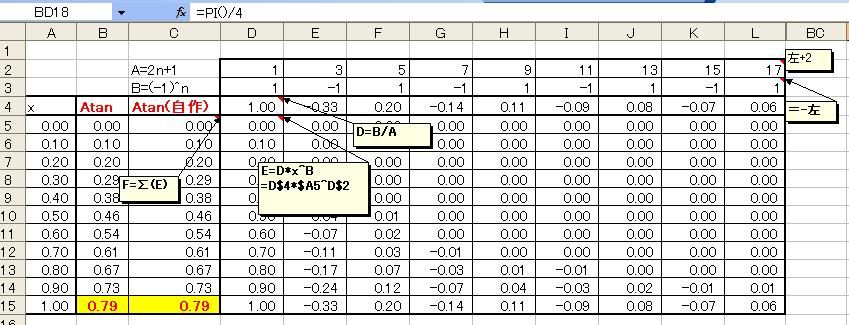

この表のx=1のところを見てください。
atanの値が0.79･･･(0.7854･･･)となっています。
これを4倍すると円周率3.14･･･が出せるのです。



トライアングラー

にほんブログ村

PAD：マクローリン展開をマクロでやってみない試み～パート3～

ずーっと前のこと、具体的には2011年の11月20日のことになりますが、
マクローリン展開をエクセル(マクロなし)で説明するっていうのをここの日記でやっていまして
ちょっと中途半端な状態で途切れていたのです。



不調が直ってきたので続きを再開しようかなと。

以前は、サイン・コサインなどの三角関数をマクローリン展開でいちから組み立てる話をしました。
パソコンは基本的に足し算(四則演算)しかできないので、
関数を足し算に還元する仕組みを紹介していたのです。

どこまでも続く数列の足し算、無限級数というのですが
基本的にこれを使えば関数を再現することが可能、という話でした。


しかしながら、パソコンのメモリや速さなどは有限なので
どこまでも足し算していっていたら巨大なパソコンになってしまいますし、いつまで経っても計算が終わりません。
そこで、ある桁数だけ合えばOKって割り切って、それに見合う数だけ数列を足しているのです。


しかし困ったことに、三角関数は関数の上限はあるのに、変数に上限がありません。
sinやcosはマイナス1からプラス1の範囲に収まりますが
関数の中に入る角度の数値は何回転でもできてしまうのです。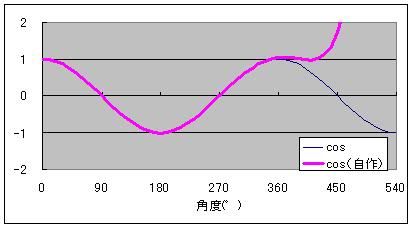


対策を取らずにコサイン720度とかを計算しようとするとおかしな数値が出ます。
なので、せめて360度の周期内に変数を抑える調整が必要なのです。


このとき、変数を周期的にする関数が使われます。
その関数とは、あまり演算です。

分数や小数を習い始めると、「あまり」の存在を意識しなくなりがちだと思います。
16を9で割ったら9分の16とか、1.77777･･･と考えて
1あまり7とかいう発想をしなくなる人がほとんどだと思います。



が、このあまりが大事になってくるのです。


三角関数の場合は、360度周期なので360で割ったあまりです。
たとえば361度は360度で割ったあまりである1度を、改めて変数に置き換えて
sinやcosを出すわけです。


ところが、三角関数の中の変数には1周が360の「度」という単位よりも
1周2πというラジアンを使ったほうがより適切であることから
周期を360度ではなく2πにしなくてはなりません。
つまり2π、無理数で割ったあまりを計算しなければならないわけです。



あまりを計算する関数というのもエクセルには組み込まれています。
mod関数というものなのですが

さきほどの16を9で割ったあまりを出したいときは
mod(16,9)と入力します。

この関数は何をやっているのでしょうか

たとえば、721度を360度で割ったあまりは1度ですよね。
これは、721から、360度を2回かけた720を引いていますね。
つまり、720/360=2という割り算を一旦計算しつつ、頭の片隅によけてあるのです。

721の場合は、721/360=2.0027777･･･の、整数部分だけを切り取って、小数点以下を切り捨てているとも言えます。
切捨てのための関数も用意されていまして、round関数と呼ばれています。


したがって
721/360の整数部分2を取り置きしておいて、
360に2をかけて、721から引くと、mod関数、「721を360で割ったあまり」=1が算出できるのです。


では逆に、マイナス10度はどうなるでしょうか？
-10を360で割ると、-0.027777･･･となります。
この整数部分は、実は0ではなくマイナス1です。
どういうことかというと、あまりは常にゼロ以上でなければならないのです。
といいますか、マイナスのあまりというのを「足りない」と定めて、「足りない」を「あまる」に置き換えると
あまりが必ずプラスになる。
といった感じでしょうか。


マイナス10度→-10あまる→10足りない＝350余る→350度

こういうわけです。

こう考えると、機械でも一律にあまりや周期が計算できるようになるのです。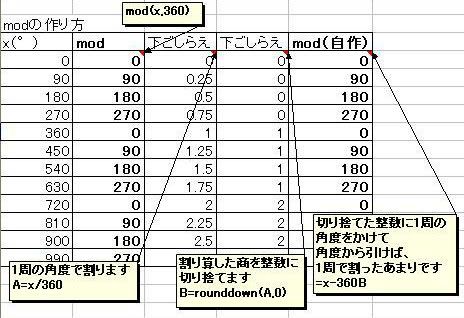


手順としては
関数の中身xを360度周期に抑えるためには
・下ごしらえとしてまずxを360で割り
↓
・割った結果の整数部分nを取り出し
↓
・x-360nを計算する。

これで、すべての角度が0度以上360度未満に収めることができます。



実は、この作業は無理数でも同じことが可能です。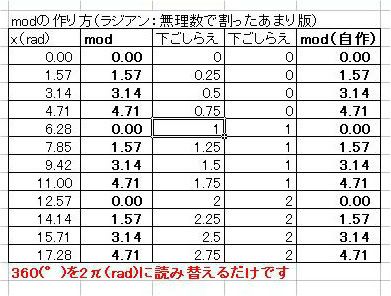



6.29radを2πラジアン周期に収めるためには
6.29を2π≒6.28で割ってその整数部分n=1を取っておき
6.29-2πn=6.29-2π・1≒0.1を変数に当てなおす。
これで無理数の周期化も完了です。
この変数を使って、改めてsinやcos、tanを求めれば、ちゃんとした値が出せるのです。


ぐるぐるモワレぐーるぐるモアレ　次回、最終回

にほんブログ村

GTC：マクローリン展開をExcelのマクロでやってみない試み～パート2～

前回の「展開せんかいマクローリン」は！
コサインのマクローリン展開に成功した管理人であった！

あらすじおわり
＝＝＝＝＝
さて、今度はサイン関数のマクローリンもやってみることにしましょう。

sin関数は

sin(x)=∑(-1)^n・x^(2n+1)/(2n+1)!

なのですが、ここはひとつ邪道に行ってみることにして、
cos(x)=sin(x+π/2)

であることを使ってみようと思います。
つまり、x'=x-90°として、cos(x')をsin(x)としてみるのです。

そうすると、マクローリン係数はコサインのときそのままに、サインのマクローリン展開ができてしまうではありませんか。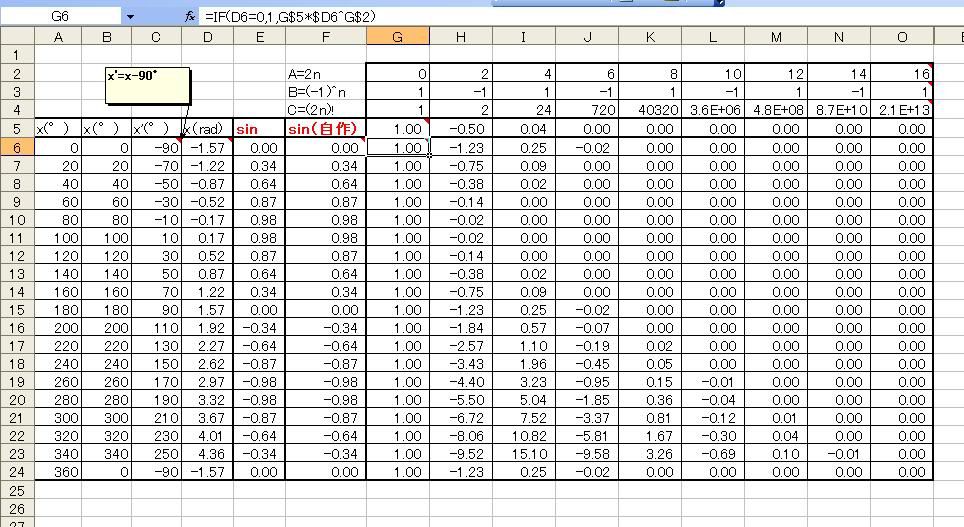





ついでにタンジェントのマクローリン展開もやってしまいましょう。
wikiにはB(ベルヌーイ数)とかいうよくわからない数を使うとかいてありますが心配要りません。
タンジェントはコサイン分のサインじゃないですか。

つまり、cosもsinも作ってしまったわけですから、
tan(x)=sin(x)/cos(x)
で計算してしまえばいいのです。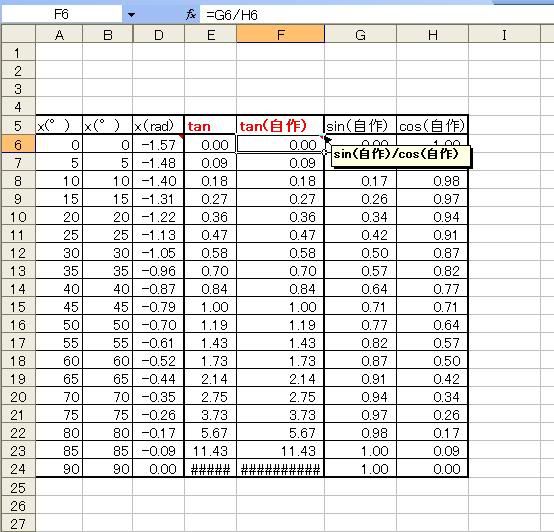

_{本当はsinもtanも素直に展開するべきなんです。
PCさんはsinとcosを作ってからtanを計算するなんて回りくどいことしたくないでしょうからね。
でもベルヌーイ数とか出てきたら萎えるじゃないですか。
ただ、sinの展開の仕方、これは僕のシュミ一筋です。}


つづく？→続いた！



にほんブログ村

FTC：マクローリン展開をExcelマクロでやってみない試み

高校の数学でマクローリン展開ってのを習ったじゃないですか
そんなん習ってない人のことなんて僕は習ってないんでお構いなしで話しちゃうじゃないですか


あれです、たとえば
100万円に月0.01%の利子がつくとしたら3ヶ月後にはどうなる？っていうのを計算するとしますよね

100万×1.0001^3が3ヶ月後の金額じゃないですか
1.0003を3回かけるわけです。
でも0.01%=0.0001が1に比べてはるかに小さいとき
(1+0.001)^3≒1+3・0.0001に近似できるよーって話


マクローリン展開はそんな感じの話です。
もう少し広い意味ではテイラー展開なんですけどね。


コイツがどんなところで使われているかっていうとPCの中はコレだらけです。
デジタルコンピュータのPCさんは基本的に足し算しかできないので。
四則演算だってPCさんは足し算にしてやってるんですよ。

まず引き算は「マイナスの数を足す」と解釈します。マイナスの数はプラスの数の補数で表現可能です。

次に掛け算は「足し算の集まり」と解釈してもいいですし、「桁をシフトさせる」と解釈してもいいです。
12を10倍した120は12を左にシフトさせたと考えることができます
これを10進数ではなく2進数で考えると、12→1100を2倍するには左にシフトさせて11000にしてしまえば24の完成です。

逆に24→11000を半分にしたければ右にシフトさせて、1100にすれば12に戻るので、割り算もこうすればできることになりますよね。



じゃあエクセルのサインとかコサインとかはどうやってんの？といいますと
別に全部暗記してるわけじゃないんですよ。
かといってcos15°を30度の半分なので半角の公式を使っている、というわけでもないです。

じゃあどうやっているのかといいますと、これも全部足し算に戻して計算しているわけです。
そこでマクローリン展開が必要になってくるわけです。

コサイン関数をマクローリン展開すると、ある数列が顔を出します。
これをマクローリン係数と呼ぶことにしましょう。
マクローリン係数にcos(x)の中身のx、xの何乗かをかけたものをマクローリン数列と名づけるとして
これらを全部足したものはマクローリン級数と呼ばれています。

「級数」というのは数列を足したものを言います。
たとえば1+2+3･･･+7+8+9+10=55
これも級数です。
ただし、1から10までの足し算です。

どこまでも果てしなく足したものを「無限」級数と呼びます。


マクローリン展開というのは、マクローリン係数にxの何乗をかけてマクローリン数列にし、
それらを全部足して無限級数にすることでどんな関数でも表現できるよ

というものなのです。つまり、どんな関数も足し算だけで表現可能なのです。
ただし、どこまでも足した場合です。

限られたごく一部の関数たちは3回足しただけで出来上がるのもいますが
たいていの関数は基本的にどこまでも足します。
しかしPCさんはそんな無限に立ち向かえるようなスペックを持っていないので
「途中」で足し算をやめます。
その途中までの係数を、PCさんは暗記しているわけです。

暗記といっても理解に近いかもしれません。
マクローリン係数は整数ではないものの数列なので、ある規則にのっとって変化します。
PCはその規則を覚えているといったほうがいいかもしれません。



では実際に、コサインのマクローリン展開をやってみて、エクセルのコサインと合うかどうかやってみましょう。

こういうとき、普通はプログラミングをしてマクロを組んでユーザーの定義した関数を作るのですが
僕はプログラミングが苦手なので、マクロは今回一切作りません。
どうしてプログラミングが苦手なのかというと、バグがよく見えないのです。
だから、いちいちセルに表示して確認しないと嫌なのです。

この図を見てください。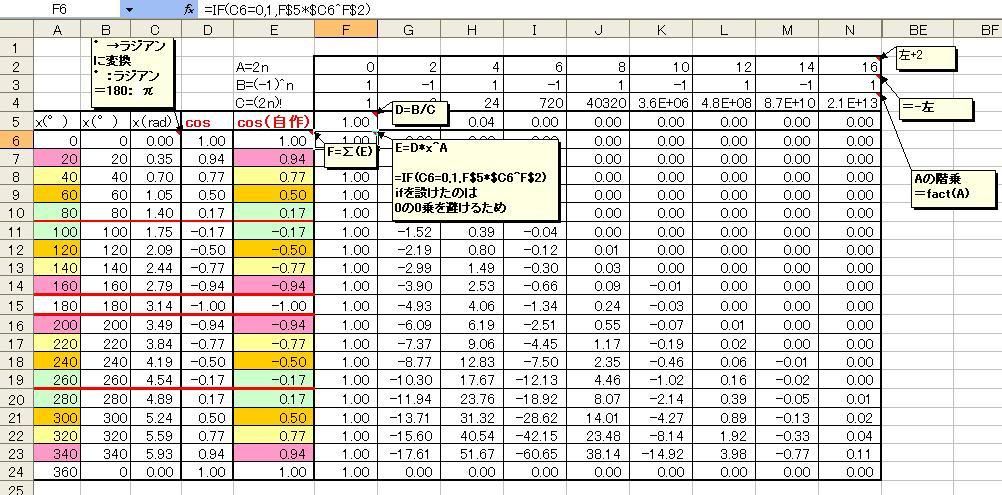

cos(x)はマクローリン展開すると

cos(x)=∑((-1)^n・x^(2n)/(2n)!)

で再現できるのですが

nを整数として
A=2n←0、2、4、6、8、10･･･などといった偶数の数列という意味です
B=(-1)^n←マイナス1のn乗、つまりプラス1とマイナス1を交互に繰り返す数列という意味です
C=A!←（「faxt(A)」や「A！」はAの階乗数列、たとえばfact(5)や5!は1・2・3・4・5を意味します）
D=B/C←マクローリン係数
E=D・x^A←マクローリン数列、そして
最終的に表現したい関数をF=∑(E)←マクローリン級数　∑(しぐま)はです。

と、順を追って表現しています。

エクセルに元々入っているコサインと自作のコサインを比較してみると、一致しているのがわかると思います。


ただ、注意事項として、cosの中身のxは°ではなくラジアンという単位を使わないと数値が合わないです。
°というのは一周が360°という単位ですが、どうして1周360°なのかという根拠は曖昧で
約数を多く持つからという意味合いしかありません。
きっと6人とか9人とかでケーキを分けたかったとかそういう理由だと思います。いやまじで。


それに対してrad(ラジアン)は1周を2π(円周率の2倍≒6.28)とします。
これは半径1の円周という立派な根拠があります。




次回の「展開せんかいマクローリン」は！
新キャラ登場！sinとtan。でもなぜにこのブログではcosから始まった！？
次回、「マクローリン展開をExcelのマクロでやってみない試み～パート2～」
おたのしみに


maccrosof介

にほんブログ村

VGC：マクローリン展開をマクロでやってみない試み

ゆかり先生「マクロなしでもなんとか生きていけるものよー」



にほんブログ村