ずっと探してたアレの答えがこんなところで何年も待ってた！雑記

ユークリッドの互除法

以前説明を見たときは何言ってるかわかんなくて挫折したんだ。

アドイン追加で最大公約数GCD関数が使えるようになってから1年以上たつかな

そういえばGCDってどうやって出来てるんだろう？

って疑問に思って

アドインなかったら使えないっていうのはどういう意味合いに取れるのか考えてみた。
・ユーザーの問題
と
・スペックの問題

が思い浮かんだ。

もしスペックの問題だったら
たくさん配置したら動作がより重くなるような関数なのかもしれない

2重以上のループしてたりして


と思ってちょっとぐぐってみたらまず当たったのが素因数分解で
いやでも素因数分解だとちょっと効率悪すぎないか？って根拠なしに疑問に思って
根拠なしにユークリッドの互除法あたりかな？って思ったらドンピシャ。

素因数分解よりもはるかに効率的に最大公約数を見つけ出すことが出来る。
こんなすげー武器が紀元前にすでに発見されてたなんてなー


最近はwikiの洗練もそうだけど、動画で解説してくれる人もいるから(僕の)理解が早くて助かる。


で、そのwikiなんだけど
よく見たら右のgifアニメが秀逸だった。

と思ったら思い出した！
これアレだー！
計算盤尺だーー！！








ところで、3Dプリンタで声帯模写して中に誰もいませんよボカロとかやっちゃう人そろそろ出てこないですかね

にほんブログ村

数学ガール～フェルマーの最終定理～クライマックスへジャンプ

1つしかなく無数の元を持つ有理数体Qの代わりに、無数にありながら有限個の元を持つ有限体Fp(pを法としたあまり：モジュロ演算)で楕円曲線をしらみつぶし的に考えることができるらしい。


たとえば5で割ったあまりで楕円曲線y^2=x^3+xが成立するかどうかを調べるとこうなる。

5×5=25個の組み合わせの中で成立するのは7つだけ。
これは、楕円曲線の「重解を除く」という条件があるためらしい。


以下に素数p：2～29を法とした楕円曲線の表(表はimageです)へのリンクを貼る。

2,3,5,7,
11,13,17,19,23,29

pに対する成立個数s(p)を改めて表にまとめるとこうなる




ところで
実に数学らしい薮蛇現象があって
保型形式
たとえばこんなん

の無限積をqの30次まで展開すると
qの次数について次のような級数となる。

k次の数列をa(k)とすると、以下のような表(表は図です)になる。


展開の方法としては、30次以上になるものを大文字のQでまとめて無視してしまい
kを徐々に増やしていき、30次未満が出なくなるkまで進んだらストップ
ということをやればいいそうだ。










PCは解析的計算においても便利だな。コピカペはできるし字がきれいだ。


qの次数を素数pに限りa(p)としてから、楕円曲線の法(素数p)ごとに成立する数s(p)と比べると
(aには4の倍数次のときの係数しかないので)

a+s=pが成立している。


なにやらこのような手続きを経て、フェルマーの最終定理は晴れて予想から定理になれたらしい･･･
なんだかよくわからないが、雰囲気だけは醸し出されたようだ
と、僕の主観ではそう思った。
俗に言うブルーバックス現象とか、きつねにつままれたような入門書現象とかそういうやつである。

まあ、入門書ですべて理解できたら専門書なんていらないんだ。
全人類が研究者になってしまうますしおすし。


Fermata　Last　Teiri４

にほんブログ村

ピタゴラ・ジュース・メーカーのつづき(数学ガール)

ピタゴラジュースメーカーの真の実力を発揮するときが･･･ｷﾏｼﾀﾜｰｰｰｰ！！ｽﾞｺﾞｺﾞｺﾞｺﾞｺﾞ･･･

ピタゴラジュースメーカー～前回までは～

直角三角形の三辺の長さは三平方の定理で決まる。
この3辺が整数になるときの3辺をピタゴラス数という。
ピタゴラス数を自動で生み出すには、mとnという整数を用いて

底辺=m^2-n^2
高さ=2mn
斜辺=m^2+n^2

という条件で無数に生み出せることがわかった。

ただし、mとnには制約があり
・m>n
・mとnの最大公約数は1(カブらないように→原始ピタゴラス数)
・mとnのどちらかが偶数でどちらかが奇数

というものだった。

前回は手作業でmとnを出していたが、
mもnも大きな数になると手間がかかるため自動化したくなる。


●●までのmとnを求めたいとしたとき(今回は30まで)
初期のnはまず1
初期のmは初期のn+1

次以降のnは、「前のm+2≦上限●●(今回は30)なら前回と同じnを、>上限なら前回のnに1追加」
また、2番目以降のmも「1つ前のm+2≦上限なら前回のm+2を、上限を超えたら同じ回のmに1追加」

とした。

式にするとこうなる
n(1)=1
m(1)=n(1)+1


n(k)=if(m(k-1)+2<=上限,
　　n(k-1),
　　n(k-1)+1)

m(k)=if(m(k-1)+2<=上限,
　　m(k-1)+2,
　　n(k)+1)

で、互いに素のカブったやつを消すために判定項目でmとnのGCD(最大公約数)を求め
1になったやつらだけをフィルタリングで抽出。


というわけで･･･



186個を三角比の形にしてグラフにまとめてみましたー！




にほんブログ村
スイカ三角面

ピタゴラ・ジュース・メーカーの作り方(ついでにエクセル講座)

テレビのアス比は３：４でした。
じゃあ20インチのテレビの横幅はいくつかといいますと16インチちょっきりでした。
これは、20インチが対角線の長さで、縦：横：高さの比が３：４：５という整数比になっているからです。

長方形を対角線でぶった切ると直角三角形が2つ出来ます。
この直角三角形の3辺の比は、一般には無理数です。
ピタゴラスの定理に2乗が含まれているからです。
底辺^2+高さ^2=斜辺^2でしたね。

ですが、時々整数の比、つまり有理数(分数)になります。

これがピタゴラス数です。


また、アス比３：４のテレビは20インチだったり16インチだったり22インチだったりいくらでも選べます。
アス比３：４のテレビを唯1つ無2の規格にしたい！
という願望があったとして、3インチ：4インチ：5インチなどという、最大公約数が1の整数にしたものを原始ピタゴラス数といいます。
また、「最大公約数が1」というのを「互いに素である」といいます。



原始ピタゴラス数はそう簡単に姿を現してはくれません。
たとえば底辺と高さに100までの整数をランダムにぶち込んだとして(round(100*rand(),0))
1000回試したところで整数比になれるのがせいぜい30個程度ですし(ピタゴラス数：mod(斜辺,1)=0になる条件)
ほとんどは相似な四角形なので除外され(原始ではないわけです)
今回はカブりませんでしたが合同な四角形(というか直角三角形)を除外するとたった2つ程度しか残りません。

今回の試行では
5:12:13
45:28:53
の2つでした。



実は、原始ピタゴラス数の斜辺と高さの間には
どちらかが奇数だともう片方は必ず偶数
という性質があるのですが、それを見つけるまでの準備が手間になってしまっては仕方がありません。


そこで登場するのがピタゴラジュースメーカーという原始ピタゴラス数を効率的に搾り取る装置です。
と、「数学ガール」に描かれていました。

＝＝＝＝＝＝＝
底辺・高さ・斜辺の種になるmとnという自然数を考えると

底辺=m^2-n^2
高さ=2mn
斜辺=m^2+n^2

で、原始ピタゴラス数が求まってしまうのです。
＝＝＝＝＝＝＝


ただし、
mとnはなんでもいいわけではなく
・m>n
・m⊥n（mとnは互いに素、最大公約数GCD(m,n)=1)
・mとnどちらかが偶数でもう片方は奇数(XOR(ぐうm、ぐうn)=false)
※ちなみに偶数かどうか「ぐうm=mod(m,2)」で定義します


では実際に、エクセルでピタゴラ・ジュース・メーカーを作ってみましょう。

まず、mとnを格納する2列を用意します。
小さいnのほうを左側にしておきます。


次に、nに値を入れてみましょう。


ここで、あまり多すぎても切りがないのでmとnを10までに絞ることにしますと
n=1なら、mは2～10までの偶数になります。

ではn=2にしてみましょう。
mはnより大きい奇数なので、3～10の奇数になります。

そしたらn=3にしてみます。
mは4～10の偶数になります。
m=6は最大公約数が1ではないので除外するのですが、この除外処理はあとでフィルタで行うことにします。


このように作業を続けていくと、1つのnにつきmは基本的に1つ飛びで数えていけばいいことがわかります。
1つ上+2です。
また、1つのnにつき最初のmはn+1であることもわかります。


それでは、互いに素でないmとnの組み合わせを除外しましょう。
最大公約数を求める「GCD関数」が、数学・三角のジャンルに入っていなければ、「分析ツール」のアドインを登録する必要があります。

mの右側に「互いに素」判定の列を設けて、gcd(m,n)を取りましょう。
あとでフィルタリングで除外します。



ここまでくれば、あとは
・底辺=m^2-n^2
・高さ=2mn
・斜辺=m^2+n^2
を計算すれば、ピタゴラス数の出来上がりです。


いちおう、ピタゴラスの定理どおりになっているかどうか判定しましょうか

斜辺^2-底辺^2-高さ^2の列を設定すればいいので

このように全部ゼロになることがわかると思います。


3辺全部整数なのはおｋですよね？
整数判定は、1で割ったあまりが0になればいいので、条件はmod(●,1)=0です。

3辺が互いに素かどうかの判定もしておきましょう。
GCD(底辺、高さ、斜辺)を計算すればいいのですが
ちょうどmとnの「互いに素判定」で2以上の数が出たところだけが、3辺の「互いに素判定」でも2以上が出ていることがわかると思います。


ここまでが、ピタゴラス数の一覧です。
黄色い部分のうち
27:36:45と75:100:125は3:4:5
45:108:117は5:12:13と相似なので、原始ピタゴラス数ではないわけです。

原始ピタゴラス数は、GCD(m,n)でもGCD(底辺、高さ、斜辺)でもどちらでもいいのですが、
とにかく互いに素判定が1のものだけフィルタリングしてやればおｋです。

黄色の目印は手動でも構いませんが、条件付書式でつけると効率的です。
列選択をして、「書式」→「条件付書式」でダイアログを出します。
「セルの値が」「1に」「等しくなければ」「背景を黄色くする」とすれば、とりあえず印はつきます
(数値以外が黄色くなるのを防ぐには列参照ではなく複数セル参照のほうがいいですね＾＾；)




オートフィルタで構わないのですがフィルタリングしましょう。
一番上の項目行に最低2種類の書式設定をしてやれば、自動的に表だと認識してくれますので
あとは「データ」→「フィルタ」→「オートフィルタ」のチェックをオンでオートフィルタモードになります。
項目すべてが自由にフィルタできてしまいますが、今回は2つのうちどちらか1つの「互いに素」の▼ボタンを押して
「1」だけを選別すればおｋです。黄色くつけた目印が消えたかと思います。




定義や表を見てわかるとおり、この装置で搾り出したピタゴラス数は、底辺が奇数、高さが偶数に偏る性質がありますが、入れ替え可能なので問題ありません。

最初のほうで書いた、底辺と高さどちらか一方だけが偶数になるという性質をいちおう検算してみます。
底辺が偶数であるというフラグ「ぐう底辺」はmod(底辺,2)で計算できます。
2で割ったあまりなので0か1しか出てきませんから、そのままbooleanとして扱ってしまいましょう。
XORという関数がないのでa=ぐう底辺、b=ぐう高さとして
XOR(a,b)=OR(and(Not(a),b),and(Not(b),a))
で作ってやりますと
全部trueになることがわかるかと思います。




この性能を発揮させるために、50までの整数をランダムに、底辺と高さで2500ペア試して
よりすぐり5個の底辺・高さの偶奇判定

XOR(a,b)=OR(and(Not(a),b),and(Not(b),a))



を行ってみました。＾＾




ピタゴラ・ジュース・メーカーの定義を見ると、mもnもどこまでも大きくしていけるので
原始ピタゴラス数だけでも無限に作れることがわかると思いますが
これはあくまで整数比なので、この隙間を縫って実数のアスペクト比が存在することがわかります。
つまり実数の無限は整数の無限より濃度が濃いのです。(合ってるよね？)



つづく。

にほんブログ村

ピタゴラ・ジュース・メーカー備忘録

ピタゴラスの定理a^2+b^2=c^2のa、b、cが原始ピタゴラス数(既約な自然数)であった場合

aとbの間には


XOR(ぐうa、ぐうb)=1が成立するらしい。

つまり、aとbのどちらかが偶数で、どちらかが奇数。
両方偶数や両方奇数はあり得ない。

ただし、ぐうx：mod(x,2)
(偶数でフラグが立っても奇数でフラグが立っても、どうせXORにかけるので統一されていればどちらでもいい)



b^2=c^2-a^2にしたら
=(c+a)(c-a)になる。
その発想はなかった！なんでや！


数学ガール

にほんブログ村
間違えたXOR(ぐうa、ぐうb)=0だ＞＜

コンピュータ系燃費計

ビュンビュン系燃費計って面白いですねー。特に平均燃費計


簿記でいういわゆる総平均法みたいな？


ガソリン消費量Qと走行距離Xの瞬間ごとの値QiとXiが順番iごとにあって
瞬間ごとの燃費ηiがηi＝Xi/Qi
であらわされるとしますっしょ？

したらその平均が
平均燃費＝Average(ηi)＝∑(Xi/Qi)/∑(i)＝∑(Xi/Qi)/n

って単純に燃費を平均化するわけじゃないんすよ

燃費＝∑(Xi)/∑(Qi)　いわばAve(Xi)/Ave(Qi)
割ってから平均すんじゃなくて、平均してから割るような感じっすよ



それでこの燃費計、自動車についてるものはデジタルなので、給油ごとに問答無用にリセットされるなんて設計ではないべきで
好きなときにボタン長押しとかでリセットできちゃうんですね。

そしたらリセットしたての燃費ってじゃじゃ馬のようにあがったり下がったりで
そりゃぁ分母も分子も数えたてのゼロ付近から発散していきますからね
燃費はまだ収束しませんよねｗｗｗ

そこで思いついたんですが
「平均燃費計とリセットボタンがあったら瞬間燃費計いらなくね？」
って話っすよｗｗｗ

リセットしたての燃費が近似的に瞬間燃費にほどなく近いですからね
っていうか瞬間燃費の使い道とか考えたら余計な機能ｲﾗﾈって感じですよ＾＾



ところでコイツって計測器＜メータ＞であると同時に計算機＜コンピュータ＞なんすよ本質的に。


コンピュータとくれば、
アナログコンピュータで燃費計つくりてーってなるでしょｗｗｗ僕は機材がないけど


以前どこかで、円周率を出すためだけに電子工作でアナログコンピュータを作ったっていうサイトがありましてね
っていうかアナログコンピュータって目的のためだけに1つこしらえなきゃならないところが難点ですよね。

まあ、素人が回路図アップするくらいならアップスンナ、ｸﾞｸﾞﾙﾅｶｽって言いたい気持ちはわからないでもないです
いや全然わかんないです＾＾

それくらい図面作る側も実際に作る側もシビアな状況に加えて
目的のためなら手段を1つしか選べないっていうんでしたら
そんならもうアナコンやーめた！
ってもなりますよね＞＜


あ、そんな暗い話はさておき；
そのアナコンでπ算出したサイトに出向いたきっかけがですね

オペアンプって掛け算苦手なんすよ･･･

オペアンプの得意分野は加減微積っていいますし

だからどうにかして掛け算と割り算をできるように･･･
そう。苦手どころじゃなく出来ないんですよ彼は掛け算がっ！

なので見に行ったんです。そのサイト。

そしたら目から鱗のような羽毛恐竜が落ちてきましてね
電子計算尺！

NJM4200

こいつはすげーですぜ･･･！

計算尺って一度対数を取ってから加算して指数を取って元に戻すことで
掛け算を足し算のようにやっちゃう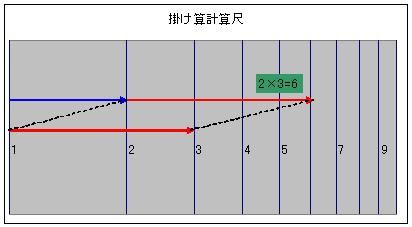



たとえばですね3×2=6を
log(3×2)=log(3)+log(2)≒0.48+0.30=0.78≒log(6)
といった風に掛け算を対数同士の足し算として演算してくれるわけです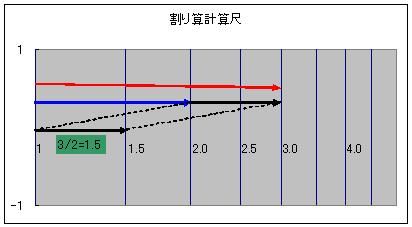




同様に割り算は対数同士の引き算になるので
log(3/2)=log(3)-log(2)≒0.48-0.30=0.18≒log(1.5)
となるわけです。



そうやって長さとか電圧とかの物理量そのもので計算しちゃうのをアナログコンピュータっていって
デジタルにしろアナログにしろ機械式と電子式があるんですけど
計算尺を電子でやると、半導体の対数的な特性が天然に使えちゃうという
もし半導体に対数特性なかったらどうしてたんだよ！そんなもしはない！
そんな危うさがたまらない！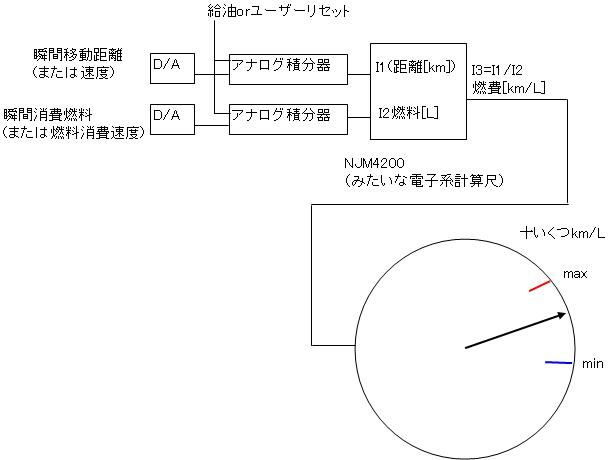









こんな感じで実装したら楽しいだろうなぁー(ウチは機材ないけど)
アナコンなんで上下限は必要なんで、給油時の問答無用リセットはつけさせていただきたいですどねｗｗｗ


でも表示がアナログだったらリッター十数キロまでは見えてもコンマいくつが見れないなどうしよう
ノギスのバーニアみたいなモアレ現象でも使ってやろうかふひひｗｗｗ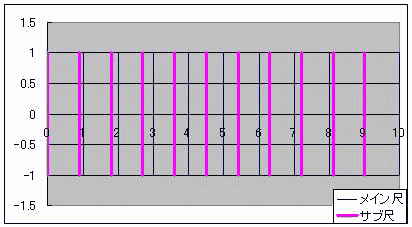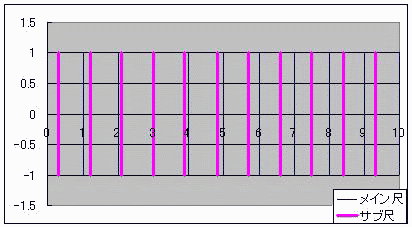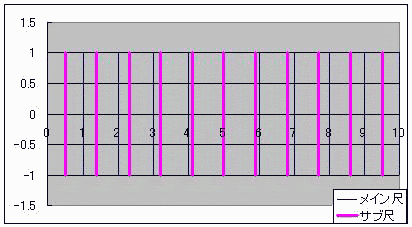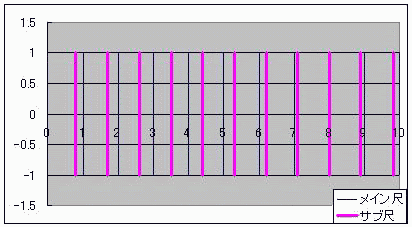



もしメカニカルな針表示とかにできれば摩擦の力でメモリスタもどきの記録素子をおおおおｗｗｗｗ

はぁーアナコンでデジコンだなぁー
実用性はともかく、楽しそうだなぁー

にほんブログ村

BVC：アナログでデジタルでハイブリッドなコンピュータ

以前、

算盤のようにデジタルでありながら、計算尺のようにアナログな計算器を「計算盤尺(けいそろばんしゃく)」と名付けよう

としたところで具体案が見つからずに困って放置していたテーマがあった。
ただ、当時からおおよその見当はついていた。


それは案外身近にあったのかもしれない。


ノギスっていう精密定規があってな

変わった方法で1mm以下の精度を出すんだ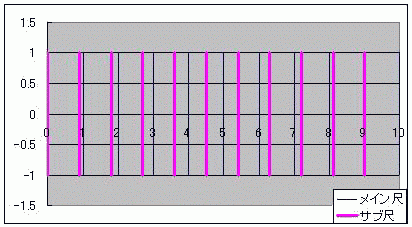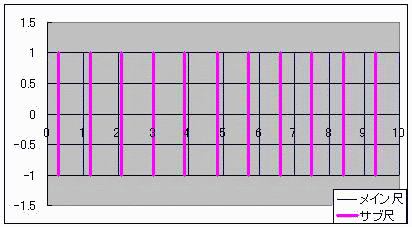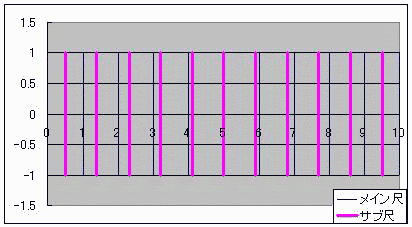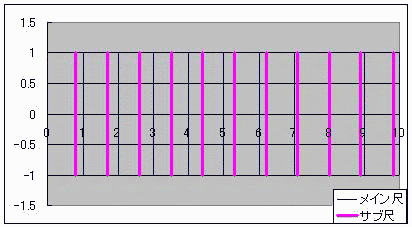


メインの定規の横にバーニヤっていう副定規が添えられててな
こいつ自体は0.9mmごとに目盛られていて
メインとサブの目盛がちょうど重なったらそこのサブの目盛の数字が100ミクロンの桁の数字なんだそうだ。
メインの目盛が1mmごとなのに、100マイクロメートルが測れるんだよ

この原理にはモアレの理屈が使われている。
モアレというのは、時間で言う「うなり」の空間版のようなものだ。
ストロボにも似ている。
これは周期構造によるもので、
周期構造をフーリエ変換すると離散、つまり不連続とかデジタルな量が現れる。


しかしながら、長さという物理量そのもので演算しているからアナログつまり連続的な演算でもある


ノギスは僕の追い求めていた計算盤尺(けいさんばんじゃく)そのものだったんやーー！！



お前、ただ計算盤尺が言いたかっただけだろ！とはドーラの言い分である

にほんブログ村

QJC：計算尺と算盤とハイブリッドコンピュータ

なんだろうなぁ･･･デジタルなそろばんとアナログな計算尺をモジュロ演算(あまりの演算)で組み合わせた

「モジュロ計算盤尺(ケイソロバンジャク≠ケイサンバンシャク)」

を思いつきかけた気がしたんだけど、疲れているせいなのか具体化までの思考が続かなかった。

計算尺に算盤の碁石みたいのをいくつも重ねて、
モジュロ演算を行うんだとしたら
アナログでもデジタルでもあるハイブリッドな計算機が作れないかなー？
って思ってね

具体的に対数方眼紙と線形(リニア)方眼紙を使って見える化しながらやってみたんだけど、
なんかイマイチ、ピンとこなかった。

まあいいや

あ、そういやノギスのバーニヤとの関連はないんだろうか


地デジ　地上波デジタル　アナログ　放送　終了
そういえば今日も忘れるところだった。
24日の11:59:59まであと1週間と3時間1分41秒くらい

にほんブログ村