|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
配信が増えている影響なのか、あずまんがコミックのコンパクトさをアニメ化したようなアニメが増殖してるな。うむ・・・これはこれで決して短すぎないような気もしてくる・・・!
そしていつの間にか進んでいた、作品の「メディアミックスtoソリュートミックス」!! な、なるほど・・・! フォトンの波としての媒質って結局なんなのよ?って問われたら決して納得する答えが出せない今の物理学・素粒子論を比喩しているのだな!? 自然は真空を嫌う  まさにそのとおりだ! 量子真空は俺たちの求める真空とは異なる・・・なんつうか・・・「コレジャナイ感」があるよな! 結局そこに無なんてねえだろ!みたいな 溶質(ソリュート)が増殖して溶媒(メディア)と区別がつかない感じになっているわけだ 水1:牛乳1、それ牛乳何割?みたいな  にほんブログ村 PR 「タイムトラベル11の理論」のニコニコ大百科に行き着いた。 まあ複数あることは知っていたし 2つの理論以外はどこかで聞いたことのある理論ばかりだったのだけど 1つ目の理論が「中性子星でのタイムトラベル」だったことが意外だった。 ただ単にウラシマ効果の「加速」を「重力」に置き換えただけじゃないか・・・ しかも未来への片道切符だし現実味を「加速」より薄くしてどーすんだ・・・ ただ、よく考えてみると 中性子星人というのはブラックホール星人とは違って、SFでわりと具体的に描写済みなわけだし 単に元々中性子星に住んでいただけでタイムトラベルできるかもしれないというのは結構お得な話なのではないか。 たとえば中性子星の大地は実は結構ドロドロの底なし沼で それに浮かんだり沈んだりして生活のエネルギーを得ている中性子星人たち 沈むと重力が軽減されて、「逆・ウラシマ効果」をもたらす つまり、「自分だけ周りより歳をとる。」 (※ただし、この方法では決して時間を逆行しない) いや待てよタマテバコ効果のほうがわかりやすいか そう考えると、我々地球人が中性子星に移住するようなことを考えずとも ネイティブな中性子星人とネットでやりとりするだけで 中性子星人の因果観というのがどれだけ地球のものと異質なのかがわかるかもしれない あるいは、我々地球人が考えてきた因果観のモロさを中性子星人とのネット会話で、露呈できるかもしれない もし中性子星人の私生活の中で同時性の相対性が身近なものだったら、それだけで地球人としてはお買い得だろう それにしても「0が過去で1が未来」 といいうフレーズの直後に 「今はどこにもない」というフレーズがなかったら そして、 スイヘーリーベ並みに明るい曲調だったらなんともお間抜けな感じに聞こえてきそうで困る ====== よく考えてみるとシゥタケ゛はSFの作りづらい現代においてかなりよくできたほうのSFだろう タイムトラベル作品を作るうえで、真面目にやろうとするとたいていはタイムパラドックスに悩む。 1.タイムパラドックスで悩むかどうか 2.タイムパラドックスを起こすか、起こさないか。 3.タイムパラドックスを起こすとしたらパラレルワールドの要素を取り入れるかどうか。 ところがここで、パラレルワールドの要素を取り込むと話がややこしくなり また同時に、過去を改変する前の世界線に戻ることが原則的にはできなくなるため、共感が得られにくい しかしながらシュタインズゲートという作品は タイムトラベルの方法がいくつもあって煩雑としていることを逆手に取り、主人公たちが利用するタイムトラベルの方法を1つに絞らないことで わかりやすくもかつ魅力的なストーリーを引き出している。 その上、一旦パラレルワールドを展開しておいて あえて唯一の世界線を選択するといった手法はかなり共感を得る展開方法だっただろう リーディングシュタイナーは実は誰もが持っていて、それでいて個人差がある能力である、というのはどのくらい活かされていたのだろうか、ゲームをやっていないのでその辺はよくわからないが、とても夢のある設定だと思う。夢だけに。 夢だけど夢じゃなかった!というのは具体的にすればするほど魅力が沸いてくるものなのではまいかろうか。 征服王さん実にホモホモしい。 俺だ・・・京都のマッドノヽウスに住んでいる鳳凰院平等堂だ。 いつも ハック・トゥ・ザ・メール♪トゥットゥルー! いや、まゆりはあくまで幼馴染であって決して嫁というわけでは・・・ うわ何をするルカ娘は男だ!あえてもう一度いうイカ娘は男だ!そんなもの毎日見てるから見せんでいい!  にほんブログ村
量子きのこ、前回までは!
ほうじ茶ラテのラテ部分をそのままに ほうじ茶→ウーロン茶(お茶だしな!) ガムシロップ→メイプルシロップ(葉っぱだしな!) に変えておいしく実験を楽しんでいた。 あらすじ終わり。 ====== 今日はいよいよフェイズ・シロップ→フェイズ・カルピスに移行する! しかし最近はカルピスからミルトンに、我が家のシェアが変わったのでミルトンに変更 だがちょっと待ってほしい! それだと牛乳と酸で「フルーチェ現象」がおきてしまうではないか!! フルーチェ現象とは、酸味の有る (カラーとフレーバーはそれぞれ、太陽の果汁サンレッド、水の果汁レインブルー、鳴神の果汁サンダーイエローの3種類の国家機密的資格が存在する) カルピスの悲劇をミルトンで繰り返してはならない! よって実験は中止だ! どうもこんにちは平等院法魔です。ヽ(*゚д゚)ノ ダンナがお騒がせいたしております。 33にもなって私は何をやっているのかというと狂気のマッド黒魔導師をやっております  にほんブログ村
KDDI、au絵文字をドコモと統一 「同じ絵文字で他社とメールを」
「  ←コレ。」 ←コレ。」「え?なにそれ絵文字?全角二文字分くらいなくない?っていうかなんかこの絵文字、黒目なくて、怖いよ?」 「あ、ごめん。そんな怖い印象だった?俺のはクロメちゃんとあるんだ。たぶんキャリアが違うせいだな。アクセシビリティに気を配る余裕がなくてさ><風邪治ったらちゃんとgifで送るから!」 「え、もしかしてこいつ・・・動くの?」 「?!動かない絵文字なんてカザリ  じゃね?」 じゃね?」「俺エロいからよくわかんねーわー」 「  」 」「お前は俺かっ!」 クロメちゃんを擬人化して彼女にするんだ!  にほんブログ村
うーん・・・実に煩わしい・・・
 ニャルラトホテプ星人のニャルラトホテプさんに一目惚れ! ニコチャンで見てるんですけど、コメを見ると心が痛むので見ないっくらい切実ですよ・・・! 今まで聞いてきた阿澄佳奈さんのキャラの中で、もしかしてニャル子さん いやいや僕が惚れているのはあくまで外の人 ゆのっちやぽぷらちゃんが見たら失神したり泣き出したりしそうなあの性格・・・! 極度な貧乳ではないところも、主人公に敬語なところも それでいてちょっとずーずーしいところも、公私混同したりしなかったり 頭をフォークで刺されても一途なところだったり どこに惚れたのかわからないけどニャル子さんにハマった! あー!八坂くんその役僕に代われ! 僕なら最初からクライマックスでデレるから! っていうか八坂くんは女の子!そうに違いない! ニャル子さんは極めてノーマルな性癖の持ち主であろうから 八坂くんがまひろさんで八坂さんだって気づいた時点でメタな方向への一目ぼれに切り替えてくれるはずだそうに違いない! 八坂くんよりもうちょっと下の位置に手の甲ツッコみますから!まじお願いします そして僕はニャル子さんを勝手に脱がした画像を勝手に拝ませてもらう! 本体や本性なんぞどうでもいい! 今見えているニャル子さんがすべてだ! しかしフォークがどこに刺さっているのか、ちゃんと頭なのかどうか確かめたいっ! きっとニャル子さんだからどこに刺さっても平気なのだろう ほてぷはかわいいなぁ 俺の妹超かわいい! ところで地球の娯楽→日本の娯楽なのはまあよくある話なんですけど なぜか成恵の世界を思い出しまして、だって惑星ニッポンっすよ? もうどうせ架空なんだから、鎖国していた日本に、外国人が日本の文化目当てで攻めてきた って設定でもよくね? まあそしたら倒された外国の怪人はどこへ行くのかって言われたらまあ・・・ デジタマに帰るんですよ、うん いやなんでもないです (」・ω・)」うー!(/・ω・)/にゃー! こいつは (’ ’)ノ ちっちゃくないよ! 同様 変換候補に入れたりIDの枠に入れたりして重宝しよう  にほんブログ村  分量が短いせいか、苗字も名前も普通すぎるせいか、ゆるめと松吉以外のキャラの名前が覚えられない>< サエはなんとかわかるのです。 あれです、サクシャンがひだまりのさえ太に対抗しておっぱいを大きくしたとか そんなわけはねーと思いますが、そういう感じで覚えてます^^ なんなんすか相田とか川野とか田中とかくみとか! あ、くみの覚え方発見! 松ミライUさんが中に入ってるのがくみさん!よっしゃこれでおk! くみさんから放たれるすさまじいまでのチャノハタタマミ(まほらば)臭・・・! そしてOP詐欺から感じ取れるすさまじいまでのドッコイダー臭・・・! きっとそういう連想をするのは僕だけでいいって感じもしますが!!!1 ゆるめいつ3でぃを見ていると、冒頭のコメのほとんどが「めぞん一刻ドー・うぃっしゅ!」 めぞん一刻は世代じゃないのでわからないんですが つまりそのようなアパートメントコメディは昔からあった というわけですね。 そうすると、まほらばでいうチャノハタタマミキャラっていうのが既に出来上がっていた可能性も無きにしも非ずということですか チャノハタタマミはすげーっすよ・・・ 中の人ほっちゃんですからね・・・ 当時はまだほっちゃんったらヒロインの座から揺るがない印象があったのに いまやヒロインから犬ネコを経てBBAまでそつなくこなす 黒歴史が全然サジェッてこない声も顔面もたぶん性格も八方美人ですからね なんであんなに天使なんすか! 刑事の勘がこう言っていますよ・・・「筋が通り過ぎている」と! まあそんな黒いものはあったとしても そんなわけで、もう少しゆるめいつの知名度が上がったところで サエさんの全裸画像をあさることにします`・ω・´ だって今探してもあんまり見つからないんだもん。 松吉ロボがぶっ壊れて自分のこと「余」とか言い出したらいいのにw  にほんブログ村  「前回までの仮面ライダーメテオは」 なーんていうからフォーゼのコレジャナイ最終回の夢見ちゃったじゃないですかぁー>< 仮面ライダーフォーゼは、宇宙をモチーフとしながらも地球の、それもほとんど1つの高校でのみ怪人が現れる超スケール等身大の仮面ライダーである ことを踏まえて! 最終回、それも2回分がー・・・ まほろまてぃっく~もっと美しいもの~ばりのコレジャナイ最終回にぃいいいい まあ決して嫌いではないんですがー・・・ フォーゼこと如月弦太朗がホンモノの宇宙人に拉致られて・・・ 「君をこの銀河連盟に連れてきたのは、君の命を救うためだったのだ。仕方がないとはいえすまないことをした。責任はすべて私が取る」 弦太朗「あ、ありがとなおっさん・・・」 宇宙人「銀河連盟で君を治療し次第、すぐに地球に返すことを約束しよう。ただ・・・少し時間がかかってしまうのだ」 弦太朗「それくらい、どってことねえぜ」 宇宙人「地球時間で10万年かかってしまうんだがそれでもいいか?」 弦太朗「10万年!?」 宇宙人「あ、そういえば地球人の寿命はとても短いと聞いていたんだが・・・なんだ、その、2桁しかないんだって?それだと船内時間でも君の寿命が尽きてしまいそうなんだがどうしようか」 弦太朗「なんかよくわかんねえけど・・・どれくらい・・・かかるんだ?」 宇宙人「500年だ」 弦太朗「えええええー!?」 宇宙人「寿命を延ばすかね?」 弦太朗「いや・・・俺は・・・俺の道を進む!」 宇宙人「ハァ!?・・・しかしそれだと銀河3丁目の病院にすらたどり着けないぞ!」 弦太朗「どうしてその話を地球でしてくれなかったんだぁー・・・知っていたら俺は地球で安らかにry」 宇宙人「この惑星の住民はわけがわからん。グビッ」 弦太朗「ガバッ!助けてー!メン!イン!ブラーック!!」 宇宙人「ビクッ!・・・なんだ寝言か・・・」 フォーゼって黒地に白やった?白地に黒やった?  にほんブログ村
最近数学ゴリ押し気味ですみません^^おはようございます量子きのこです
さて、ベクトルの内積と外積というものを数学で習いましたよね そのとき、2つの積の定義を習っても、意味合いがよくわからなかった人は多かったのではないでしょうか ベクトルA(xa、ya)とB(xb、yb)があって 内積A・Bと、外積A×Bというのは具体的に何を意味しているのでしょうか。 内積A・Bの定義はこうでした。 A・B=xaxb+yayb そして、それはベクトルA、Bの絶対値|A|、|B|と、AとBのなす角θと A・B=|A||B|cosθ という関係がありましたね。これはどういう意味なのでしょか。 エクセルを起動して、オートシェイプで適当にベクトルを2つ、描いてみましょう 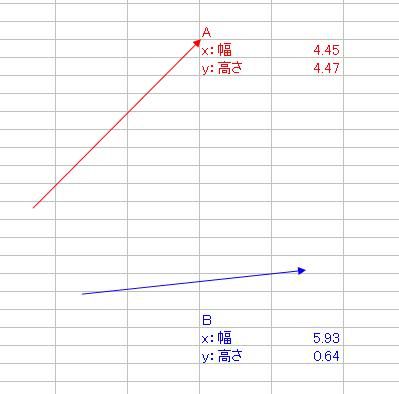 次に、Aベクトルは赤、Bベクトルは青、と色をつけておきましょう ↓ AとBベクトルのサイズをメモしておきましょう 僕の場合は ・A x(幅):4.45、y(高さ):4.47 ・B x(幅):5.93、y(高さ):0.64 とりあえず内積を計算します。 xaxb+yaybなので、僕の場合は4.45・5.93+4.47・0.64=29.2493くらいになりますね それから、とりあえずそれぞれの絶対値|A|と|B|も計算しておきましょう。 絶対値の求め方は、三平方の定理から |A|=√(xa2+ya^2)、|B|=√(xb^2+yb^2) でしたね。僕の場合はそれぞれ |A|=√(4.45^2+4.47^2)≒6.3074くらい |B|=√(5.93^2+0.64^2)≒5.9644くらい それでは、内積A・Bを2つの絶対値|A||B|で割ってみましょう。 A・B/(|A||B|)≒29.2493/(6.3074・5.9644)≒0.77794 これが、実はAとBのなす角度θのコサインだという関係がありましたね。 そこで、AとBのお尻同士をくっつけます。 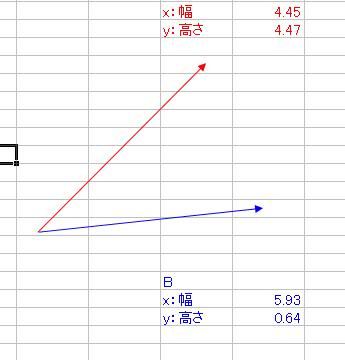 それから、角度を測るために、真四角をベクトルのお尻に添えます。 真四角を少しずつ回転させていって、ベクトルBのお尻にくっつけます。 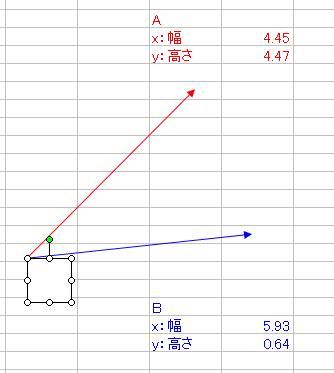 → →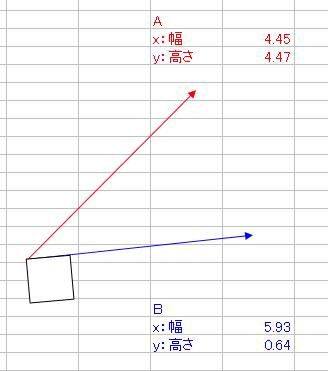 そのときの角度、僕の場合は355度が、Bの角度です。 次に、真四角を複製して、Aのお尻にもくっつけて角度を測ります。 僕の場合は315度が、Aの角度でした。 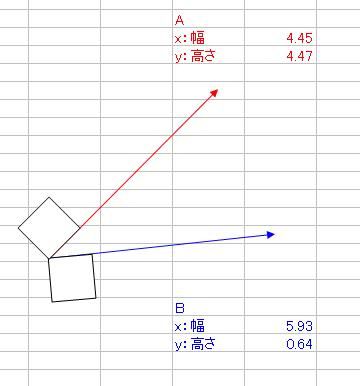 それでは、AとBの角度の差はいくらでしょうか。僕の場合は355-315=40度ですね。 これをθとして、cosθを求めると・・・(※ただし、コサインに入れるのはラジアンに限る) cosθ≒0.7660くらい 精度は悪いですが、0.8近い0.7で、内積A・Bを絶対値|A||B|で割った値とだいたい合ってますね! ======= 次に、外積の意味合いを説明します。 AとBの外積A×Bはxayb-yaxbでしたね。 これは何を意味するのでしょうか。 ベクトルAのお尻をベクトルBの頭にくる  ようにコピーしてから平行移動させてみましょう。 ようにコピーしてから平行移動させてみましょう。同様に、ベクトルBも、お尻がベクトルAの頭にくる  ようにコピーしてから平行移動させてみましょう。 ようにコピーしてから平行移動させてみましょう。平行四辺形ができましたね。 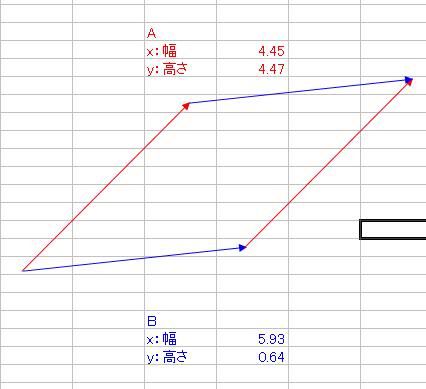 外積A×Bは、実はこの平行四辺形の面積です。 平行四辺形を長方形に変形させて、確認してみましょう。 左側のベクトルAから、水平に線を引きます。 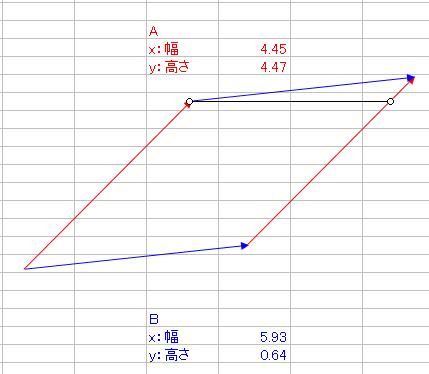 この水平線を、元々のABのお尻に合わせ、 ベクトルAの傾きをそのままに、下の水平線から生えさせます。 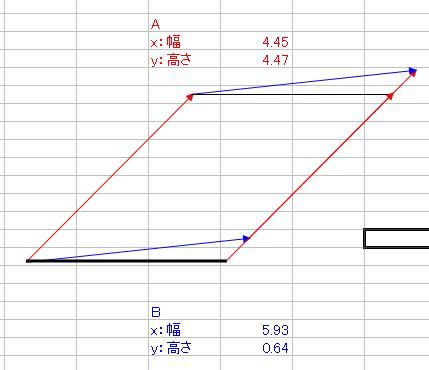 → →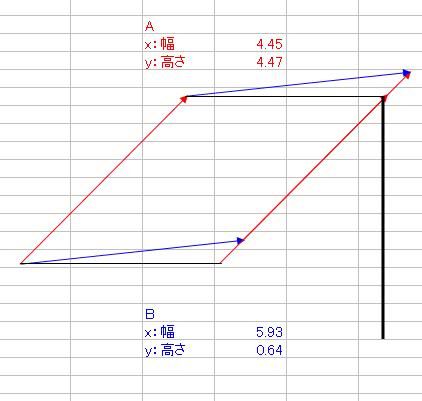 → →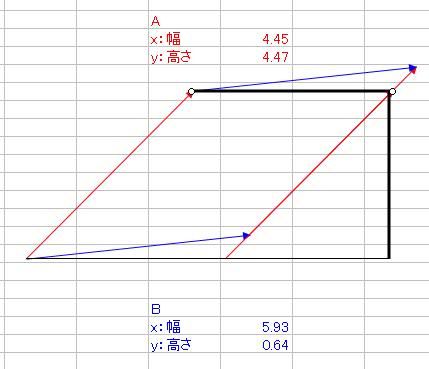 次に、上側の水平線の右側から、 下側の水平線と垂線の重なるところまで垂線と ここで、垂線と上側の水平線の長さをかけたものが、平行四辺形の面積になるので、 長さを測ると、 A×Bと比較しますと A×B=23.6591くらいと、だいたい合ってることがわかりますね。 ただ、A×Bをそのまま計算しますと、マイナスの23.6591になっていることがわかります。 このマイナスは何を意味するのかといいますと、AとBのかけた順番を意味しています。 B×Aの符号、といいますか向きはA×Bの符号と逆になります。 どういうことかといいますと 外積はベクトル積とも言って、スカラー積つまり内積のA・Bとは違って、計算されたものがベクトルになるんです。 一見スカラーのように見えるのは、平面内で外積をやっているからで 画面の手前から奥、あるいはその逆に向かっている成分だけがスカラーのように計算されているだけなのです。 外積A×Bの意味するところは 大きさはAとBが作る平行四辺形の面積 向きは、A×Bとした場合は、AからBに向けて回転する向きと右ネジ(右手)の関係の方向 というものなのです。 今回はA→Bが時計周りだったので、ネジを右に回したら奥に進むように 画面の手前から奥に向かうベクトルとなりました。 ではどうしてこれがマイナスを意味するのかというと 座標系の定め方(約束事)が関係してきて 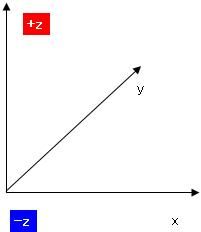 x軸からy軸に向けて回転する方向と右ネジ(右手)の関係に、z軸のプラス方向を定める と公に約束しているからなのです。これを右手系と言って、 z軸の±が逆向きの左手系よりも右手系のほうを一般的には多用します。 今回の外積は、z軸のプラスの向きと逆向きだったので、外積がマイナスの値になったのです。 ちなみに 3次元空間でベクトルA(xa、ya、za)とB(xb、yb、zb)の 外積をする際にはx、y、z軸の単位ベクトルi、j、kと、 行列C=
A×B=|C|と、効果的に覚えられます。  にほんブログ村
夕方の5時6分だったんですけど
トイレで506って数字を見て 11の倍数だなって思って実際に11で割ってみたら46で さらに2で割ったら23で じゃあ506=22×23じゃんかってなって 22と23の平均は22.5だから、x^2-a^2を考えると 506=(22.5+0.5)(22.5-0.5)=22.5^2-0.5^2だなってなって じゃあ506に0.5^2=0.25足した506.25のルートはホントに22.5になる!? って電卓に入れたらちゃんと22.5になるし! それくらい好調だったんですよ^^ でも506.25と22.5が9で割り切れる(倍数ではない)とこまでは視野に入ってなかったー 所詮寝ぼけた頭なんすね!(506.25は81で割り切れますしね) あ、そういえば下3桁625の整数って625=5^4の倍数じゃないですかぁー  にほんブログ村
風車で独楽かよwww
おもちゃにしやすいなwww ・・・ん?風車で独楽? 風車で、独楽・・・? あ。 回転によって姿勢を維持しながら風を地面に吹き続けて浮上するプロペラなジャイロ・・・ 天空の茶色ジュピラかっ! 回転を維持させるには外部から力を加えればいいが 磁気浮上してるわけじゃないので磁石を使って普通のモーターのように回転を与えることが可能。 ※ただし、大気のある環境に限る。 元祖フライングヒューマノイド  にほんブログ村
ここ最近、循環参照ゴリ押し気味ですみませんが、マイブームなので生暖かい目で見守ってやってくれれば^^;
まずは、速度の1乗に比例した空気抵抗を受けながら落下する物体(質点)の運動をシミュレートしてみましょう 運動方程式はこうでしたね。 F=ma F:力、m:質量、a:加速度 加速度aを速度vの時間微分としてみますと a=dv/dtなので、運動方程式は F=mdv/dt になりますね。 では力Fはどうなるかといいますと、今回は速度の1乗に比例した空気抵抗を受けながら重力落下するという条件なので、 速度の向きを鉛直下向きに取って F=mg-rv となりますね。g:重力加速度、r:空気抵抗 ですから、運動方程式は結局 mdv/dt=mg-rv となります。 しかしながら、これではエクセルさんが困ってしまうので、微分を差分に翻訳してあげましょう。 dv→Δvなので、v2-v1 dt→Δt つまりdv/dt→(v2-v1)/dtとなるわけです。 これを運動方程式に当てはめますと m(v2-v1)/dt=mg-rv2 になりますね。 これをv2についての式にまとめなおしますと v2=(v1+gdt)/(1+rdt/m) になります。  これを、図の速度vのところに入れてやります。 v=IF(sw,(v1+gdt)/(1+rdt/m),v0) sw:初期化スイッチが0(オフ)のときはvの初期値v0を維持し 1(オン)になったら循環参照を開始して vのセルに(v+gdt)/(1+rdt/m) を代入する、という意味です。ここでvは自分自身のセルなので循環参照しています。 循環参照を開始する際に、ツール→オプション→計算方法→反復計算にチェックを入れ 反復計算回数を1にしておきましょう。変化の最大値はデフォルトの0.001で構いません。 dt=0.5、m=100/g(mg=100)、r=1、初期速度v0=0としておき 反復計算開始スイッチswを一旦0にしてから1にして、delでも押しっぱなしで再計算し続けると  速度vが0から終端速度vlast=mg/r=100に漸近していくのがわかりますね、わかります^^ ========= では次に、2階の微分方程式に挑戦してみましょう。 力が距離に比例する振り子を例に取ります。 運動方程式はmdv/dt=Fでしたね。 今回このFは、距離xに比例してxとは逆向きに作用する力ですので F=-kxと置くことにします。 ここで、距離という変数が出てきたので、速度と距離の関係を使って距離を定義すると 速度は距離の時間微分なので dx/dt=v でしたね。 この2本の連立微分方程式 dx/dt=v mdv/dt=-kx を差分の形で解くことが 2階の微分方程式d^2x/dt^2=-kxを数値解析で解くことに相当します。 dx/dtも先ほどと同様に微分から差分の形にすると (x2-x1)/dt=v2 の形になるので、x2の式にすると x2=v2dt+x1 になります。 運動方程式F=maのほうも差分化しますと dv/dt=-kx2/m が m(v2-v1)/dt=-kx2 になるので、v2の式にすると v2=-kx2dt/m+v1 になります。 下の図の時間刻み幅dt=0.1、質量m=1、比例係数k=1、初期速度v0=1、初期変位x0=1 として、 変位xと速度vにそれぞれ x=if(sw、vdt+x、初期値x0) v=if(sw、-kxdt/m+v、初期値v0) を意味する循環参照を施してやってdelボタン押しっぱなしとかで再計算し続けますと、 速度と変位がいつまでも往復する様子が描けると思います。 ちなみに、k=m=x0=v0=1にそろえて v-x(速度:縦軸、変位:横軸)をグラフにして、 先ほどの空気抵抗のとき同様、循環参照初期化スイッチ(sw)を一旦オフ(0)ってからオン(1)にしますと 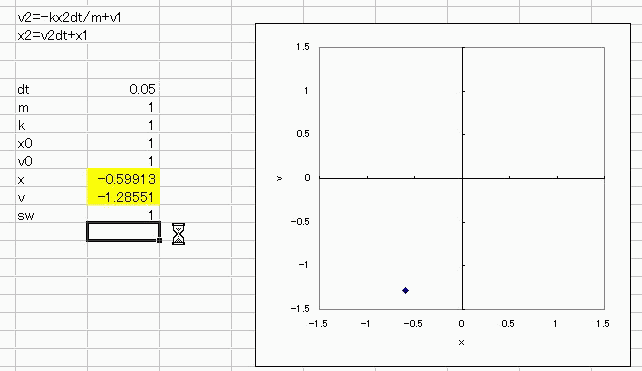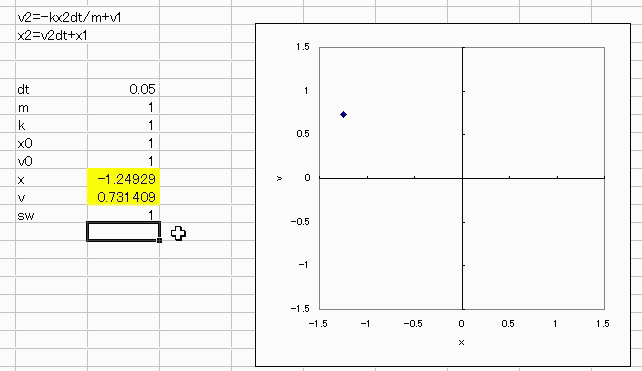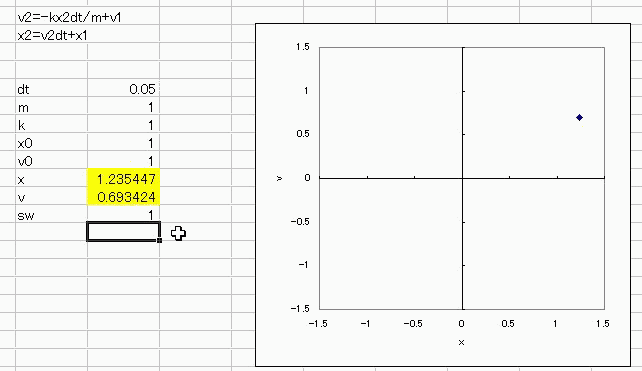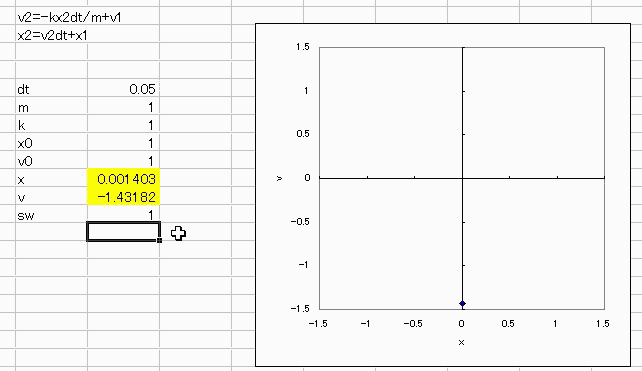 半径約 宇宙キターーー!!  にほんブログ村
キーンコーンカーンコーン
よくエクセルで、シート間の集計を3D串刺しとかって言ったりしますけど そうすると4次元目ってなんなんだろう?って思うじゃないですか。 そこから、そもそもエクセルに4次元なんて概念存在するの?って疑問が湧いてきて しばらくは「やーせーぜー3次元空間だろー」 って思ってたりするんですけど ところがどっこり20世紀初頭! エクセルの4次元目は現実と同じ、時間だったんですよ! 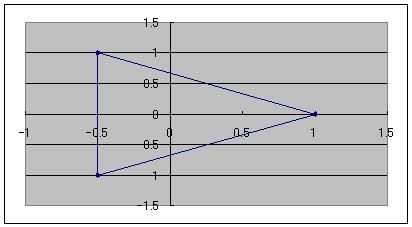 たとえばこんな三角形をグラフに書いたとしますよ。 それで、この3点をランダムに動かすとします。  そうするとこんな感じで記述する感じになりますよね、普通は。 三角+ランド() 3点のx、yそれぞれにrand()関数を足して、delボタン押しっぱなしで再計算すればいいっすよね 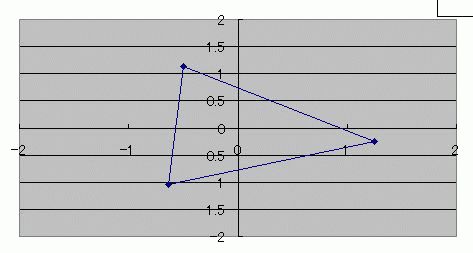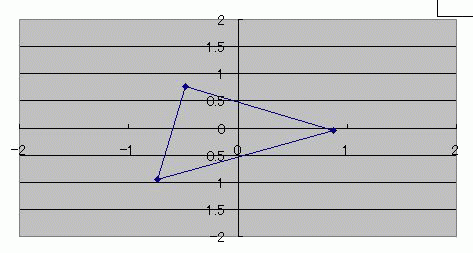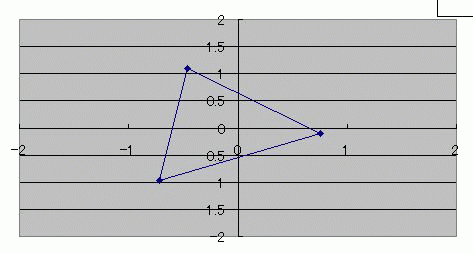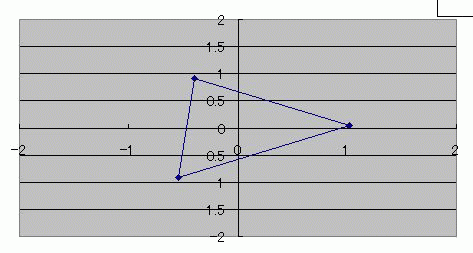 でもこれだとランダム幅をどんなに変えても、この辺界隈をうろついてるウゴツール的な感じを抜け出せないんですよ ブラウン運動には程遠いじゃないですか! そりゃあブラ云々道させようと思ったらできないことはないですよ!  こんな風に見たいコマ別に表とグラフを作って、視点を次々動かせばいいですからねえ できないことはないです。 けど!けど! それじゃ容量食うじゃないですか!ちょっとだけですけど! でもそんなのやっぱ嫌じゃないですかヒトとして、ホモ・菜p園スとして! そこで循環参照の出番っすよ!  三角+ご自身+ランド() これでOKっす! たったこれだけっす! 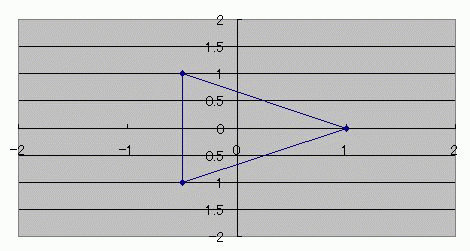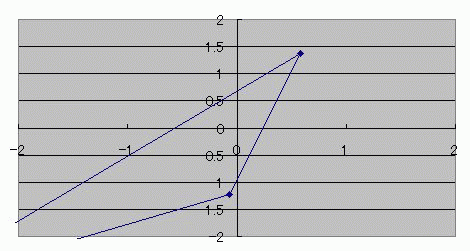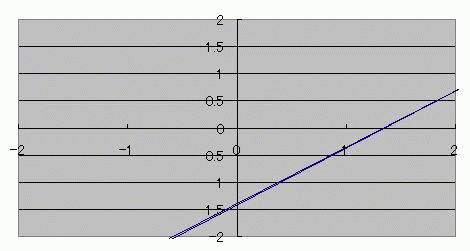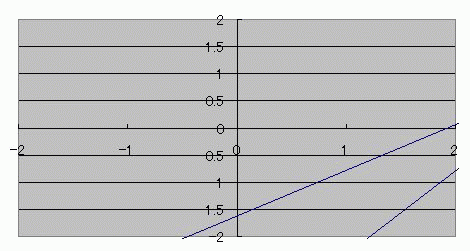 ほら、いつまでもどこまでもうろつけるじゃないですか! 循環参照はプログラムでいうfor文、つまり繰り返し命令のようなものなんす 行は縦、列は横、シートは奥行きって感じで空間的には繰り返しなんですけど 循環参照は時間的に繰り返しなんすよ そしてこの時間には空間のような制限はないんす つまり、この宇宙はエクセルでシミュられてたんですよ!!!!1 ====== ところで、宇宙が有限なのに果てがないっていうの 空間的には合わせ鏡とか万華鏡とかで理解できそうですけど 時間が有限なのに果てがないってどうやって理解すればいいんすかね? それホントに有限なんすかェ・・・? もし無限だったら・・・ただ事じゃおかねえっすよね! そんなのってあるんすか! 数学はさておき物理の世界に限って無限って!!1 ホントは無限が出てこないように宇宙に含まれるエネルギーが限られてたりするべきなんじゃないんすか!? ダークマターも!ダークエネルギーも! 幻なんじゃ ないんすか!! 実は我々は宇宙の3%しかわかってなかったんだよ って、具体的な数値でマニフェスって、人類をちっぽけに見せようとするインペーくんとコーサくんなんじゃ ないんすかーーー!!1 ナンチャッテ 宇宙・・・それは、無限のコズミックエナry  にほんブログ村
ちょっと古い話
 おととしくらいに、コサインボルトのダジャレを具現化する方法を考えたんだ。 I(t)=Ic・cos(φ(t)-π/2) =Ic・cos(∫V(t)dt/Φ0-π/2) これの、I(t)に抵抗でもかましてRI=Vとかってしたらさ (V)=cos(V) フォッフォフォッフォフォー みたいなヘンな式ができそうじゃんか。 これをVについて解きたかったらどうするよ? V=√(V+1) とかだったらな、単に両辺2乗して2次方程式解けばいいだけの話だし cosV=a だとしても逆関数使ってV=Acos(a)ってすればそりゃぁ解けるけど cosV=Vは自分自身とイコールだからなぁ 2分法でも使って数値解析しないと解けないんじゃね? つうわけで循環参照の出番キマシタヨー ======= 方法 1つ目の表 F4:循環参照開始スイッチ(オン:1、オフ:0) F5:Vの上限初期値→1 F6:Vの下限初期値→0 2つ目の表 D列:V 上からそれぞれ上限、下限、中点 中点=average(上限、下限) E列:cosV→cos(D列) F列:2分法の判定符号。V-cosVの符号。sign(V-cos(V)) 循環参照部分 D9=IF(F4=0,F5,IF(F11=F9,D11,D9)):上限のsign=中点のsignなら中点のVを採用、≠ならV上限を維持 D10=IF(F4=0,F6,IF(F11=F10,D11,D10)):下限のsign=中点のsignなら中点のVを採用、≠ならV下限を維持 ※ただし、循環参照スイッチがオンのときに限る。 循環参照がオフのときは初期値(上限、下限それぞれF5とF6)を保つ。 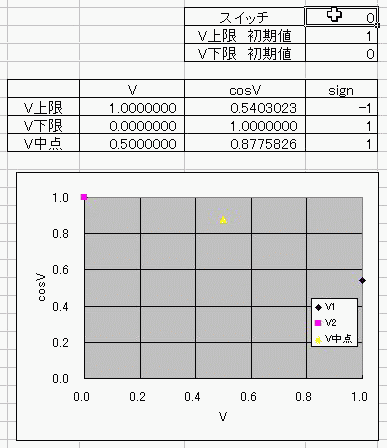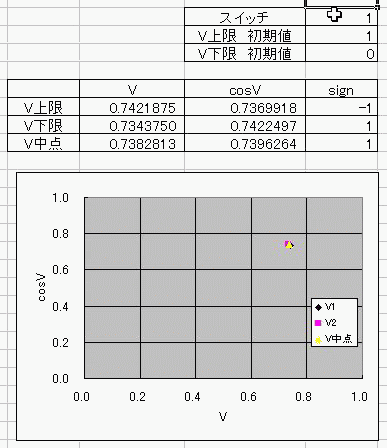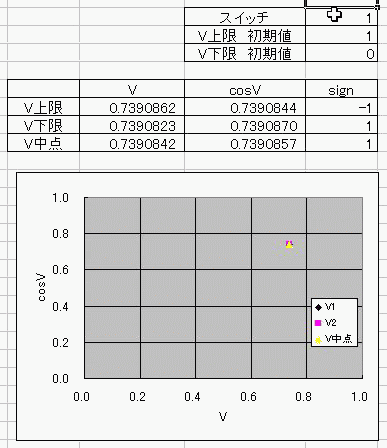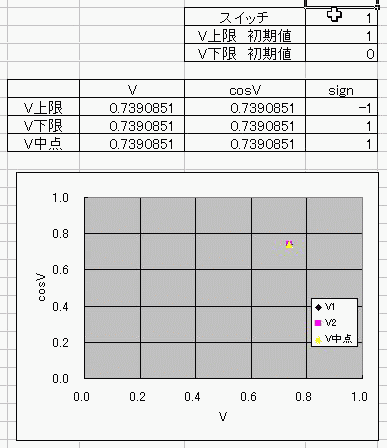 ====== だいたい0.74rad(42度くらい)でコサインボルトはボルトだそっすよw  にほんブログ村 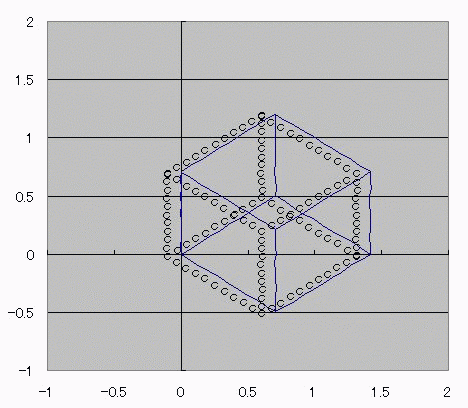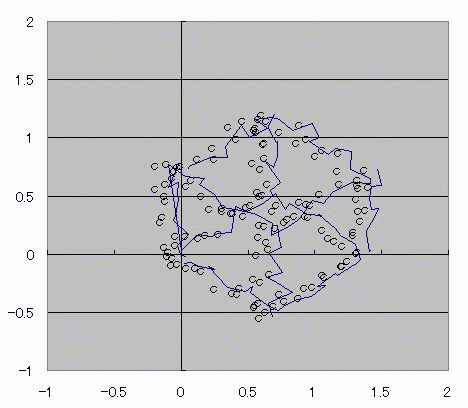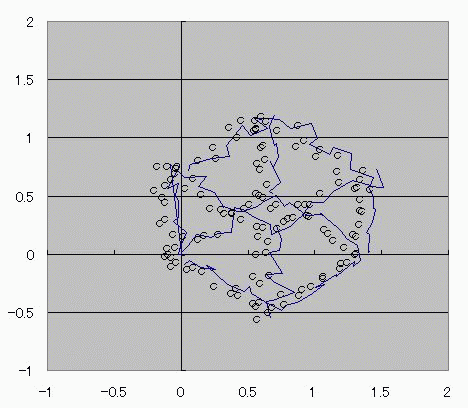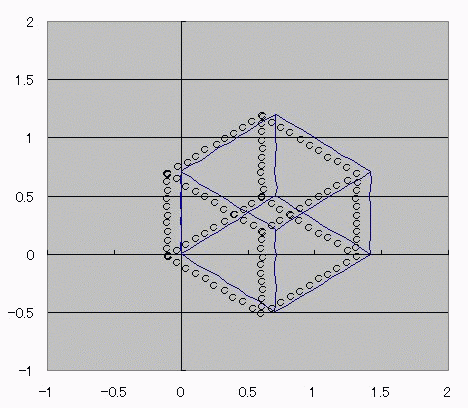 このアニメーションの作り方を使って、循環参照のイイトコロ宣伝を日記にしようと思ったんだけど なんかこう最近は妙に意欲が中途半端でね>< たぶんあれだ きばって書こうぜとか思ってるから1日おきとかになるんだ。 もっとこう、書きたいことを素直に書けばいいんだよな。ブログなんだし。 日記をきばって書くのからさぼって、現実逃避のためにまだやってない計算に手を出してみたりして 本末転倒のようなそうでもないような 昨日はガンマ関数の複素化に手を出してみたりしてた。 前に、4次元とか5次元とか、色んな次元空間における「球のようなもの」、「超球」って呼ばれるものなんだけど その超球の表面積と体積についてブログに書いたことがあって ガンマ関数の概念はそんときにwikiで見つけたんだよ。 階乗を整数から実数、複素数に拡張したものなんだけど それを使えば整数次元じゃない場合の球の表面積が出せるんだ。 実数次元ですらなくてもいい。 たとえば僕らのいるこの宇宙の万有引力の逆2乗則ってのが 実は精密に測ったら微妙に距離の2乗ではなくて2.1+0.1i乗に反比例してたとしたほうがつじつまがあうってなったら この宇宙の空間は実は3なんて整数の次元じゃないかもしれない。 そういうSSを書いたこともあった。 それをもっと具体的にリメイクするために、ガンマ関数の複素化が必要だったんだ。 でも複素積分とか周回積分とか、線積分とか 複素ガンマ関数に必要な周回積分のところでつまずいていたんだよずーっと。 で、季節も春になったしちょっと余力出してガンマ関数のwikiでも見直してみようか って見てみたら、周回積分回避できるっちゅうオチで・・・orz そんでまあ作ってみたんだよ相変わらずマクロなしで。 こんときのためにアドインしといたエクセルの複素数対応機能とか全然使わなかったし でもどういうわけか、精度がせいぜい有効数字1桁なんだよなぁー もっともっと繰り返しが必要なんだろうか・・・ っていうかここでこそ活かすべきなんだよな、循環参照。 そういやガンマ関数の計算方法見てたら オイラーの定数ってのがあんだよ! ネイピア数eとは別の! >超越数と予想されるが、無理数なのか有理数なのかすらはっきりしていない って!ちょー! まあ、超越数かどうかの判定だもんな・・・仕方ないな あれ?無理数かどうかの判定じゃんこれ。 やっぱおそろしいわー無理数。 π+eはどうも無理数ってことはわかってるらしいけど 超越数なのかどうかははっきりしてないらしいし。 超越数っていやぁ チャイティンの定数Ωって超越数を知ったのが3年くらい前だったか 定義もしっかり存在するのに計算不可能な数が存在するって。 雑誌で立ち読みしてたんだけど そんときは理解に苦しんだなぁー 理解できないっていうか、ホントに理解に苦しむ感じで、理解する気が起きなかったんだよ! あれだ、背徳的なかんじ! ヒマジン犯罪者に対して、その意欲をもっと別の方向に役立てろよって感じる一般人の心境! だってよ 2x+3=0のxを計算すんのに、次の問題で 「xって何回書きましたか?」 って言うんだぜ? しかも但し書きで「※xをaに置き換えたり脳内計算したりしてもムダなのよ!」 ってトドメまでさしやがって。 そんなチート問題解けるかーーー!っつーか解く気起きるかっつーの! 丸々3年は理解する気起きなかったし! でもそんなんにも欲張って手ぇ出す人がいるんだから数学ってのはわけわかんねえ世界だよな、うん そういやすっかり言い忘れたけど、いい忘れたからこそ追記。 オメガ数といえば、エロマエ・エロマエのアニメをパワポで作ったらメガバイト級で収まったりしないかとか考えてみたりしてw でもそういえば動画における音声と映像の容量比重はどうなってるんだろう? よく考えてみると動画の大半は音声でできています、みたいな感じなんだろうか。 確かに、gifとmp3を比べたらmp3のほうがでかいことなんてざらだもんなぁ じゃあ音声を全部ボカロにして、この人の声はこの音源、って感じにすればだいぶ圧縮できるんじゃないか。  にほんブログ村 |
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|





