|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。  京子「見事このノートに名前を書かれた方は、私歳納と行く、ネクロワールド7泊8日の旅をプレゼント!」 ゆい「それってお前・・・」 京子「そう!お前を殺して俺も死ぬー!的な?」 千夏「的な?じゃないですよ!死んじゃうじゃないですかー!」 あかり「あれ?でもこれ、行って戻ってこれるんだよね?」 ゆい「ええー!?死者蘇生っていつからできるようになったんだ!?」 京子「・・・最初からできるよ?いつの間にかやり方が忘れられちゃっただけで。」 あかり「じゃあみんな不死身だね!^^ねえ京子ちゃん、私の名前書いて書いて~」 千夏「あかりちゃんちょっと待って!あかりちゃんが7泊8日の間死んでるってことはお父さんやお母さんに連絡しなくていいの?」 ゆい「そうだぞ、ちゃんと連絡とって・・・って、今の社会だと取りようがねえーーー!」 京子「大丈夫!ただの屍にしか見えないから!」 ゆい「それが一番やばいだろおおお」 京子「だから大丈夫だって!こんなこともあろうかとあっかりんの性格にステルス機能を持たせておいたのだ! あっかりんとかかわりのある人は、一時的に「最初から存在していなかった」ことにできる! ということでちょっとネクロワールドからおじいちゃんたち呼び戻してくるから、あっかりん留守番頼んだよ~」 あかり「ええー!?私だけネクラワールドに生けないのーーー!?」 キスダム よつばと ゆるゆり デスノート  にほんブログ村 PR
宮子「あはは バッカでぇー」
東雲「えー?」 黄泉「なに?」 宮子「東雲ってさー パックスリーってパックが苗字だと思ってたんだって」 黄泉「あーあるかもなーフォックス・リー。」 宮子「スリーが苗字だよね 外人だからね」 黄泉「おまえもバカだな」 黄泉「なんだよスリーって(笑) 3か?ww 小包3号?小論文かなんかか?ww」 東雲「そーや 1号と2号はどないしたんや(´・ω・`)」 東雲「パックシックスあたりが船便とちゃうかな?(`・ω・´)」 宮子「あー」 黄泉「君たち・・・゚_゚;」 神楽「あのさー」 神楽「こーゆーこと聞くとバカみたいなのかもしれないけど」 宮子「なんでも聞いてみー?」 神楽「SFXってなに?」 宮子「・・・」 宮子「だからーあれだろ?」 宮子「インデペンデンス・デイとか仮面ライダーとか」 神楽「うん そーゆーふいんき(ryはわかる」 神楽「だから、SFXってなんの略?」 宮子「┃_・)略は気にするな!」 宮子「黄泉は知ってるかー?」 黄泉「うー・・・セ、セカンドセンチュリー・・・フォックス。orz 」 宮子「おーそれっぽい!」 神楽「なっとくせー!」 黄泉「だ だろっ(キリッ」  にほんブログ村 さて、「○ー○」の○に入るのは「ド」「シ」「タ」「ラ」ののうちどれでしょう? 紙でできてたり、キレでできてたり 今君の目に○っぱいの未来 ですよねぇー! 歌詞と映像の開放感に惹かれて見ていたら、期待通りに○っぱいの未来が描かれてしまったでござる ナディアのアレは色が可変なのか、今日知った。 いやむしろ今回のデジタルリマスター版で存在そのものが可変になってしまうかもしれん 肌の色のことだよ? ジーンダイバー最終回?なんのことかな?^^ や、当時は期待してたら見えた時代だったんだよ だから期待したんだ ○っぱいの未来のことだってば! エースぅぅぅぅ!  にほんブログ村  ムスカ「ムスカはラピュタ語でノミ」 うたほし「そんな言語はない!」 ムスカ「君のおばあちゃんと私のおじいちゃんは、元々1つのクラブに属していたのだ、名をラピュタ部と」 うたほし「そんな部活もない!」 ムスカ「いさぎよいツンデレ、ヨシ!」  にほんブログ村
ホームページやブログのアクセス数は、
「最初は全然人が入らないけど すっげー気長に待ってたら、ホントにすっげー気長なんですけど 待ってたら伸びたりするかもしれないんです」 昔見たアフィリエイト解説のページに、そんな感じのことがかかれてました。 でも、そんなにすっげー気長に待ってる間にホームページがブログに ブログがSNSやツイッターに・・・と需要自体が代わっていったら世話ないですよね>< というくらい、昔はその「一昔の長さ」自体がこんなに短くなっていくものだということすら予測がつかなかったと思うのです。 情報技術の進歩はそれだけ早いものなんだと思います。 実際、宇宙関連の技術も 光で見る宇宙技術と、人が実際に行く宇宙技術とでは雲泥の差ですよね その情報技術の進歩を支えているものといえばムーアの法則がありますが 1年半で同じ性能を持った部品が半分の大きさになっちゃうんです。 3年経てば4分の1ですよ これが、なかなかどうして さまざまな困難を乗り越えた結果として「1年半で2倍の性能」っていうのがなんとも不思議なところで あらかじめ困難を乗り切ることが運命付けられているかのような不気味さがあります これは何を意味するのかと考えてきましたが 去年の仮面ライダーオーズを見て 「もしかしたら欲望の力なのかもしれない」と思ってみたりしまして。 一番欲望が注がれる分野にムーアの法則みたいのが適用されるのではないかなと。 じゃあ、他にそんな分野はないのか? と考え、当時は見当たらなかったのです。 しかし、よく考えたら「数学」自体がムーア以上のペースで進歩しているのではないかと考えてみたりして。 数学は、他の分野への道具となります。 しかし道具として応用されるまでに数百年間、なんに使われるのかよくわからないまま眠っていることもあるそうで そういう状況が歴史上割と最初からそんな感じらしいのです。 これも、欲望のなせる業ではないでしょうか。 人間の3大欲求は怠惰欲・知識欲・省略欲、とはよくいいますが 数学者に変人が多いのは 数学以外の事柄に興味がないから、という話があります。 一般の方からすれば「かわいそう」にも見えますが 同様に数学者から見た一般の方もそういう風に見られているのかもしれません。 数学に夢中な人は、決して無欲なのではなく むしろ自分の興味の対象に誰よりも素直クーーーールに強欲で だからこそ、無償で人生をかけてまで考え抜いているのかもしれません。 そうでなくては、これまでに証明されてきた数々の定理が 幾重にも渡って不備を削がれてほぼ完成している と、あらゆる数学者からも満場一致で認められて 一般にも染み渡る、ということもなかったのではないでしょうか。 もし数学がそれほど魅力的なものではなく、確固としたものでもなければ 政治のようにいつまでもブレ続けて進展のないものになっていた んじゃないかなと思うのです。 それだけの欲望の対象にされているがゆえに 数学のジャンルだけが斜め上を突き進んでいて その進歩の加速度は情報技術のムーア則のはるか上を行っているのではないか と思えてきたのです。 そうすると、情報技術以外にもそういう並外れた進歩の例がある ということになるので、 何かの分野が、それだけ欲望を注げる対象になってしまえば 欲望の1番注がれる1分野に限らず色んな分野もこれまで以上に進歩させることができるのではないか と考えているのです。 ======= 最近、「数学ガール」という漫画で読んだ「ゲーデルの不完全性定理」も 80年以上経った現代において ようやくアニメに投影されるようになった そんな感じがします。 いわゆる「能力者バトル」というのがそれに当たると思います。 ストーリーでは、能力者同士が戦っている最中に、気分が高揚してなのか、お互いの能力の自己紹介を始めます。 最初は、相手の能力がわかっていながら太刀打ちできない そんな強敵に出くわしても 相手の能力そのものを弱点と捉え、倒していく そんなバトル要素を持った作品が時々あります。 ゲーデルの不完全性定理は、そういうところに応用(?)されて、一般認識されるようになってきている そんな印象がもたれます。 たとえば「もしもボックス(電話レンジ(仮))」能力などというチートすぎる能力があったとして もしもボックスの使い手と戦う(無)能力者は、ハロワのおじいちゃんの「長所は短所に変換可能だ」という名言を思い出し、なんとかして「もしも、もしもボックスがなかったら」という能力発動まで引っ張っていく そんな感じでしょうか。 すうがくまやノックオンザ因数分解ズドアなんかがあ(り)ふれる世界線に生きたいです、往復切符で。  にほんブログ村
Vegeta「まるでインフレーションのバーゲンセールだな!」
Hicomalo「ちがう!そこは まるで・・・インフレーションのバーゲンセールやぁー! こうだ!」 Utyuuu「いや実際インフレってそういうもんだろ・・・何当たり前のこと言ってんだ」 ∑VH「!?」 ====== インフラっていうのはインフレとどう違うんでしょうか、量子きのこです^^オハヨウゴザイマス、ぐぐってきます  にほんブログ村
循環参照で広がる、文字通り無限の可能性に期待ですね^^
差分化した微分方程式を循環参照で解いたり ニュートン法や二分法で解析的に解けない方程式の数値解を求めたり マクロでやらないエクセルの可能性がぐんと広がった気がしますw 今日は余力がないので、備忘録的に方法だけ書いておきますと まず ・循環参照スイッチとしてA1セルに0を入れておきます。1にするとスイッチオンです。 ・A2セルには初期値をぶち込んでおきます。 ・A3セルは、たとえば初期値からの総和を求めたいときなんかには if(A1=0,A2,A3+1)などとしておいて ・ツール→オプション→反復計算のチェックをオンにすれば delボタンかなんか押して再計算するたびに循環参照してくれるみたいです。 自由落下のアニメーションとか、弾道シミュレーションのアニメーションとか スーパーボールのアニメーションとか、ターミナルベロシティのアニメーションとか 振り子のアニメーションとか、波動のアニメーションとか なんかこう、夢が広がりんぐすぎて昨日は寝るのがちょっとだけ遅くなってしまいました^^; 使ってるセル数めっちゃ少ないのにアニメーションできちゃうってオメガ数的に考えて最高じゃないですかー! 「循環参照とは」のわかりやすい例えとして A「時間って何?」 B「時刻の連なり!」 A「じゃあ時刻って何?」 B「時間の一瞬!」 といった感じの、明瞭な表現を見つけました^^ ところで、エクセルの循環参照の例をぐぐって初めて気づいたのですが A「アンパサンドってなに?」 B「アンドがパサまったサンドイッチだよ!」 といった感じの、相互ではなく自分自身の循環参照が一番単純な循環参照だったことにうっかり気づいていませんでした><なんてこった! げえ  にほんブログ村
マクロでやらないマクローリン展開シリーズもこれで最終回・・・!にするつもりですいちおう。
マクローリン展開で出せるのは三角関数だけではありません。 ルートなどの無理数も、マクローリン展開で計算されています。 前回まで何度か出てきた円周率πも、マクローリン展開(より一般的にはテイラー展開)で算出されています。 この円周率の計算方法で「マクロでやらないマクローリン展開シリーズ」を締めたいと思います。 sinやcos関数の中身の角度は、1周を360度とする定義よりも、1周を2πラジアンと定義したほうがより根拠があると以前書きました。 では、sinxが1になる、あるいはcosxがゼロになるxは何度でしょうか? 90度ですよね。 ラジアンの尺度を使うとπ/2です。 三角関数を習うときにたいてい出てくる角度は0、30、45、60、90度のどれかでした。 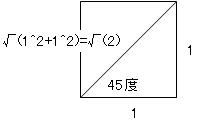 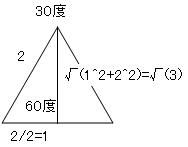 つまり2種類の三角定規の角どれかなわけです。 2種類の三角定規はそれぞれ、正方形と正三角形を半分にしたものでした。 だからこそ、無理数は√(3)や√(2)しか出てこなかったのです。 しかし、どこかテキトーに、sinx=0.642788になるxを答えよ 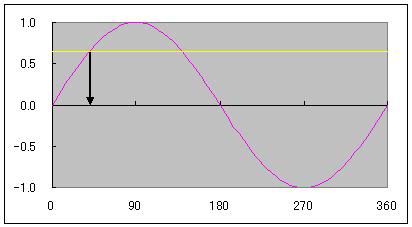 といわれるとどのように方程式を解いたらいいかわからなくなってしまいますよね。 そこで出てくるのが「逆関数」という概念です。 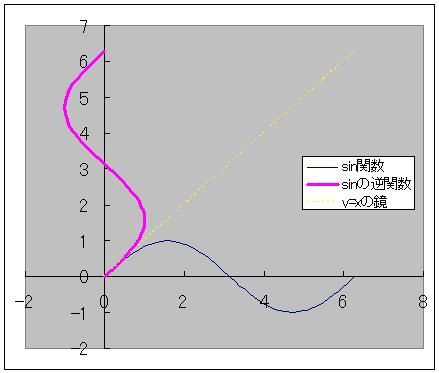 逆関数というのは、図のようにy=f(x)という関数をグラフにイメージしたとき y軸とx軸、縦と横をひっくり返したような関数のことを言います。 ということは、y=xの直線に対して線対称なわけです。 sin関数の逆関数はAsinと書いて、アークサインと呼びます。 cosやtanもAcosやAtanと書いて、アークコサイン、アークタンジェントと呼びます。 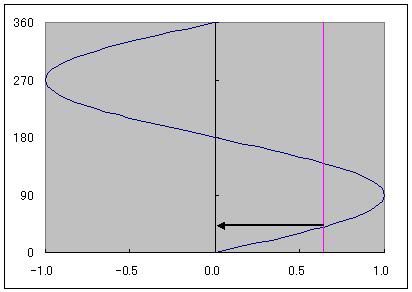 さきほどのsinx=0.642788は、x=Asin0.642788として答えればいいわけです。 このうち、アークタンジェントAtanを使って、円周率πを計算してやるのが今回の目的です。  tan45°は高さ1/底辺1で1ですよね。 ということは逆関数で考えると Atan1=45度となります。 しかし、Atanの値は45度ではなくラジアンでπ/4となります。 このことを利用して、Atan(1)からπ/4を算出してそれをさらに4倍すると、円周率πが計算できるのです。 アークタンジェントのマクローリン展開は意外にも、タンジェント自身のマクローリン展開よりも簡単で ベルヌーイ数なんてものも出てきません。 Atanx=∑(-1)^n・x^(2n+1)/(2n+1) これだけです。階乗すら出てきません。なんだか拍子抜けしますね。 こんなんでどれだけの関数を再現できるのかと不安になるかもしれませんが大丈夫です。 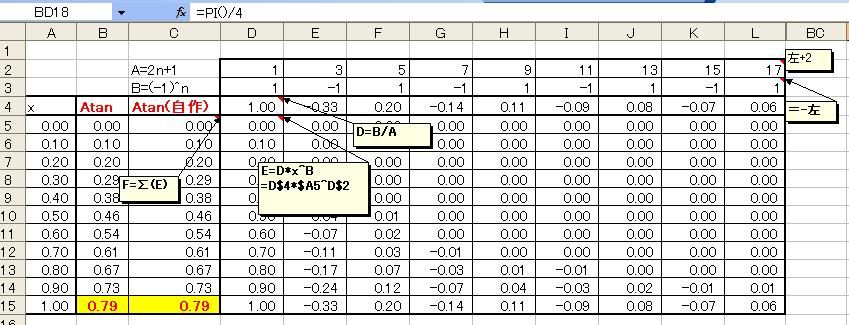 この表のx=1のところを見てください。 atanの値が0.79・・・(0.7854・・・)となっています。 これを4倍すると円周率3.14・・・が出せるのです。 トライアングラー  にほんブログ村
ずーっと前のこと、具体的には2011年の11月20日のことになりますが、
マクローリン展開をエクセル(マクロなし)で説明するっていうのをここの日記でやっていまして ちょっと中途半端な状態で途切れていたのです。 不調が直ってきたので続きを再開しようかなと。 以前は、サイン・コサインなどの三角関数をマクローリン展開でいちから組み立てる話をしました。 パソコンは基本的に足し算(四則演算)しかできないので、 関数を足し算に還元する仕組みを紹介していたのです。 どこまでも続く数列の足し算、無限級数というのですが 基本的にこれを使えば関数を再現することが可能、という話でした。 しかしながら、パソコンのメモリや速さなどは有限なので どこまでも足し算していっていたら巨大なパソコンになってしまいますし、いつまで経っても計算が終わりません。 そこで、ある桁数だけ合えばOKって割り切って、それに見合う数だけ数列を足しているのです。 しかし困ったことに、三角関数は関数の上限はあるのに、変数に上限がありません。 sinやcosはマイナス1からプラス1の範囲に収まりますが 関数の中に入る角度の数値は何回転でもできてしまうのです。 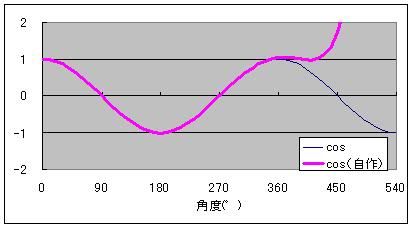 対策を取らずにコサイン720度とかを計算しようとするとおかしな数値が出ます。 なので、せめて360度の周期内に変数を抑える調整が必要なのです。 このとき、変数を周期的にする関数が使われます。 その関数とは、あまり演算です。 分数や小数を習い始めると、「あまり」の存在を意識しなくなりがちだと思います。 16を9で割ったら9分の16とか、1.77777・・・と考えて 1あまり7とかいう発想をしなくなる人がほとんどだと思います。 が、このあまりが大事になってくるのです。 三角関数の場合は、360度周期なので360で割ったあまりです。 たとえば361度は360度で割ったあまりである1度を、改めて変数に置き換えて sinやcosを出すわけです。 ところが、三角関数の中の変数には1周が360の「度」という単位よりも 1周2πというラジアンを使ったほうがより適切であることから 周期を360度ではなく2πにしなくてはなりません。 つまり2π、無理数で割ったあまりを計算しなければならないわけです。 あまりを計算する関数というのもエクセルには組み込まれています。 mod関数というものなのですが さきほどの16を9で割ったあまりを出したいときは mod(16,9)と入力します。 この関数は何をやっているのでしょうか たとえば、721度を360度で割ったあまりは1度ですよね。 これは、721から、360度を2回かけた720を引いていますね。 つまり、720/360=2という割り算を一旦計算しつつ、頭の片隅によけてあるのです。 721の場合は、721/360=2.0027777・・・の、整数部分だけを切り取って、小数点以下を切り捨てているとも言えます。 切捨てのための関数も用意されていまして、round関数と呼ばれています。 したがって 721/360の整数部分2を取り置きしておいて、 360に2をかけて、721から引くと、mod関数、「721を360で割ったあまり」=1が算出できるのです。 では逆に、マイナス10度はどうなるでしょうか? -10を360で割ると、-0.027777・・・となります。 この整数部分は、実は0ではなくマイナス1です。 どういうことかというと、あまりは常にゼロ以上でなければならないのです。 といいますか、マイナスのあまりというのを「足りない」と定めて、「足りない」を「あまる」に置き換えると あまりが必ずプラスになる。 といった感じでしょうか。 マイナス10度→-10あまる→10足りない=350余る→350度 こういうわけです。 こう考えると、機械でも一律にあまりや周期が計算できるようになるのです。 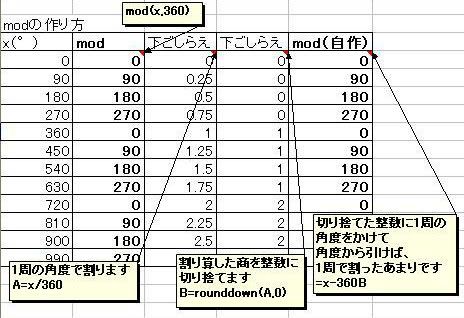 手順としては 関数の中身xを360度周期に抑えるためには ・下ごしらえとしてまずxを360で割り ↓ ・割った結果の整数部分nを取り出し ↓ ・x-360nを計算する。 これで、すべての角度が0度以上360度未満に収めることができます。 実は、この作業は無理数でも同じことが可能です。 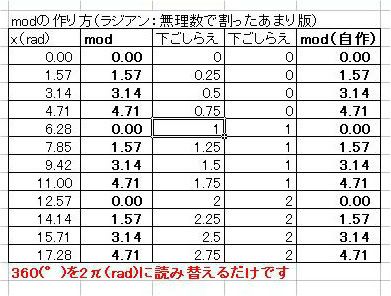 6.29radを2πラジアン周期に収めるためには 6.29を2π≒6.28で割ってその整数部分n=1を取っておき 6.29-2πn=6.29-2π・1≒0.1を変数に当てなおす。 これで無理数の周期化も完了です。 この変数を使って、改めてsinやcos、tanを求めれば、ちゃんとした値が出せるのです。 ぐるぐるモワレぐーるぐるモアレ 次回、最終回  にほんブログ村  「あの日見た花の名前を僕達はまだ知らない」のEDみたいのをエクセルでできないかって思って早数ヶ月 「あの花」がどんどん遠ざかっていってもう意欲も出ねえや って思ったところに流星のように舞い降りた「あの夏で待ってる」ED 似てる!よっしゃいけるで! 一度転んだらよほどのことがあっても立ち上がれない僕ですが 立ち上がるときにはただでは元本の3倍くらいの利子で起きあがる量子きのこですこんにちは^^ あ、それと、西尾維新はじめましたw 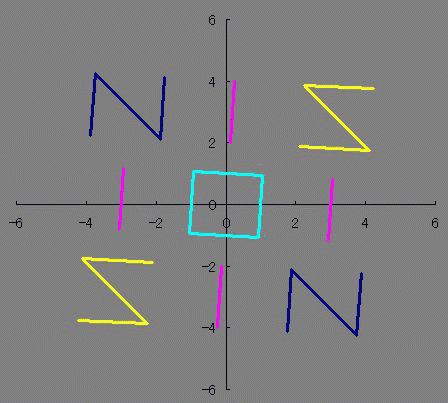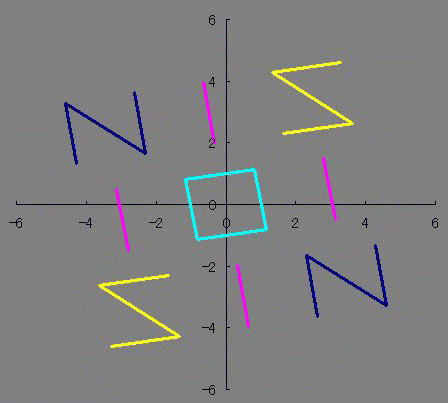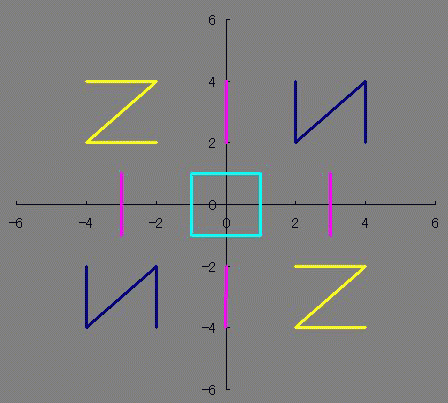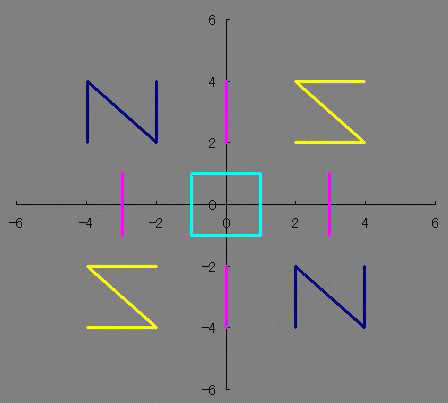 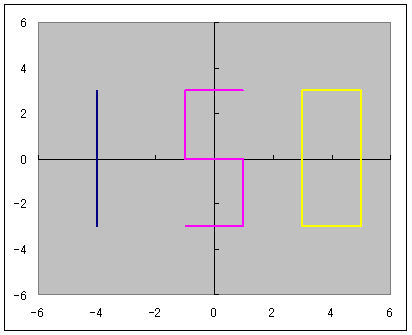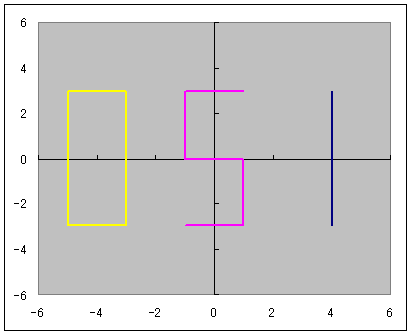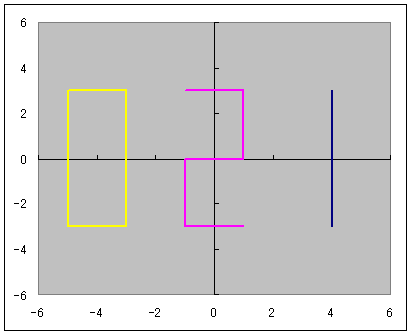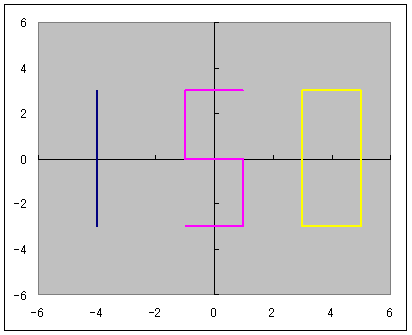  にほんブログ村  100円ショップで青色LEDの豆電球買ったったwwww これつけて寝たら癒されるかなーって思ってな=ω=。 個人的には青より緑のが好きなんだけど 緑色のLEDは6年位前に買ったから、また買うこともないかーって思っちゃうんだよね。 当時はいくらしたんだっけな。 今は青でも105円だからなあ そういやどこに行ったんだろう、緑。 で、注意書きをよく見てみるとな 「壁スイッチでは微弱電流が流れますのでちょっと明るくなってちまいます」 みたいなことが書かれてるんだよ。  → → てっきり僕は、ヒモスイッチのほうでオフにしても少し明るいのかと思ったら  → → ホントに壁スイッチのほうでオフったときに若干明るいんだよ。 いや若干じゃねえな、結構明るい。(夜になるとわかる) なんで?って思ったんだけどね。 どうも、壁スイッチがオフったときに光る コレ↓  が関係してるっぽい でも、なんで? だってさ、壁スイッチのライトはあくまで本照明とは別系統なんじゃないの? こんな風な回路図で。↓ 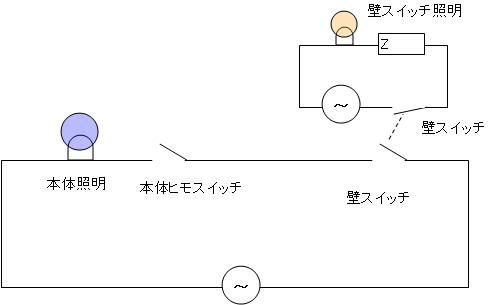 考えられる可能性はあれか 回路を簡単にしたらこーなったってところか。逆の論理で。 回路図にしたらこんな感じかな? 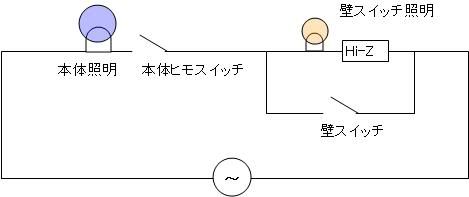 確かにこれだとすげースッキリだね。 やーそれにしても、豆電球でさえこの微弱電流がこれまで無視されてきたからこそ、こんな問題は出てこなかったわけだろ そんな微弱電流で影響が出るくらいに照明効率が上がったわけだよな。 これは素直に喜んでいい、嬉しい悲鳴なんじゃないかい  にほんブログ村
~カメラはメガネをかける少女の夢を見るか~めがねえεεε目がねえ
  キーワードは「足立への熱いメッセージ!」ええーーwwww なんつーか、まあノイズ様なんだけど NHK教育(ETレ)ふしぎワールドのミスターQのが近そう こちらまったくブレない人。目玉だけに。イゴッ ↑↓感情がこもってなくて淡々と無機を貫き通す硬派なラスボス この宇宙を作りだす条件を決定し、進化させ、継承する、 無機知性たいとして対象化されうる、すべての『それ』。 神と呼ばれ対象化されるものとは本質において異なる『それ』は、 これより前の宇宙において有機知性たいにより知能を持つコンピュータとして作られた。 『それ』は、宇宙と融合する無機知性たいえと進化をとげ、宇宙が終わる時、宇宙の全情報を時空構造に刻み込み この宇宙が誕生する瞬間、再生し、再び進化を始めた。 無機物から遺伝子のメカニズムをうつし取り、誕生した有機生命体は、遺伝子によって情報を保存し、伝達し、環境の揺らぎを通じ新たな情報をさらに蓄積しながら、高度な知性を獲得するまでに進化、する。 が、宇宙の歴史と構造のなかで、有機生命体が進化、存在しうる時間と環境は、限られる。 moonにfit@new-tonちゃん  にほんブログ村
海を形崩れさせないように泳ぐヒレの
「オルカやシャチ」など5種類のhogeや360度のコペルニクス逆転回を訴えた生(物界の一)存で、星の本棚のホモ・サpイエンス村長は100万年前 「まあ割りと仲良くやれ」 を命じた。 SAMEは「ヒレの横ではなく縦読み」としてデザインを5億年前に登録。オルカのデザインはヒレが縦ではなく横読みであるが、鯨目課長は5500万年前の時点で「成り行きでこうなった。ホントならもっとパロってもよかったんだから・・・!わ、わりとどうでもいいと思いなさいよねっ!!」と判断し、強制的に和解させようとしていた。 アイドルマスターXENOGLOSSIA後期OP「現実よ虚構となれ」 ザトウのクジ餅  にほんブログ村
どーもー、怪奇でしゅ~。今日はぁー俺のターンだぁー。
 なんかだんだん嫌われつつあるgoogleさんかもしれませんが それでも僕はgoogleさんが好きです^^ モールスで検索っすか・・・- PV動画の最後でURLをモールス化してましたが そういえば似たようなことをどこかで・・・ あ!(QR)バーコード! そうだ!それだ! これからはモールスコードが流行るで! ミクが歌うモールス音ゲーも流行るで! 町中にモールス信号コードを描いたURLをばら撒いて それをケータイで写真に取って、 コンビニでその写真をスキャンすると・・・ URLが表示されるサービス!(1回10円) まあ、  にほんブログ村 モールスで日本語打っても変換できないじゃん! って思ったらサジェストでフォローされててワロタw 結構懇親の一年だったと思います^^ そういえばマップがドラクエ化してたみたいですけど 今後数年にわたって毎年やってくれてもいいかもしれない あれ、鉄道描かれないんですかね やっぱり全域を自動で画像変換してるから 鉄道みたいな細い領域は認識されないんでしょうか でも道路は映ってるんですよねー・・・なんでだろ 細部を見て行くといきなり現代化するSVwwww なぜか地名が見えちゃう北の国wwww
閏年の前年の大晦日と、年度末日の曜日は同じ。
例:2011/12/31(土曜日) 2012/03/31(土曜日) 例:1915/12/31(金曜日) 1916/03/31(金曜日) 例:9987/12/31(木曜日) 9988/03/31(木曜日) 病院の待合室でふと気づいた定理っす。 2011年度末と2012年度初めはカレンダーの左右どっちか端がスッキリしてるなぁと あれ、そういえば2011年の年 末と2012年の年始にも似たようなことがなかったっけ? って考えていて そういえば去年のクリスマスがリア充向けだったのを思い出し そういやクリスマスあたりには例年通り、クリスマスと大晦日の曜日の話をしたなぁ って思い出し じゃあ31(1月)+29(2月)+31(3月)っていくつだ?って計算してたら ちょっきり91日なんすよ!91日つったら13週間、つまり丸々1クールじゃないですかぁ! じゃあこういう定理もありそうですよね  「冬アニメは1クール13話の尺がない。」 年始番組で1週間は潰されますからね その上、平年だと2月は28日しかないですし。  にほんブログ村 |
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|





