|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
そういえば最近はブルーバックスも買わず、紙の本もマンガすらあまり読まなくなって
いつの間にか科学ニュース記事より突っ込んだ話から遠ざかっているような気がしてて 量子コンピュータの制御NOTがどうの言ってたのももう何年も前の話しだったっけなぁとか思いながら まあ進歩がノロマな量子コンピュータだし、まあいっかとか思ってたんだけどまあモグリだわな そういや制御NOT(CNOT)ができてるってことは古典ロジックICで言ったらNANDができてANDもORもNOTもできるよー的な感じらしいじゃん あれ?それってもうそろそろ汎用なんじゃねえの? とか今更ながら思ったりして。 なんかwiki見るといつの間にかプログラミング言語ができてるって? それでも汎用性が低いって言い切ってるのはどういう根拠なんだろう? 単に集積度が絶望的に足りないよ~って意味なのか、絶対的に何かの要素が欠けているのか そんな答えをいち巡回サラリーバイトごときが出せるはずもなく なんとなーくCNOTってXORみたいなんだよね~ とか思いながら、XORからNANDを作ろうとしても何度やってもできない。 NOTはできるんだけど、ANDとORができない・・・
だって2入力真理値表の出力の1の数が偶数なんだもん>< しかもまったくの対称、これじゃ非対称にしようがないじゃん ってwikiを見直すと あれ? そういえば量子計算って根本的には情報増えたり減ったりしないんだよね 入力が2つあったら出力も2本あるはずなんだよね あ、思い出した。 「制御」NOTだもん。制御されてこそなんだよ。
制御入力のAが0なら、制御フラグは立たないよ的な意味の出力Cなんだよな フラグが立ってないから出力Dは入力BのNOTにはならない あくまで1入力のNOTなんだよ。2入力のXORじゃなくてな。 まあ使いようだろうけどさ。 このCNOTが古典でいうところのNANDみたいな感じで コレ1つあれば基本的にはなんでも作れるっていう素子にあたるわけだから じゃあいつから汎用性あがってたの?って話なんだよな。 ってかそもそも何をもって汎用性っていうのよっていう そういえばCNOTでなんでも作れるよーって理屈は古典的に導出可能なんだろうか で、またまた出会ってしまったユニタリ行列
まあ、これはCNOTの行列であってユニタリ行列の一例でしかないんだけど ユニタリ行列の定義はA・A†=A†Aが成立する行列ならなんでもいいんだってさ。 ここでA†ってのが、エルミート共役で、転置した上で要素の複素共役をとったものがエルミート共役。 ttAが転置、kyAが複素共役だったら、tt(kyA)=ky(ttA)=A†ってわけ。 †ってダガー(剣符号)って読むんだってさ。なんかムカツク記号だよねー。 何この人員不足で適当な怪人派遣されてきましたみたいなの。 まあそれで、 複素共役とるんだから、一般には要素が複素数の行列なんだよ で、せっかくだからまた出会ってしまったエルミート共役 そういえばエルミート行列ってのもあったよな そういえばエルミート行列とユニタリ行列の定義の違いをまだ知らなかった エルミート行列はエルミート共役っていうくらいだからユニタリよりも定義が単純?で エルミート前後で一緒、つまりA†=Aならなんでもいいんだってさ。 つうことは具体的に
って感じのn行×n列行列なんだと。 固有値は必ず実数になるらしい。 ってここで、昔は固有値の意義も理解してたはずなんだけど、いつの間にか忘れてしまったので 固有値・固有ベクトルの定義からネットで再勉強中 エルミート行列の純虚数成分を除けば実対称行列だよね。要は転置前後で一緒っていう。 そういう行列の固有値ももちろん実数らしい。 ってことは、わざわざ関数の立体グラフ書いて複素平原で零点を探さなくていいわけだ。 単にx軸とy軸の2次元グラフで解を求めていいって保証がある。こいつはお得だ。 解の重複を除けば、n×n行列の固有値はn個って決まってるわけだし。重複を除けばな! だから、数値解析でなんとかならんこともない! 固有値まではすらすら覚えてるんだが 固有ベクトルがなかなか出てこないのよ つうことは固有値・固有ベクトルがそもそも何なのか忘れてるんだなorz 前からの課題なんだよ・・・エルミート行列の固有値が実数になるっていうのを証明したいなぁーって。 サイト見たら説明がちんぷんかんぷんで参った・・・  にほんブログ村 PR 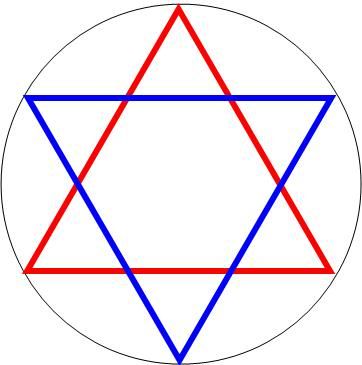 普通、こんな風に2つの三角形を重ねて でも実は、こんな風にウィンドーザーできましてね それと、七芒星以上になると、1つとは限らないんですよ 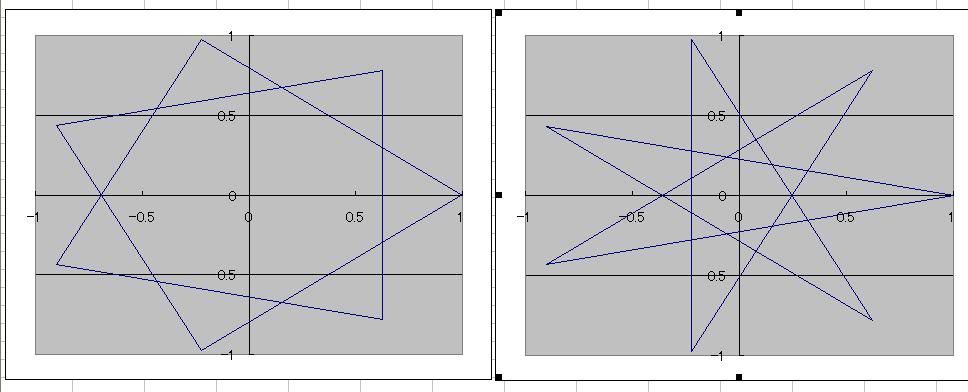 七芒星だったら2種類しかありませんが 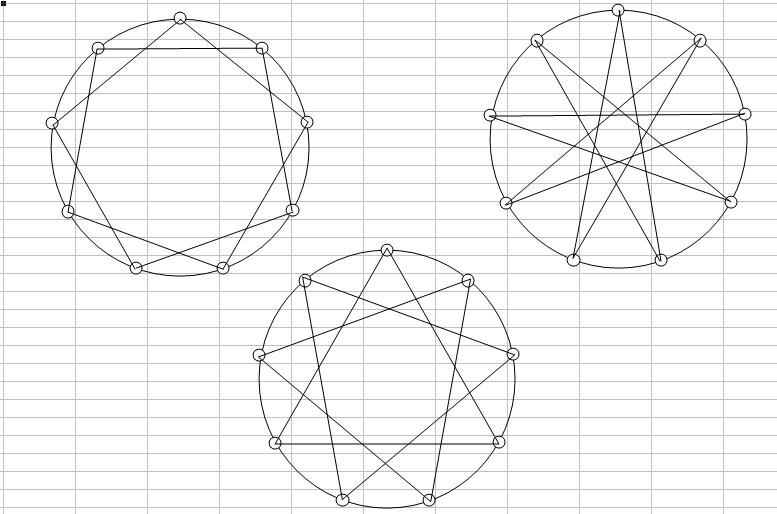 九芒星だと3種類ありますからね 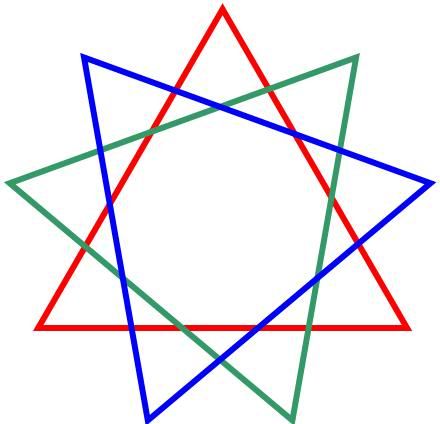 そして、九芒星の1つにはこんな風に三角形3つに分かれるのもあるんですが これも実はこんな風に それと ナントカ芒星ってなぜかimeちゃんで変換できないんですよね~ふしぎな冒険の世界まで未知への空間造るのさ~ あ、そういえばこないだ2997ってナンバーを見かけましてな これ9で割ってもまだ333になって9で割り切れるんすのよ ってことは2997自体は3の4乗つまり81の倍数なんすよね。 なんかこう、完全になる一歩手前で止めて、別分野を極め始めて また極める一歩手前で止めて別分野に興味を出して・・・ ってやるとある程度までの完成度が出来上がるけど、そのさらに上の完成度がゴロゴロいて インフレはどこまでも続き、興味の対象は尽きない そんなテトリスのコンボ技みたいなのが宇宙の真理なのかなぁってちょっとだけ思うましたよ。  にほんブログ村
おいらの公式の両辺8乗とニコ定理から、まずは8倍角の公式を得る
「四半世紀」という言葉があるので、八半角なんてのもいいかと思って名づけてみた。 オイラーの公式の8乗:(cosθ+isinθ)^8=exp(i8θ) ↑何乗かしているときはド・モアブルの定理という(≠ド・モルガン) 二項定理:(x+y)^n=∑(nCk・x^(n-k)・y^k) (0≦k≦n) (ニコ定理:たとえば(x+1)^5=x^5+5x^4+10x^3+10x^2+5x+1 ∑:総和。たとえば∑(k) (1≦k≦5)だったら1+2+3+4+5なので15 nCk:組み合わせ。nCk=n!/(n-k)!/k! たとえば5C3=5・4・3/(3・2・1)=10=5・4/(2・1)=5C2 n!:階乗。たとえば5!=5・4・3・2・1 総積(直積?あ、総乗か)Πを用いればn!=Π(k) (1≦k≦5) なぜか階加(階和?)に相当するものがないので「n?」とでも名づけてしまいたい) 順列・組み合わせと2項定理については過去の日記も参照してくれるとありがたい ↓ 8倍角の公式 :cos(8θ)=128cos^8(θ)-256cos^6(θ)+160cos^4(θ)-32cos^2(θ)+1 cos^2(θ)=xとし、上の式の変形である以下の4次方程式を解く。 128x^4-256x^3+160x^2-32x+1-cos(8θ)=0 4次方程式:x^4+ax^3+bx^2+cx+d=0があるとき q=c-ab/2+a^3/8がゼロの場合は(やっぱりそんな気がしたんだ!) p=b-3a^2/8と r=d-ac/4+a^2b/16-3a^4/256を用いて x=-a/4±√(-p/2±√(p^2/4-r)) という解の公式がある。 q≠0だったら x=-a/4+A/2±√(t0/2-p/4-q/(2A))らしい A=±√(2t0-p) t0は8t^3-4pt^2-8rt+4pr-q^2=0の解の1つとのこと。 4次方程式の解法はほかにもいろいろある。 以下の4つの解が出てくるので(±が2つなので2^2で4つ) cos^2(θ)=1±√(1±√(1+COS(8θ))/√(2))/√(2))/2 cosθを求めるためにさらにルートを取り、以下の8つの解を得る。 (2^3で8つ) cosθ=±√(1±√(1±√(1+COS(8θ))/√(2))/√(2))/√(2) なんとなく連分数っぽい感じがするが、あの日みた連分数の定義を僕はまだ知らない このcosθが8半角の公式である。 用途:cos30°=√(3)/2から、30°の8分の1である3.75度などのcosが得られる。(実際にはほとんど用いられないと思うが、n倍角の公式の使えなさよりは少しはマシかもしれない) ところで、なぜ8つ出てくるのか。 これは、8で割る前のθというのが8つ重なっていると考えられることからきている。 つまり、θ、θ+360、θ+360×2・・・θ+360×7が重なっているとした上で8等分した角度なので θ/8、(θ+360)/8、(θ+360×2)/8・・・(θ+360×7)/8のcosを取っていると解釈できる。 n半角の公式では1つの角度に対して一般にn個のn半角があるので、cosやsinも一般にnつある。 ある角度のn分の1が一般に複数出てくるのは、複素数のn乗根が一般にn個出てくるのと同じことである。 クリえもん<のび太くん、縮退は解けた解?  にほんブログ村  「昨日、何計算してたー?」 「昨日、何計算してたー?」 「あー、俺はジローラモ演算で遊んでたよ~。そっちは?」 「あー、俺はジローラモ演算で遊んでたよ~。そっちは?」 「こっちはド・モッタガンの公式とニコ定理と4次方程式を練りこんで8半角の定理を作って食べたよ~」 「こっちはド・モッタガンの公式とニコ定理と4次方程式を練りこんで8半角の定理を作って食べたよ~」 「うまそやねぇー。ところで明日さ、暇だったら 「うまそやねぇー。ところで明日さ、暇だったら 「お、いいねいいね、じゃあ明日12時にマスバーガーで~」 「お、いいねいいね、じゃあ明日12時にマスバーガーで~」疲れているとホントにすっかり忘れるもんですね。 ノートを見て思い出しました。 あー・・・こんなに熱中してた計算をどうして今忘れているんだろうと思いましたよ 九九の表ってありますよね あれを10の段まで増やすとこうなるんですが 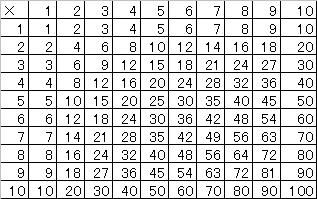 この1~100までの数を11で割ってあまりを求めて、それをこの表に上書きするとこんな感じになります。 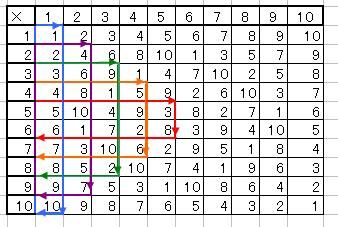 カラーの矢印で囲った部分は、矢印どおりに読んでいくと矢印で囲った部分だけに表が省略できますよーって意味です。 たとえば、この表の上から5行目、左から6列目の4×5=20に注目しますと 11で割ったあまりは9になりますよね 左から4、8、1、5・・・ってたどって行くんですけど 5の1つ右も、1つ下も9じゃないですか。 下にたどればいいので、右半分はいらなくなるわけです。 また、下に3マス進むと4×8=32を11で割ったあまりは10なんですが 4、8、1、5、9、2、6ってたどっていくと その1つ下も1つ左もちゃんと10になってますよね ということでこっから下もいらないんです。 では再び、4×5=20に話を戻すと 20を11で割ったあまりは9なんですが もし仮に○×5=9になる○のほうが欠けていた場合どうしましょう? 今の場合は4を出したいわけです。 掛け算で言うところの、4×5=20の○×5=20になる○を計算したいわけです。 これは割り算ですよね 20/5=4 でもあまりの計算のときはちょっと面倒なので そこでこんな表を作ってみました。 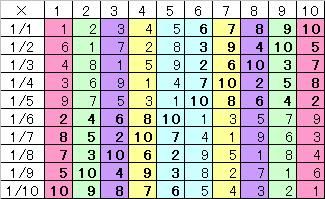 20を11で割ると9なので、まずは左から10列目の9の段を参照します それから、5で割りたいので、6行目の1/5の行を参照すると ちゃんと4が出ました^^ 実は、この同じ色の縦のラインは右が左の上下逆さまなので 下半分が丸々不要ということになり 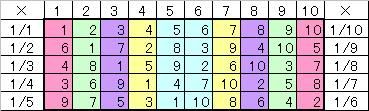 このような表に略すことができます。 オモシローイネー  にほんブログ村
容量2倍リチウムイオン電池 阪大・市大共同開発
顔文字→式でいくぜ!.ExE ψ(・∇・)ψ ↑位置と運動量の不確定性原理界隈にこんな顔した式、いるよな!?  工位先生って匠なん?でもToTってジト目だよね 涙目  にほんブログ村
ココ「ねえ、滝丸。僕たちキャラかぶってるよね?なんで一緒にいるんだろう?」
滝丸「作者がカブってるネタやろうとしてるからじゃないでしょうか」 鉄平「じゃあウチの曽々々々じいさん呼んでこようか?あれ?曽々々じいさんだったっけ?」  スキージャンプ・ペアやハイジャンプ・ペアに並びつつあるゴリンピック競技、グルメバトラーのキャラがかぶっている人たちのことを「トリコなおにいさん・ペア」と呼ぶ。 「ハァイ、毒夫とロン毛の髪の長いほう、滝丸です。」 「ハァイ、毒夫とロン毛の視力がいいほう、ココです。」 「「2人合わせて、バンダナーズ・イケマンズでぇーす」」 「「ほら、やっぱりカブってる」」  にほんブログ村
僕は結婚してもいいです(・ω・)大山さんと。
 ダイガードじゃなくてダイガードが日9だったらな!・・・あれ?長年の癖でIの直後にHが押せない・・・! どうしてもGを押してしまう!隣なのに!隣だからか! 地球防衛企業ダイ・ガード  にほんブログ村
サドルにブロッコリー 東大駐輪場の自転車20台に
犯人A1「ブロッコリーにしようか、カリフラワーにしようか・・・そこが問題だ」 犯人A2「じゃあもういっそのことロマネスコにしとけよ、複素数でフラクタルでフィボナッチなんだからフ尽くしだぞ」 犯人A3「ヤンヤンヤン大王の怒り~今日、フのダイコン味噌汁が降り注ぐ~ヤンヤンヤンやわらかヤンクミ~」 犯人A1「そういやカリフラワーってブロッコリーより高いの?」 犯人A2「知らねえ。ってかロマネスコってどこに売ってんのよ」 犯人A1「まあいいや、俺の目的はささやかなイタズラとささやかなプレゼントだしな~メリー体育の日~、みたいな。ちょっとブロッコリー買って自転車に挿してくるわ~」 犯人A1「サドルは自転車の脇にそっと添えて・・・と。俺ってば小粋ないい人~^^」 以上、脳内会議。 1時間後 犯人A1「あれ!?置いといたサドルたちは!?」 犯人A1「なあおい、ここにサドルあったよな!?」 通りすがり「あ、そういやなんか、さっき回収してたやついたよね?」 犯人A1「ええ~!?(ヤバい・・・これじゃ俺、名乗り出られない・・・!!) でもなんの目的で・・・!?」 通りすがり「そりゃ転売目的っしょ。それか、警察が不法投棄認識して回収したんじゃないっすか?ってかそもそも、ブロッコリー挿すほうが目的わかんないですって(笑)」 犯人A1「(どうしよう・・・これじゃ俺、名乗り出られない・・・ってこれさっきも考えたよね!?) おのれ警察め!軽率なことしやがって~~~~!!!訴えてやる!(訴え返されるか・・・orz)」 通りすがり「いやそんな、憶測を鵜呑みにされましても・・・」 海賊戦隊ピースメイン  にほんブログ村
1.つながってる線で、交差点全部に入り口と出口があれば、一筆書き可能。
2.1の例外として、奇数本出てる交差点は1対まで認める。 このときの書き方は、入り口から出口に向かえばおk JIN:入り口と出口は同じじゃないねん  にほんブログ村
軌道エレベータ(宇宙エレベーター、軌道タワー、宇宙タワー?)ができたとして、そのタワーを使ってどうやって物資を運ぶ方法を早くも競い始めてるみたいなんだけど
エレベータじゃなくてエスカレータにすれば楽じゃね? 厳密には「軌道エスカレーターのち軌道歩く歩道」なんだけど 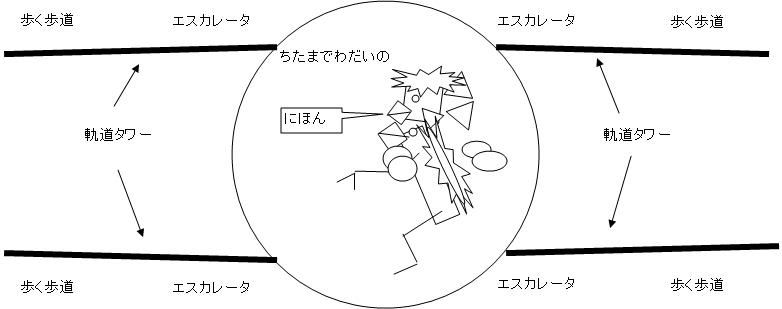 タワーを赤道に建てようとするから真上に持ち上げなきゃならないわけで 中緯度に建てれば遠心力と重力の兼ね合いで、斜めにそびえ立ってくれる そこで物資の重さをもっとタワーに頼れば、運ぶの楽にならないだろうか まあ、中緯度に立てる話は前からあったけど 現実視されてなかったんだよな でもやっぱ、でっかいタワーが真上よりも斜めにそびえ立ってくれたほうが面白そうじゃん 最初はエスカレータとして乗って 重力が減って遠心力が増すにつれて階段が歩く歩道になって行きながら しだいに無重力を体感していくわけ。 なんか楽しそう! あ、そういや、もっと上空に行ったらほぼ遠心力だけになるから むしろ「下りエレベータ」になっちゃったりしないかなぁ まあ、地球外との中継地点がタワー全体のほとんど下部分になるはずだから 下りエレベータを体験するのは娯楽以外の何物でもないんだろうけどね やねよーりーたーかーい こいのーぼーりー  にほんブログ村
どうして円高なのに1ドル100円から50円とかに数字が減るのか
わかりやすく、相対性理論のE=mc^2でイメージしてみよう Eはエネルギー、mは質量。 cというのは光速で、秒速30万キロっていう速きのことなんだけど これを2乗したものを質量にかけるとエネルギーになるということは 1gの1円玉がそのまま全部エネルギーになるとすると約100テラジュールのエネルギーが得られるよーという意味がE=mc^2に込められている。 キロワット時に直すと、20億kWhをゆうに超える 1円玉で発電所レベル。 しかしながら、この相場は現在ひっじょーに成り立っておらず 非常にエネルギーが高くて質量が安い状況が続いている むしろ成り立っていたら色々とドカーンだドカーン! 3500kcalも消費してそれでもなお体重が500gしか減らないレベルなのだから さきほどの1g1テラジュールと比べると 1gたったの10キロジュールとなって、エネルギーの価値が質量より10桁も高く、エネルギー高質量安であることがイメージできただろう・・・か。 このように、やはりエネルギーの単位であるジュールのほうが小さいのにエネルギー高となるのは、系の理文を問わず本質的に単位の問題だということがわかった。 そういえば昔、 「欧米では日本のように1[円]などと表記せずに 1/円と表記したりする」 という話を聞いたことがある。 この「/」はまさに割り算の意味の分数記号である。 真偽のほどは定かではないが、理にかなってはいる。 どういうことかというと 値段=円=3という式があって 値段が文字、3が数値、円が単位で 値段=3[円] と、3と円の間のイコールを抜かしてこう表記するのが日本式 両辺を3で割って右辺を常に1にするように (1/値段)円=(1/3)円=1 と表記するのが欧米式 ということのようだ。 つまり、単位と数値は一見並べて書かれているようで、実は打ち消しあって単位を無にするような間柄でもあったということなのだ。 1ドル50円の例で見てみると 日本式:1(=)[ドル]:50(=)[円]なんだが 欧米式:1/ドル=1=50/円 でもあり、両辺の分母分子を入れ替えると (1/1)ドル=1=(1/50)円→0.02円 1ドル100円と比べると 1[ドル]=100[円]でもあり (1/1)ドル=1=(1/100)円→0.01円 という意味だったのだ。こう考えると、 「なるほど、そりゃぁ確かに1ドル50円のが円高だわ」 という素直に納得する気にもなろう そういえば、簿記の締め切り方にも大陸式と欧米式※があったな 大陸ってのはどの大陸のことなのよ?ってのが結局わからずじまいだったっけ パンゲアかムーか、アトランティスか ※欧米じゃなかった。英米かっ! 1000円玉と50円玉と20円玉です  にほんブログ村
「量子メモリー」の原理を実証
量子コンピュータくんは、  こんな感じの、最大公約数回答ゲームがあったとしてですよ こういう初級は   苦手なんです。 中級にいくと   こんな問題も用意されていて  こっちは多少できるんですが  初級で躓いてしまうので、解きたくても解けない>< そこで そんな、難題ほど燃えるタイプの量子コンピュータくんのために 最初の画面に「上級へワープ」ボタンが用意されていたりして   なんかレトロなセーブ機能になっていてですね 上級の問題は   こんな感じなのですが、すぐに解けちゃうわけです。 まあこういった問題がいくつか続きまして 上級だと  速攻で全問正解してこうなるっていうのが量子コンピュータくんの性能なわけですよ。 ただ、他のゲームになるとまたコンピュータを組み直さなきゃならないんですよねー>< 量子コンピュータくんは、このゲームを解くためだけに作られるハードウェアさんなわけ。 ここをどうするかが問題。 どっちかっていうと量子コンピュータはアナログコンピュータですから。 汎用性がないの。 アナログ  ルネッサーンスこいよ! ルネッサーンスこいよ!って感じです こういう日記はモチベーションが下がると、 暖めなおすのに結構くすぶりましてね アニメ「日常」が終わって「こんなのー」ができなくなりそうな雰囲気だったのですが このニュースに意欲をもらって、感謝感謝でございますよ^^ まさにはかせ!はかせ並みにシュール!  にほんブログ村
二項定理というものを習った覚えがあるだろうか
たとえばx+1の2乗や3乗などを計算するのに便利な定理なんだが、 組合わせ記号mCnを使って (x+1)^nを Σ(nCi×x^i) (0≦i≦n) と展開できる。 しかしながら、この定理自体や組合わせ記号の定義 mCn=m!/n!/(m-n)! などを忘れてしまっては意味がない そこで、二項定理を11の何乗で覚やすくできないかと考えた。 つまりこういうことだ 係数のmCnを11のべき乗の筆算を使って導出するのだ。 たとえば(x+1)^2=x^2+2x+1の1,2,1という係数を11の2乗によって以下のように導出する。
ただし、係数が10を越えて2桁以上になる場合には注意が必要である。 たとえば、(x+1)^6=x^6+6x^5+15x^4+20x^3+15x^2+6x+1の係数1,6,15,20,15,6,1の係数の場合 20や15が2桁になる これは11を6乗する際に11^6=(11^2)^2*11^2を筆算してやって、その係数を求めるわけだが この筆算の足し算のさいに隣の桁に繰り上がりの影響を与えてはいけない。
また、11のべき乗から逆に組み合わせmCnや順列mPnを導出するのもアリかもしれない 11の4乗あたりまでやって、14641の数列を見て、右からn番目を4Cnとしてみて 確か4C2=4C4=4だし、4C1=4C5=1だし、4C3=6で左右対称だから なんとなーくうすぼんやり4C2=4・3/(2・1)=4・3・2/(3・2・1)=4C3(3つと2つ)とかってやったなぁ って思い出せれば 分子にはたぶん4の階乗があって、3つや2つの積にするために2や3の階乗で割るんだろうと考え、 その上さらに左右対称なんだから4-nの階乗とかで割ってるんだろうなぁってとこまで考えると mCn=m!/n!/(m-n)!ってことが試験中でも芋づる式に思い出せる。 で、この分母のどっちかがなくて、nが大きいときにびっくりするほど大きな数になるのが順列のmPnだってことさえ覚えていれば たとえば1~5までの数から4つ抜き出す「順列」を連想したりしてみると、n!と(m-n)!のどっちを抜かせばいいかってことはおのずと導き出せるはずだ。 まあそんなわけで、(cosθ+isinθ)^8=cos(8θ)+isin(8θ)を証明して、 8半角の定理でも導いてみなさいよ^^  にほんブログ村 魔法少女といったらピクシーミサ
そういう間柄でありたい、みたいな。 吼新星 甲信越乱れやまびこ そういえば更新世乱れやまびこを久々に見た気がする あれってダイレンジャーだったのか。 1993年かぁ。超新星しか覚えてなかった。あと、甲信越るのがシルバーっぽかったのと。 それと、いまだに 石松はハワードザダックのフィルに見えるし、きっとサマタイの主人公が「ありがちキャラ」なんだろうな。 上から読んでも下から読んでもいかりかい サマータイムマシン・ブルース 伊狩鎧がある  にほんブログ村
ニュース - 科学&宇宙 - なぜ宇宙は加速的に膨張しているのか
相対論的エネルギーがマイナスなんでしょ? だったら こう じゃなくて こう じゃね? はい大事なのはX軸の位置ねー っていうかどっちでもいいのかなぁ? ちょっと待ってよ そういえばマイナスの積み上げ棒グラフってなんか変だよなって前から思ってたんだった たとえば毎月の出費を分類して計上する際、交通費の勘定科目について 会社から支給されたのが実際のガソリン代よりも多くなっちゃった!てへぺろ(・ω<) みたいなことがあったらどうやってグラフに反映されるんだろうっていうのがいまいちよくわかってなかったんだよ どうも、あくまで別枠で改めてマイナス部分に積み重ねられるみたいね ほらこんなときも こんなときも 交通費だけじゃなく、趣味の費用でも出費がマイナスだったりしたら(薄緑) あくまでプラスの雑費上(紫の上から折り返す感じ)から上塗りされるんじゃなくて ゼロから下の交通費(ベージュ)のさらに下に足されるんだよ。 ある意味合理的だよな。だって、全体としてはあくまで100%維持してるんだもん でもそれでよかったのかなぁ? いまいち釈然としない。 だって、交通費がマイナスになったぶん出費が減るんだから、棒グラフとしては短くなるべきじゃん あ、でもそういえばこのグラフを出費だけのグラフではなく 出費と同時に収入もマイナスの出費として扱うグラフに拡張して解釈するとどうなるんだろう? その場合、もはや棒の長さは意味を成さなくなるのか? たとえば先月より今月の出費が200円少なくて、収入が300円多かったとき 上には短く、下には長い棒になる。この全体の長さという量に意味は・・・ないかもな。 だって、収入的にも出費的にも利益は増してるはずなのに、グラフとしては200と300が帳消しになって100円分しか長くならないからなぁ。 あくまでゼロ(X軸)の上と下で分けて見なきゃダメってことか。 あーなんか急にちっちゃい話になったな。 とかいって10のマイナス34乗までちっちゃくなったとかいったらそれはそれでデカいんだからな!? スケールってのはあくまでべき乗の絶対値で考えるべきなんだよ。べき乗だけに。 でっかい話に戻そう 今回のノーベル賞受賞者ってダークエネルギーの3人だったんだ!? いつも思うけど、ノーベル賞発表の時期ってどうも覚えられねえ 毎年なのかどうかもよくわかんねえ 前まではなんだ ニュースになったから受動的に見れてたんだけど 最近テレビ見なくなってから ネットで取捨選択するニュースって取捨選択なんだわ、能動的だから。 だから見落とすんだよなぁ こりゃ見落とすなぁ フツーに、「あ、この芸人消えたよね?」って思ったのが、実は消えたのは孤独な観測者のほうだったりして。 我思わん、故に何も無し みたいな。 我、相生だけに愛を稲荷寿司で包むナリ。なんつってな!オバQみたい! あ、ホントだ!はかせ足元が最初からオバQだ! おまけ  にほんブログ村 |
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





