|
20080511～
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
主に、クォータニオンに取り消し線がつけられて寂しい
いまどき3Dの気象シミュレーションにはクォータニオンを使うのかなぁー とか思ったけど、そうでもないのかもしれない まあ、有限要素法とか差分法にクォータニオンっていう組み合わせがいまいちイメージしづらい感じはする。うん や、昔ね、趣味で気象予報士の知識を得ようと思った時があって 相変わらず飽き性だったから地衡風だけそこそこ勉強して飽きちゃったんだけど そんときに「ベクトルめんどくせー！」って思って、勝手にフェーザーに改造したことがあって あとから、その方法論の名前を聞いたはいいけど すっかり忘れてしまって。 結局そんときは、「『オリジナルの予報則を作ってみよう』ってなんやねん」で終わってしまったけど そのときですね 「中学の知識って意外と使える」って思ったのは。 高校生のときに地学とか生物とかの選択肢がなかったので、取りようがなくて 気象に関する知識もいまだに中学レベルなんですが 温暖前線・寒冷前線・閉塞前線・停滞前線とかを一通り知っていると ある程度通用するようにできてるんですよね。 お天気お姉さんとかお天気おじさんとかの言ってることがだいたいわかりますよね 電気や数学・情報などの理論についても ああ、ちゃんと中学高校から地続きなんだって改めて思います。 でもその地続き感が、習ってる当初としてはあまり居心地がよくなかったりして。 特に形から入るタイプの人だと、地味～って感じがしちゃうんでしょうね 気象に関しては、僕の知識レベルは 台風が反れるのってそれコリオリじゃねえの？ レベルです。 台風の中身の風はコリオリに影響されますが 台風自体はなんで反れるのか、いまいち理解してないんですよね なんでしたっけ、気団(高気圧)に押されるとか、貿易風だか偏西風だかの蛇行に巻き込まれるとか こまごましたところだとそういう理屈らしいんですが じゃあ結局コリオリ関係あんの？ないの？って感じなんです。 南半球でも結局東にそれるし。 でも北半球に比べてサンプルが少なすぎるんですよね 陸地がねーの。 っていうか台風の速度と質量とサイズの規模でコリオリ力をまず計算すればいいじゃん。それな まずそれやろうな？俺
昨日、多項定理を思い出したばかりでなんですが
よく考えたらマクロなしExcelでもできるや。 たとえば (-w+x+y)(-x+2y)とかいうやつ。 動的メモリ管理が怖いのであれば、ひとつの多項式には項が高々4つか5つくらいしかないととらえて、最大10とか100とかにすればいいし 2yについては(-x+y+y)にすれば単純なモデルとして考えることができそう。 それから、掛け算したあとの項を アルファベット順と定めておいて、文字の切り離しと連結を行う 最後に、パターン検出をして、数を確認すれば終わり とすれば、さほど難しいことでもないかもしれない まあ最初はバグ取りのために手動で動作確認するよね。ｃｔｒｌ＋ｆとか使って人力で数えるとか wxyとwx、xyの区別もしなきゃならないし。まあそこは「完全一致」を条件にすればいいか。 ちょっと面倒なのが(-x+2y)とかのマイナスだよね。 なんかこう、全部足し算にする方法とかないだろうか。2の補数的な。 それにしても疲れたな。 今朝にかけてきんモザ一挙を2期分見てたからってのもあるけど 最近はちょっと数式とプチケンカしたような感じになってる
35歳の脳にはって意味もありますが、バイト複数掛け持ちしながらだとキツいっていうのもありますし
授業を2つ受けながらって意味もあります。 もう1つは数学で、習ってること自体は結構簡単といいますか 特殊ユニタリの演算を趣味でやってる側からすると高校の数学のようなといいますか でも、この授業で雰囲気に当てられて、特殊ユニタリについての理解が自力で深まっているのは事実のような気はします。 アレです、節約してる人が友人に連れられてドーナツ屋に渋々行かされると意外と高価な買い物(最低限の値段でないもの)をするっていうのに似てます。 しかし、年齢や経験のせいもありますが なかなか頭が硬くなって、計算に集中できず、飽きてしまうまでの時間が短くなったように感じます。 そんなとき、マセマティカのような、解析計算向きのソフトがあればいいのにと思いますが 高いんですよね。(もう安いのかな？) もし、マセマティカの簡易版の簡易版のｒｙのようなものが作れたらいいのに と思うことはあります。 たとえば「多項式同士の積の同類項を整理してくれるツール」があるだけでもだいぶ助かると思います。 でもそれを作るには、プログラミングで文字列を扱わなければなりません。 情報工学の人なら楽勝かとも思いますが 電気工学出身の僕にはどうもその辺の知識と練習量が壊滅的に抜けているようなんです。 ポインタでつまずく、オブジェクト指向でつまずく とよく言われましたが、オブジェクト指向につまずく人は減ったかもしれません。 というのも、どうも先生に聞いてみたところ 15年前のｃゲンガーが思うアセンブラのじゃじゃ馬っぷりは 現代のオブジェクターの思うｃゲンガーのじゃじゃ馬っぷりに似ているというのです。 なんとなく雰囲気だけはわかりかねません。 しかし、相変わらずポインタでつまずいている人が多いような気がしないでもない そして、そのポインタと文字列操作にはどうも密接なつながりがあるようなんです。 今の僕には、そこのとっかかりがいまいちつかめていません。 もし、時間と体力の余裕があれば、まだなんとかなったかもしれませんが どうもとりあえず無理かもしれません。今のところは。 もしも来期生まれ変われたら、1科目だけ取りたいです 経費削減ワンチャンあると思った？ この4月からの授業で、アロー演算子というものの存在を初めて知った気がします。 構造体もろくに習わなかった気もします。 しかし、学生当時はそれでも「専門はプログラミング(寄りの電気)」といえたのです。 当時の技術のせいなのかどうかわかりませんが おそらく電気工学の人がプログラミングで扱うものは大概数値だけ っていうスタンスだと、確かにポインタをまじめに習うようなカリキュラムは必要なかったかもしれません。 有限要素法や差分法で配列を組む際に本当に不必要なのかはわかりませんけどね。 めっちゃ遅いプログラムを結果的に組んだかもしれませんし。 いまだに、どうして文字列が対象だと変数がポインタになりがちなのかわかりませんし scanfの変数のところにアンパサンドをつけるのかもよくわかってません。 「呪文」以上の納得する意味を見つけられていないんです おそらく、これは電気工学における僕の体験 「電気回路の電圧・電流と水圧・水流の関係」ぐらいに基礎的なことで、わかってしまえばあとは楽ちん なところのような気もします。 変なところでこだわる癖があって、でもそのこだわりのおかげで回り道しながらも理解が人並みより少し深い ような気がします。これはアスペの強みといえるでしょうか？？ そういえば「平方センチメートルとセンチ平方メートルの違い」のようなもので漠然とモンモンしていた記憶がありますね なぜ漠然なのか。誰も疑問に思わないから、自分で解決するしかなかったからだと思います 今だったら大概、知恵袋に載ってますよね 「マイナス1を7で割ったあまりははたして1か」 についても漠然とした問題提起が大学まで続いて すでに解消されていることをそこで知りました。 「二の段で結果が奇数になる掛け算の逆元」についても漠然と考えていたような気がします 「3で割ったあまり」と「9で割ったあまり」の部分集合？群？についてもでしょうか
最近、宇宙パトロールルル子がよくわからない。
まあ元来、よくわからないことを売りにしているアニメ制作会社のようなので そこそこ万人受けが成立してるらしいんだけど トリガー作品愛好家ってほどでもない僕は キルラキルしか話がわからなかった。 というか、キルラキルしか話がわからなかったことがわかってよかった。 何週か前に「知らない作品のパロディをやったらどうなるんだろう？」という疑問をルル子が解決してくれるかもしれないという期待をしていた気がする 現実で夢を見せられている状態とはよく言ったものだ たぶん、これはかねてから僕が抱いていた疑問の答えに近い。 「タイムトラベルもの」がまだ流行らなかった過去に、タイムトラベル作品の集大成と称されるシュタゲを見せたらどんな感想が得られるか という疑問だ。 称賛されるか、一周回って嘲笑されるか、どちらでもないか。 もちろん、古代人であればどのような大衆でもいいわけではなく、タイムトラベルものに関して興味はあって考えてはいるけど、そんなに情報があふれていない時代 ということで僕がシュタゲのビデオとテレビデオを持っていきたい時代は古代ギリシャだ。 そんな願いが実現するかしないか、仮に実現するとしてもずっと先の話だろうというのは想像がつくので、 自分を実験体にできてよかった。 その上、作品サンプルの提供もトリガーさんで本当によかった。 決して悪い印象ではないが、よくわからない！！ﾎﾟｶｰﾝﾟдﾟ； なるほどそうか、こういう感情になるのか。
あのあともう少し考えてみてたんですが、
実数解もちゃんと3つ、cosつまり-1から1までの間にありましてね cos(x/3)=cos{(x+2πn)/3} sin(x/3)=sin{(x+2πn)/3} だったことがわかりました ∧∧ ヽ(･ω･)/ ｼﾞﾒｰ ＼(.＼ ノ ､ﾊ,,､ ￣ ￣ しかしよく見るとこの式、やっぱりまだちょっとおかしいですね。 qにつく符号が一部、逆になったままです。
struct お茶漬け{
飲料 お茶； 主食 レンジでチンご飯； 雑種 お茶漬けのもと； 日付 祝日； 曜日 土曜、日曜； }； なお、犯罪の対象となるのは犯行宣言のみであり、犯行そのものは犯罪ではない模様。
3倍角の公式を、オイラー・ドモルガンの関係から導きます。
二項定理で展開し、実部と虚部を比較すると、3倍角の公式が出来上がります。 じゃあ3分角の公式は？ 3x=Xとすると、3倍角の公式は3分角の公式になりますよね cosxについての3次方程式を解いてみましょうか。 cosx=c、cos3xをc3とでもおきましょうか。 カルダノの方法を用いて、cが実数になる範囲で解いてみましょう。 途中で変数を定義しますと、このようになります。累乗根を求めやすいように、極座標にしちゃいましょう。 3乗根を取ると、このようになります。 複素3乗根なので多価なんですが、ここでは1つだけ代表します。 v1とv2の組み合わせとして、3v1v2=pになるような条件があるのですが、ちゃんと成り立っていますね。 求めたいcは、v1とv2の和です。複素数なら一般に3つあるのですが、実数の範囲内ではこれだけです。 それでは、pとqを代入してみましょう。 こうして世にも自明な恒等式が導かれたのであった・・・orz
以前、ちょうつがいの式と題して、
MMDの多段ボーンの理論のようなことを書いたことがあったのです。 これとかこれとか 一旦重心を原点に移動して、原点周りの回転をさせてから、元の位置に戻す。 それよりもっと前に、二次元での任意軸回転で困っていたことがあって 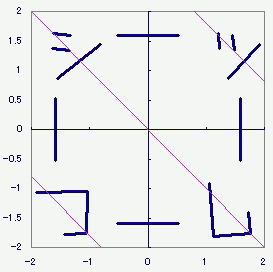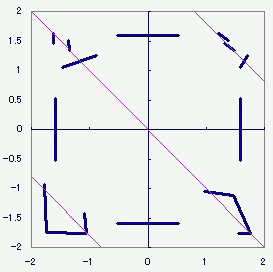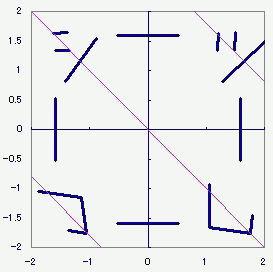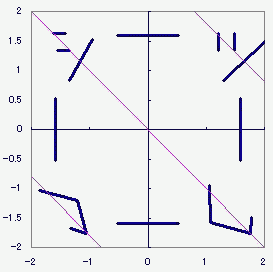 反逆関数ようやく気づいたんですが、傾いた直線を軸に回転させたければ １．その傾いた直線ごと、図形をまるっと一旦x軸かy軸まで持っていって ２．それから回転なり反転なりさせて、 ３．それから図形ごと傾きも元に戻せば よかったんじゃないすか 気が付かなかったなぁ
解が実数になる範囲で解いたら
cos(θ/3)=cos(θ/3) って自明な恒等式がただ得られただけだった・・・還元不能ってこういうことを言うんですかね？
デキューちゃうわ！
昔のMSペイントには、画像変換ツールとしてまともなのがほとんどなく、スキューくらいしかなかった ぶっちゃけ何の用途で使うのかいまだによくわからない。 特殊相対論で斜交座標系に使うにしても、伸縮も考慮しないスキューだけでは意味がなかろう 回転すらなかったのである。 まあ今でもないけどね。 あるとすれば回転というより反転と呼べるものだけ。 そういえば、ベクトル演算プログラミングと聞いて、何がよくなったのかわからなかったが 友達に説明を聞いて、 「ああ、MSペイント方式とエクセルのオートシェイプの違いみたいなもんか」 と納得した。 Excelのオートシェイプに手を出すのにずいぶん長いこと躊躇してしまった理由の１つに ドット処理しないPC内部空間への不器用性の表れ というのがあって たとえば僕はテープをまっすぐしわなく貼れない人間なのである。 その上、まっすぐ貼ってるのか斜めになっているのか、僕の判別は極めて雑らしい これまで、アボガドロ規模の正確さについて完全に無気力だったので、そういう力が乏しいのもある意味当たり前である。 ただ、デジタルであればPCの中だろうが外だろうが完璧主義である。 ドットで書くならどんなまっすぐな線でも書いてくれよう。 また、木に穴をあけるタイプではなく、元から穴が空いている金属へのネジ締は任せてくれ ただし、強度についてはトルクレンチがないと何とも言えない ただ、自分ができずに悔しがっている分野へのあこがれは常に強くある傾向があって ロボットのパイロットである主人公が事務処理をやっているアニメ 「ダイガード」には憧れたし 社会科全般苦手なので、政治的な話が絡むロボットアニメは結構好きだったりするらしい(両極端になる傾向もある) ロボット出動にハンコならガオガイガーでもあるが、捨て印と割り印が出てきたダイガードには正直しびれた。 また、アナログコンピュータや計算尺、デジタルだけど機械式のコンピュータにもよくわからないロマンを感じる 最近だと、絶対業務で使いたくはないが、興味だけはあるのが、和文タイプライター せめてハンコを押す位置ぐらいはグリッド単位にしてさしあげろと思う ハンコの位置をカスタマイズできないのは、まあ仕方ない。自由と不自由は同じだわ
意外と話題になっていないようですね。
Excelでカットアンドペーストすると、コピペーとは違って、絶対参照しなくてもズレないのは ポインタをカッペーしているおかげ ただし、リファレンスエラーになることがあるので注意 っていう話なんですが プログラミング恐怖症になって長いので、しばらく避けていたら ポインタの概念を忘れてしまって 今習いなおして思い出して、 あ！これだ！ポインタって言葉を使いたかったんだ！ ってなったんですよね。 で、さっそく「Excel ポインタ」とかでぐぐると、 マウスでポイントするほうのポインタが出てきてしまいますorz ソレチガウ どっちかっていうとジョン・ヘンリー・ポインティングさんのほうや。 レーザーポインタはすごく愚直にポインティングベクトルを可視化しているいいデバイス例だと思います 電池と抵抗からなるもっともシンプルな電気回路をかかげて ポインティングベクトルは今どっちを向いているでしょう？と考えさせる授業はいかがでしょうか 電球につなげてしまうとややこしいのでNG あ、いや、でも抵抗でも赤外線としてジュール熱があばばばば 話は戻りますが、やっぱりポインタでつまずきなおしています。 というか、これが一度目かもしれません ああ、そういえばカッペーとコピペーでシュタゲの岡部を思い出しましたが 意識や自我や魂というのがポインタである説はもう出ましたでしょうか？？
gifやapngのことである。みみっちい！ うーんこの量子能 アスキーアートアニメーションのgifとmidiを並列したものを待ち行列にして 直列に並べた動画配信でアニメのOPを見たい。 たとえばごちうさOPの「歌声も込みでフーリエ変換してmidiにしちゃった人」リスペクトとかで 演奏してみろタグｲｲﾈ・ もちろん、各タイミングは外部ツールで切り張りするんだよ！勝手に窓が開く。※窓です 息を止めた午前5時※午後です ※謹賀新年＠ばくごおんOP BecK-on to the FUTURE
仮説の段階なのでまだなんとも言えないのですが いやだからこそこういうことを仕方なくやっているのですが もしこのモデルが正しいのであれば、半径は固定なのだから、 15個ある4次の特殊ユニタリ生成子をランダムに出してやってる間に 4つの固有値のうち、もっとも絶対値が大きくなるものを試行錯誤して暫定で出してやり、 それを半径とした上で、角度の関係を数値的に予想する という手法はとれると思います 問題があるとすれば、、角度がゼロになりえないように2つの係数とエルミート行列が結託して企んでいるとしたら エセ半径しか算出できませんけどね・・・ やっぱ天気が悪いと調子もガクッと落ちますなあ まあ、ここんとこ多忙だったせいもあるんですが。
|
カレンダー
カテゴリー
ブログランキング
ブログランキング参戦中
よかったらポチッとお願いします＾＾
最新CM
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
[03/17 Robertaverm]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
ＨＮ：
量子きのこ
年齢：
44
ＨＰ：
性別：
男性
誕生日：
1981/04/04
職業：
WinDOS.N臣T
趣味：
妄想・計算・測定・アニメ
自己紹介：
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例：H→7番目、XP→15(P)×26＋23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいｽﾞｺｰ
バーコード
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|
