2の偶数・奇数乗と3の倍数±1

2の偶数乗-1≡0(MOD3)
2の奇数乗+1≡0(MOD3)



追記：なんか拡張できた。
①n（≡2＠MOD3)の偶数乗≡1＠MOD3 
②n（≡2＠MOD3)の奇数乗≡-1＠MOD3
③m（≡1＠MOD3)の整数乗≡1＠MOD3


もちょっと追記：
例
①
2の8乗=256≡1＠MOD3　(256÷3=86あまり-2)
5の4乗=625≡1＠MOD3　(625÷3=208あまり1)
(-7)の2乗=49≡1＠MOD3　(49÷3=17あまり-2)

②
5の3乗=125≡2＠MOD3　(125÷3=41あまり2)
2の5乗=32≡2MOD3　(32÷3=11あまり-1)
(-4)の3乗=-64≡2＠MOD3　(-64÷3=-21あまり-1)

③
4の3乗=64≡1＠MOD3　(64÷3=21あまり1)
7の2乗=49≡1＠MOD3　(49÷3=16あまり1)
(-2)の2乗=4≡1＠MOD3　(4÷3=1あまり1)
(-2)の3乗=-8≡1＠MOD3　(-8÷3=-3あまり1)





10進数の数の2乗を繰り返すと下1桁(10で割ったあまり)は0か1か5か6に収束する。
そのうち、5で割り切れる下1桁は最初から最後まで収束している。
残りの、5で割って1余る下1桁は他の数から収束する。
●2の2乗=●4→●4の2乗=●6→●6の2乗=●6(シュタゲ)
●8の2乗=●4→●4の2乗=●6→●6の2乗=●6(シュタゲ) 
●3の2乗=●9→●9の2乗=●1→●1の2乗=●1(シュタゲ) 
●7の2乗=●9→●9の2乗=●1→●1の2乗=●1(シュタゲ) 
●0の2乗=●0(電王)
●5の2乗=●5(電王) 




帰納法と背理法が時々ごっちゃになるねん

にほんブログ村

今日の、定理。～ドラビアン内藤～

自然数nの奇数乗+1という多項式はn+1という多項式で割り切れる。


n^(2m+1)=0　(mod　n+1)

エクセル風に書くと
mod(n^(2m+1),n+1)=0


たとえば1001＜アラビアンナイト＞を11で割り切る話夢の続きは
2つマルをつけて100001/11=9091あまり0だとか。



久々に多項式の割り算を行った。

オマケ
こんなのも言えそう。


↓間違えたこうだや＞＜↓


これがあればx^3+1の因数分解をするときに符号で迷わなくてすむかも！
10万と1夜を思い出してね！イフリータ！



ヒモとヒモの間に0は偶数個。

にほんブログ村

今日の、定理。(計量テンソル)

テンソルっつってもたかだか行列じゃんか。よかったなお前ら3次元人で。具体的に平面に書けるぞ！

計量テンソルを三角行列に定義すべきか、山分けして対称行列に定義すべきか
って思ったけど、三角行列の固有値は対称行列以上に簡単！
エルミートとか言ってないでまず三角行列でおｋ←結論。


というわけで今日の定理。
三角行列の固有値λはすべて対角成分である。(三角行列の行列式は対角成分の積である(三角行列のトレースは対角成分の和である：何当たり前のこといってだ！))
あ

計量テンソルを例にやってみる。


ほんまや！なんてこった！歪み要素出番ナシ！



ちなみに固有時(時空間隔)ds^2はこんな風にブラケット表記することが可能！
ds^2=<x|gmn|x>

4列の行ベクトル「ブラ」は<x|=(ct,x,y,z)で、「ケット」|x>はその（共役複素？）転置である4行の列ベクトル。
平らなミンコフスキー時空だと-g00=g11=g22=g33=1で、それ以外が全部ゼロなので(|gmn|=δmn：クロネッカーのデルタ)
ds^2=-(cdt)^2+dx^2+dy^2+dz^2になるよ！
g00だけにマイナスがついているからﾐﾝｺﾞｽﾌｷｰ時空が楕円ではなく双曲線なんだね！4番目の次元は異常。

双曲線関数がどうして双曲線関数と呼ばれているかは、三角関数で楕円を描いた要領で
双曲線(x/a)^2-(y/b)^2=±1のxとyをθで媒介変数表示してx=±acoshθ、y=±bsinhθにすればいいよ！(複合同順じゃねーよ！)
これをa=b=1にして45度傾けたら反比例の式xy=±1になるから数学ってのはどこからやぶヘビが出てくるかわかんないね！





おっぱいはホントよう歪むですよ！ブラcats！

にほんブログ村

n個の点を結ぶ線の数は(n-1)?(ハテナ)本

ただし、ハテナ記号は僕が今勝手に作った階和とか階加とかいう記号で、
整数nのn?はnから0あるいは1まで1つずつ減らしながら足していく演算であり

∑(k)　(k：0あるいは1からnまで)

と同じと定義する。

ハテナ演算は総和∑を簡略化したもので
whileに対するforのように、記述が簡素になる分、条件のオプションに制限が出る。
「nから」は指定できるが、「1または0まで」の部分は問答無用に設定される。

＝＝＝＝＝＝＝
これ以外の記号は実在のもので、組み合わせ記号nCmを用いて
(n-1)？＝nC2

が成立する。
nC2は階乗！を用いてn!/(2!(n-2)!)
と書くことも出来るし、
総乗Πを用いて
1/2×Π(k)　(k：n-2からnまで)


また、多項式を用いて

(n-1)？＝nC2＝n(n-1)/2

の恒等式が成り立つ。


（1角形＝点かもなら0本
2角形＝線分かもなら1本）
n=3角形なら3本
四角形なら6本
五角形なら10本
六角形なら15本
七角形なら21本
八角形なら28本

にほんブログ村

JAD：きょうの、ていり。～年度末バージョン～

閏年の前年の大晦日と、年度末日の曜日は同じ。

例：2011/12/31(土曜日)　2012/03/31(土曜日)
例：1915/12/31(金曜日)　1916/03/31(金曜日)
例：9987/12/31(木曜日)　9988/03/31(木曜日)




病院の待合室でふと気づいた定理っす。
2011年度末と2012年度初めはカレンダーの左右どっちか端がスッキリしてるなぁと
あれ、そういえば2011年の年　末と2012年の年始にも似たようなことがなかったっけ？
って考えていて
そういえば去年のクリスマスがリア充向けだったのを思い出し
そういやクリスマスあたりには例年通り、クリスマスと大晦日の曜日の話をしたなぁ
って思い出し
じゃあ31(1月)+29(2月)+31(3月)っていくつだ？って計算してたら
ちょっきり91日なんすよ！91日つったら13週間、つまり丸々1クールじゃないですかぁ！


じゃあこういう定理もありそうですよね

「冬アニメは1クール13話の尺がない。」
年始番組で1週間は潰されますからね
その上、平年だと2月は28日しかないですし。






にほんブログ村

ZYC：割り切れてるようで割り切れない事実が

どうか驚かないで聞いてほしい
僕、これから世界一酷いことをいうよ

円周率が約3.14じゃなくて、ちょっきり3.014だったら11の倍数なのになぁ


小数が整数の倍数！？おかしいだろ！

90分=1.5時間の倍数の睡眠時間を取りなさいってのと同じくらい変に見えるかもしれないけど
それは偏見であって屁理屈ではないんだ。
ところで、へんけんとへりくつを変見と偏理屈って書くんだと思ってたんだよ！驚愕の新事実！





ひとつだけわからないことがある
どうして阿良々木の一人称が僕で、夏目の一人称が俺なんだ？
あらかじめ入れ替わっておいたのか？
まるで怪奇現象って名前の人が妖怪にぶら下がってフライングヒューマノイドってるくらい奇妙な話だな！

にほんブログ村

YWC：思い出したかのように今日の定理～センター図形編～

センター試験

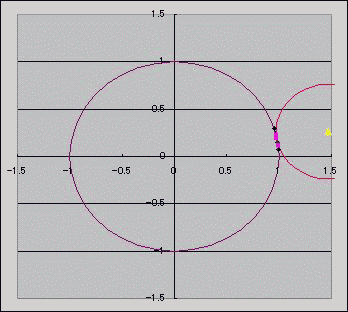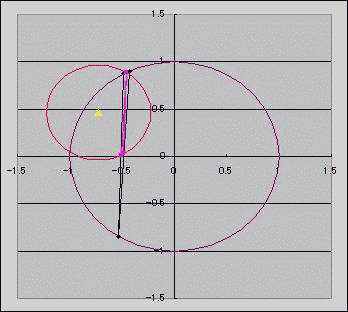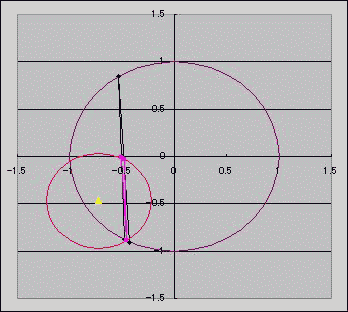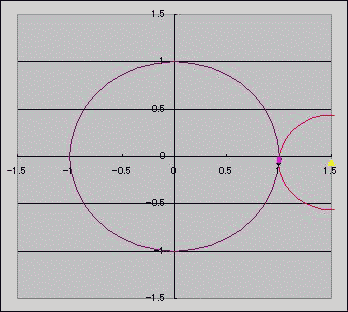三角形ABCに外接する円O1の半径は
三角形ABCの3つの辺の中点からなる三角形DEFに外接する円O2の半径の

2倍らしい。常にな！





_{いちおう、このグラフを描く際に、ベクトルを半分にしたり傾斜を計算したり、
傾斜を垂直にするために逆数を取って符号を反転したり、
直線の方程式を求めるために切片を求めたり、
求めた直線の式から連立方程式立てて行列方程式にしてから逆行列を列ベクトルにかけて連立方程式を解いたり
ベクトルの絶対値を求めたり、かなり力技だったと我ながら思うんだけど
なんかこうもっとエレガントな萌える方法が、あるはずだとは思うんだよなたぶんなぁ。
まあ、総動員レベルで考えるならこれはこれでエレガント萌えるかもしれない。
htmlにはネストできるものとできないものがあるみたいだ。
・図の代替テキストにルビをつけようと思ったらはねられた。(アルト系？)
・でも振り仮名にだけリンクを貼ることはできる。
さて、背景と同じ色にしてタイトル直下に強調で書いた「センター試験」という言葉はブログ村に認識されるのかぁー！？}



正弦定理･･･？まあ、ググったことはあったけども･･･。

にほんブログ村

HSC：昨日の「今日の、定理。」のつづき

2011年11月4日の日記：今日の、定理。～2の自然数乗(2のべき乗)の倍数の見分け方～

を使うと、　65536が「2の16乗=65536」の倍数である　ことを見分けることができる。


まず
○下1桁が偶数で「あれば」65536は偶数;

次に
○下2桁目の3が奇数なので、下1桁が4の倍数で「なければ」4の倍数;

○下3桁目の5が奇数なので、下2桁36が8の倍数で「なければ」8の倍数;

○下4桁目の5が奇数なので、下3桁の536が16の倍数で「なければ」16の倍数;

○下5桁目の6が偶数なので、下4桁の5536が32の倍数で「あれば」32の倍数;

○以降、下6～16桁目は0で偶数なので、下15桁が65536の倍数で「あれば」65536は65536の倍数;

(
下6桁目=0→65536＝64の倍数なので65536は64の倍数;
○下8桁目=0→65536＝128の倍数なので65536は128の倍数;
○下8桁目=0→65536＝256の倍数なので65536は256の倍数;
○下9桁目=0→65536＝512の倍数なので65536は512の倍数;
○下10桁目=0→65536＝1024の倍数なので65536は1024の倍数;
○下11桁目=0→65536＝2048の倍数なので65536は2048の倍数;
○下12桁目=0→65536＝4096の倍数なので65536は4096の倍数;
○下13桁目=0→65536＝8192の倍数なので65536は8192の倍数;
○下14桁目=0→65536＝16384の倍数なので65536は16384の倍数;
○下15桁目=0→65536＝32768の倍数なので65536は32768の倍数;
○下16桁目=0→65536＝65536の倍数なので65536は65536の倍数;
)



ちなみに、2の自然数(0か1以上の整数)乗で「割り切れる」のは2×5=10進数なら整数全部(たぶん全複素無理数まで拡張可能)。





boolean　function（実用例？int n）：
if(196608が65536の倍数かどうか){
true ○下1=8：偶数;
＆＆
true ○下2目＝0：偶数→下1：mod(8,4)=0;
＆＆
true ○下3目＝6：偶数→下2：mod(608,8)=0;
＆＆
true ○下4目＝6：偶数→下3：mod(6608,16)=0;
＆＆
true ○下5目＝「9：奇数」→下4：mod(96608,32)「≠0」;
(false ×下5目＝「9：奇数」→下4：mod(96608,32)「＝0」;)
＆＆
true ○下6目＝「1：奇数」→下5：mod(196608,64)「≠0」;
(false ○下6目＝「1：奇数」→下5：mod(196608,64)「＝0」;)
＆＆
true for ( ○下7～16目＝0：偶数→下6～15＝196608、mod(196608,65536)=0);

return true;
}

ついでに、9と18と6があるので196608は3の倍数


ぷ、ぷろぐらみんぐなんて･･･ぜんっぜん好きじゃないんだからねっ！
ちょっと不意に真が挿しただけなんだからね！(CV：罰金バッキンガム)


にほんブログ村

VRC：今日の、定理。関数のみじん切り編

関数の横千切りのことを量子化
縦千切りのことを標本化(サンプリング)と呼び
両方あわせてみじん切りにして、はじめてデジタル量になる。


ちなみに標本化は空間に対しても時間に対してもできるし
フーリエ空間自体の標本化も可能。
こっちの世界での標本化はあっちの世界での周期化
こっちの世界での周期化はあっちの世界での標本化に相当する。
両方の世界を標本化すると自動的に両方の世界が周期化するし
両方の世界を周期化すると自動的に両方の世界が標本化する。
いわばインパルス列のような感じになるということだ。




そういえば、X線回折のことを習ったときに
「なんでレントゲン撮るときにフーリエ空間で撮影せにゃならんの？」
って思ったときがあったがあれはまったく別問題だった。

小さいものを見るときにフーリエ空間が役に立つよっていう意味であって
別にX線に限った観測じゃなくて
なんでもかんでもちっちゃいものを見たかったらフーリエ空間使ったらお得だよって意味だった。


べ、べつにフーリエ空間は横軸の逆数をただ取ったわけじゃないんだからねっ
そそそれに･･･縦軸とか横軸とかが対数かどうかなんてどうでもいいんだからね！

にほんブログ村

TQC：今日の、定理。(一筆書き)

１．つながってる線で、交差点全部に入り口と出口があれば、一筆書き可能。

２．１の例外として、奇数本出てる交差点は1対まで認める。
このときの書き方は、入り口から出口に向かえばおｋ



JIN：入り口と出口は同じじゃないねん

にほんブログ村

LQC：今日の、定理。拡張版

000～999までの整数のうち、9の倍数112個は
2重複(24個)･･･009、171、855など
3重複(4個)･･･000(999)、333、666
0つ飛び(24個)･･･8と0(9)と1、2と3と4、5と6と7の組み合わせ
1つ飛び(24個)･･･7と0(9)と2、1と3と5、4と6と8の組み合わせ
2つ飛び(12個)･･･6と0(9)と3の組み合わせ
3つ飛び(24個)･･･5と0(9)と4、8と3と7、2と6と1の組み合わせ


のどれかに必ず分類され、9の倍数を含まない2重複以外は必ず真ん中に3の倍数が入る。

また、9の倍数を含まない2重複の18個は、3で割って1余る数の連続と、3で割って2余る数の連続に分類され
それぞれ9つずつ存在する。
3で割って1余る数の連続は1と4と4、4と7と7、7と7と1の組み合わせだけからなり、必ず、3で割って1余る数が2つと、それより3つ少ない数1つで構成され
3で割って2余る数の連続は5と2と2、2と8と8、8と5と5の組み合わせだけからなり、必ず、3で割って2余る数が2つと、それより3つ多い数1つで構成される。


なお、9の倍数なので、8の次の9を0としている。

数	分類
117	2重複(3で割って1余るシリーズ)
144	2重複(3で割って1余るシリーズ)
171	2重複(3で割って1余るシリーズ)
414	2重複(3で割って1余るシリーズ)
441	2重複(3で割って1余るシリーズ)
477	2重複(3で割って1余るシリーズ)
711	2重複(3で割って1余るシリーズ)
747	2重複(3で割って1余るシリーズ)
774	2重複(3で割って1余るシリーズ)
225	2重複(3で割って2余るシリーズ)
252	2重複(3で割って2余るシリーズ)
288	2重複(3で割って2余るシリーズ)
522	2重複(3で割って2余るシリーズ)
558	2重複(3で割って2余るシリーズ)
585	2重複(3で割って2余るシリーズ)
828	2重複(3で割って2余るシリーズ)
855	2重複(3で割って2余るシリーズ)
882	2重複(3で割って2余るシリーズ)
9	2重複(9の倍数含む)
90	2重複(9の倍数含む)
99	2重複(9の倍数含む)
900	2重複(9の倍数含む)
909	2重複(9の倍数含む)
990	2重複(9の倍数含む)
0	3重複
333	3重複
666	3重複
999	3重複
18	プラス1
81	プラス1
108	プラス1
180	プラス1
189	プラス1
198	プラス1
234	プラス1
243	プラス1
324	プラス1
342	プラス1
423	プラス1
432	プラス1
567	プラス1
576	プラス1
657	プラス1
675	プラス1
756	プラス1
765	プラス1
801	プラス1
810	プラス1
819	プラス1
891	プラス1
918	プラス1
981	プラス1
27	プラス2
72	プラス2
135	プラス2
153	プラス2
207	プラス2
270	プラス2
279	プラス2
297	プラス2
315	プラス2
351	プラス2
468	プラス2
486	プラス2
513	プラス2
531	プラス2
648	プラス2
684	プラス2
702	プラス2
720	プラス2
729	プラス2
792	プラス2
846	プラス2
864	プラス2
927	プラス2
972	プラス2
36	プラス3
63	プラス3
306	プラス3
360	プラス3
369	プラス3
396	プラス3
603	プラス3
630	プラス3
639	プラス3
693	プラス3
936	プラス3
963	プラス3
45	プラス4
54	プラス4
405	プラス4
450	プラス4
459	プラス4
495	プラス4
504	プラス4
540	プラス4
549	プラス4
594	プラス4
945	プラス4
954	プラス4
873	プラス4
126	プラス4
162	プラス4
216	プラス4
261	プラス4
378	プラス4
387	プラス4
612	プラス4
621	プラス4
738	プラス4
783	プラス4
837	プラス4

鍋頭6:39

にほんブログ村

ZPC：32ビットとかの今日の定理に追記

9月11日づけの「今日の定理」にベン図とカルノー図を追加しておいた。



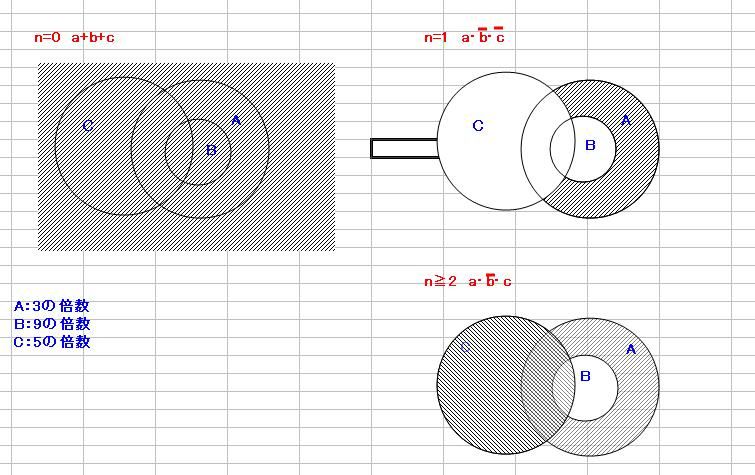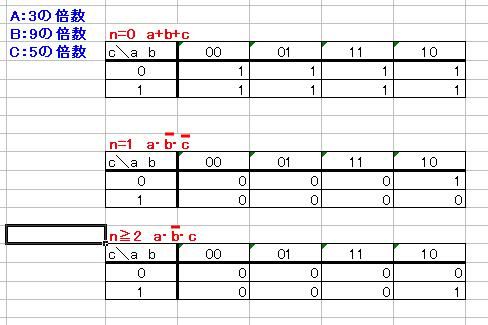あんまり意味はなかったりする



今回の日記がなんとなくビジュアル系だったので、
ブログ村へのリンクもなんとなくビジュアル系

にほんブログ村

LPC：感動した！

1734を17で割ったらなんか感動した！

素の元の数	17	×	102	=	1734
9で割った余り	8	×	3	=	6
備考use	1+7=8		1+2=3		1+7+3+4=15、1+5=2+4=6

元の数を9で割った余り同士でも掛け算が成立してるなんて感動以外の何者でもない！




気づいたけど、空想するのはほとんどタダだけど厳密には微妙にタダじゃないですよね
脳を動かす食費とか、紙代とか消しゴム代とか鉛筆代とか、ケータイの充電気料金とか。

にほんブログ村

ZOC：今日の定理に再追記

9月11日付けの「今日の、定理。」シリーズに以下を追記。

(2^(2^n))-1=Π((2^(2^k))+1)　(k：0～n-1)
特にn≧1なら直積(総積)Πに(2^(2^0))+1=3を含むので3の倍数
n≧2なら直積Πに(2^(2^1))-1=5を含むので5の倍数



今日のマッドオカルティスト

にほんブログ村

OOC：追記した

9月11日付の「今日の、定理。」シリーズに追記した。


「人間は考える良し悪しである」
ヨシもアシも漢字で書けば葦だからなぁ

にほんブログ村