|
20080511～
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
フーリエ級数展開はボールはともだちみたいな感覚なんですが
フーリエ変換については実は苦手意識があります。 なんか飛躍しすぎ感しませんか フーリエ級数からフーリエ変換に至る際に、「実係数の複素化」と、「周期・離散の無限・連続化」の両方を同時にやったからわかりにくいんだと個人的には思うんですが。 フーリエ変換の実数バージョンがあればいいなぁ(中間形態その２) と思って実フーリエ変換でぐぐったらサジェストするんですが 「フーリエ変換」のwikipediaにおまけ程度に載っているだけで それが僕の探している実フーリエ変換なのかどうかよくわからない・・・ なんとなくコレジャナイ感がするんですが。 「月を大きく見せる」のメモを「胸を大きく見せる」に見間違えた。 いや、案外遠近法でなんとかなるかもしれない ちなみに寄せて上げるとこうなるそうです  にほんブログ村
PR
めっちゃ久しぶり！
前にフーリエ級数展開をしたときは、確かアニメの「日常」をやっていて(Eテレ以前) EDの「Zzz...」に出てくる蛇を描こうとして試行錯誤するも、結果オーライで描けた そのくらい前だったと思います。２０１１年４月～９月ってことは・・・もう３年以上前の事になるんですね 野暮用で、デューティ比を考慮したパルス波をやってみたんですけどね それと、群速度と位相速度についての計算も久しぶり！ そうそう、たぶんここが引っかかってたんだと思います。 シュレディンガー方程式に従った自由粒子の群速度は位相速度の２倍あって なんで位相速度のほうが遅いの？ っていう疑問を以前も抱いたことがあったような気がします。 一概に位相速度のほうが速いとも言い切れない、とかそういう理由じゃなかったかな。 群速度がホンモノの速度とも言い切れず、エネルギー速度とかいうのがあったような気も。。。  にほんブログ村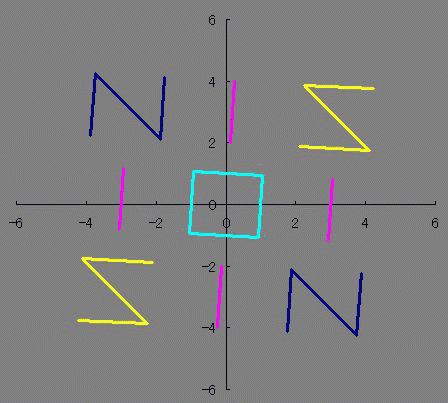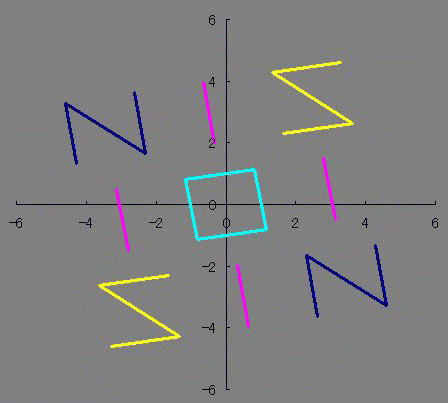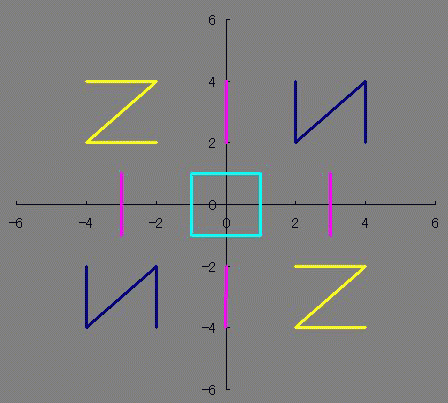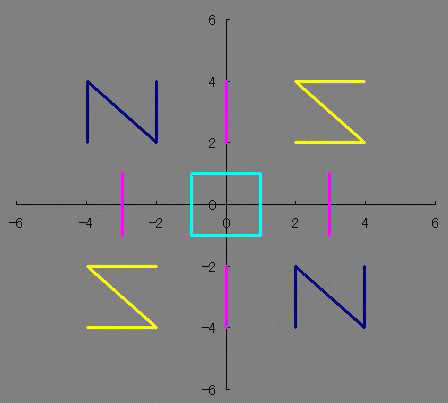
 整数は必ず偶数か奇数に分類されるのに 関数は必ずしも偶関数か奇関数に分類されるわけじゃないですよね どちらでもない関数もあれば、 どちらでもある関数もあります たとえばy=0は偶関数でも奇関数でもありますが 他にも有るんじゃないだろうかと、条件を整理してみますと ただ単にx(横)軸対称でありさえすれば偶関数でも奇関数でもあるということがわかります。 NIS IOI SIN 西尾維新 さんは惜しかったね！ 楕円とか双曲線とかがそうですね あんまり話題にされないのかな？ 偶関数でも奇関数でも「ない」関数のほうが話題になってる気がします ググる際に「楕円関数≠楕円の関数」と「双曲線関数≒≠双曲線の関数」 というネーミングも邪魔をしているのでしょうか ところで 偶関数×偶関数や偶関数×奇関数、奇関数×奇関数が楕円や双曲線でどのようになっているのだろうと気になりまして 実際に掛け算してみました。 楕円の式は 双曲線の式は ですが、2種類の双曲線のうち今回使いたいのはy軸対称ではなくx軸対称のほうなので (x/a)^2-(y/b)^2=1のみ使います のうち、1つ目の複合はx軸対称であるために重要なものですが 2つ目の複合は後述しますがぶっちゃけ必要ありません プラスだったら楕円、マイナスだったら双曲線です。 楕円×楕円をやってみましょう。究極の同性愛です。 2つの楕円でa、bが異なるとします。 のy1×y2をやってみましょう。 y=y1×y2 になると思います。 次に、双曲線×双曲線をやってみましょう。 これも、楕円×楕円と同じ結果 になることがわかるかと思います。 グラフはこんな感じです。 （偶関数＆奇関数）×（偶関数＆奇関数）は、やっぱり偶関数＆奇関数の両性具有だということが判明しました。百合×百合＝ホモ×ホモ＝ふたなり だったというわけです。 しかもシスコン・ブラコンの属性も有ることがわかりましたね！とんだ変態でした。 楕円×双曲線はどうでしょうか これは実数にはなりません 双曲線は楕円の外側にしか値を持っていないので、掛け算するとどうあがいても値を持てないのです。 だから2つ目の複合±は意識しなくても良いということなんです。＋×＋＝－×－になって、＋×－が存在しないわけですからね しかしながら、楕円×楕円と双曲線×双曲線がイコールで結ばれたことはちょっとした驚きですね 一度数値として出力してから掛け算してたら気づかなかったかもしれないところです。 ビバ解析計算！ それにしてもファインマン・ダイアグラムに見えて仕方がないです まあExcelだと「空白ではない非数値」をゼロと描写してしまうからなんですが。 （偶関数＆奇関数）×偶関数 や （偶関数＆奇関数）×奇関数 はどうなるでしょうか 結果はこれらもまた（偶関数＆奇関数）に収束してしまいます。 y=0になにかけてもy=0になるのと辻褄が合いますね。関数ホイホイというわけです。人類ふたなり化計画のようですね  にほんブログ村
ペロンフロベニウスの定理
日本語でおｋ ってことで可視化してみました。 0～1の擬似乱数を3行3列の行列にぶち込んでます。(赤いほど大きく、緑いほど小さいように色分けしてます) この「中身が必ず正の実数」な非負行列Aに対して、複素数の固有値候補λを用いて行列式 det(A-λE)=0 の固有値方程式をλに対して解きたいわけですが、n行n列だと一般にn次方程式になりますよね。 そこで、det(A-λE)の絶対値をプロットして、そのゼロ点を探ってみることにし 条件付き書式と、マトリックス方式を使った3D描画でabs(det(A-λE))のゼロ点を探ることにしました。 λ=x+iyとして、基本的に横xを実軸、縦iyを虚軸としてます。 乳首色をしてる辺りがゼロ点です。 そのままだとあまりいいかんじに炙りだされないので、abs(det(A-λE))を指数関数に入れたEXP(||A-λE||)で誇張表現してます。 (3行3列のAにしたのはサラスの方法でサボりたかったからです) 見事に、右寄り横長になりましたね。これがペロンフロベニウスの定理の言いたいことの１つのようです。 今回は3次方程式なので、複素解も含めると一般に3つあるわけですが 非負行列の固有値は「絶対値の一番大きな解が必ず正の実数」ということですね。 これは便利。 なんでかといいますと フィボナッチ数列を行列とみなしたときの日記を見てもらうとわかるかと思うのですが フィボナッチ数列って黄金比を比率とした等比数列に漸近していくんですよ。 それと同様に、同じ非負行列Aを何度も何度も掛け算し続けると 正の実数の効果だけが生きのこって繁栄されるというわけです。 （ところで、 残りの固有値は必ず「実数」あるいは「複素共役」になるのかな？？固有積である行列式も非負実数だろうし：4次以上じゃないとなんともいえないかも） それはそうと、ちょっとずつ違った非負行列Aが100個くらいあって A1～A100まで全部掛け算したらどう近似されるんだろう？ ってのは、結構みなさん気になりますよねたぶん。 気が向いたら調べてみます。 よかったらExcelDLファイルでも遊んでやってください＾＾ expに打ち込んだらゼロ点はイチ点になりますよね・・・ にほんブログ村 ※追記 実対称非負行列の固有値ｗｗｗｗコンボ縛りすぎわろたｗｗ
大学の時に制御のおっさんが言った
制御で使うのは○○行列だけだから、固有値も△△なんだよ。安心してね の○○が実数・実対称だったのか、あるいは非負だったのか、思い出せないんですよね。 ペロンフロベニウスの定理っていうらしいんですが ちょっとまだよく読んでないんでそのうち読みます  にほんブログ村 正定値行列のほうだったなかぁ？あれ？正定値ってエルミートに近いものなの？
昨日、リニアングラフ3dというツールを試しに導入してみまして
そこで知ったんですが、 Asin(2π(√(x^2+y^2)/λ-ft)) こういう描画方法をマトリックス方式 こういう描画方法を3カラム方式 と、呼ぶらしいです。 名前があると便利ですね！ ただ・・・あまり浸透した名称ではないような気もします。 なお、マトリックス方式のデータをコピペーではなくカッペーしてそのまま3カラム方式に流用している関係で、ラインかメッシュ、どちらか片方をサボっています。 いつものごとく、delボタン連打りんぐか押しっぱなしで再計算するので、動きます。 それと、DLエクセルファイル  にほんブログ村
一対一対応なんですかね？
1つのエルミートを対角化する際に1つのユニタリが作れるわけですが。 (あー・・・固有値が重解だったら僕はいまいちよくわかってませんが) でも2行2列の回転行列も対角化できそうですよね エルミートではない実数行列のユニタリを対角化する際にできる2次的なユニタリ・・・？？ 「ユニタリで対角化」ではなく「ユニタリを対角化」。しかも2×2実数という極めて限定的なユニタリ。 それともこれは、パウリ行列の実数な基底に分解されるから、結局エルミート行列を相手にしてるってスタンスには変わりはないのかな？？？つまり反例にはならない？  にほんブログ村 プールの水面に映る虹色の波紋が光の分散によるものなのか気になって仕方がない 温泉のときから気になってた！でも温泉はのぼせるからあんまり入ってられなかったんだよ！！！
仮説の段階なのでまだなんともいえないアレなんですが
ここんとこ忘却力がパないので備忘録をということで。 意欲の忘却力もパネエ！ 俺んちの比熱いくらよ！？ 以前、グルーオンのことを調べた際にゲルマン行列というものに出会いまして ちょっと背伸びして、五目ゲルマン行列可視化器を作ったのはいいものの そんときは8つのゲルマン行列λ1～8を指数の中にぶち込んだ行列指数関数のオイラーの公式ver まあいわゆるユニタリ行列が exp(∑(iλnθn))=Πexp(iλnθn) の関係にあるとは限らない っていうのにまるで気づかずにおりまして それでもユニタリ行列なら固有値が複素単位円という1次元のようなものの上に現れるから きっと等号が成立するんだろうと信じていたのですが いざ一段簡素なパウリ行列でやってみようとしたら これがまたうまくいかないことがわかりまして でもここでふと疑問に思ったのが いくら複素行列でも2行2列のユニタリ行列の固有値は最大で2つしかない ということなのでした。 3次元の回転なのに2つしかないのです。 ということは、どう回転させようとも、結局は2つの回転行列の積で表すことが可能なのではないか！？ という期待に満ちた仮説を思いつきまして 確かにヒンジにもう1つヒンジを付け加えたら、どの向きも向けそうじゃないですか。 それに、昔から言われてるジンバルロックという現象も この「3次元の回転なのに自由度が2つしかなかったりする」ことに由来するのではないか と思われるわけでして さらに、3次元の極座標の取り方には直交座標ほど唯一無二の取り方なんかない というのを加味すると これはもしかして、待望の 任意軸での回転(主にクォータニオン)を2つの回転行列の積に還元できるのではないか！？ というなんとなーく期待めいたアレについに行き着くのではないか そんな仮説を抱いているのです。 今はさほど具体的ではないのですが 線形独立な軸回りの回転行列U1とU2があって U=U1U2の固有値と 任意軸回転の行列Mの固有値 何らかの方法でこれさえピッタリと合わせることができれば お互いに変換可能なのではないか というものなのです。 たとえばコレ 2つの回転行列U=U1U2を使って六角形(エディントンのイプシロンorレビチビタ記号)を真正面に向かせましたが 斜めの回転軸Mを使うことで、一発回転で真正面を向かせることも可能じゃないですか この2種類の回転行列RとUの固有値はもしかして一致するのではないか！？ という仮説です。 ことごとく真実に裏切られてる最近ですががが。。。 具体的な計算過程を示す余裕がなくて申し訳ない 最近体力がですねｒｙ  にほんブログ村
２×２の正方行列だから
固有値はいつも２つ以内 これは何を意味するんだろう？ ３次元回転は２軸の複合回転に還元可能ってこと？？ 線形独立なヒンジが２つあれば、どの向きも向ける？？ これがパウリ行列じゃなくてゲルマン行列だったら ８次元みたいな空間の回転でも、結局は３軸の複合回転に還元可能っていう感じ？？ ｎ行ｎ列のユニタリ行列に拡張すると ｎ＾２－１次元みたいな空間内の回転は、結局はｎ軸の複合回転に還元可能？？ それはさておき さっさとやんないとな パウリ行列可視化器。 めんどくさいというか、燃える問題に出くわしたというか なんつーかもう。はい。はぁ。。。  にほんブログ村
計算できるっぽいのはいいのですが
前回も言ったとおり、a+biの文字列(各15桁くらい)扱いで表示されてしまうので キャプチャーをどうしたものかとか なんか割とどうでもいいことで悩まなきゃいけないのが辛いです これ表示しなかったら何がしたいのかまるで伝わらないでしょうし 表示のためだけに3桁用のセル用意しちゃろか DLファイルにしちゃえばどうってことないのになんでこんなことで悩まにゃいかんのか。 最大、15桁くらいの実部と、15桁くらいの虚部って先日書きましたが あれ？そういえば小数点以下15桁だっけ？とか思って 有効数字15桁くらいの浮動小数点型だからやっぱり単に15桁でよかったんでした。 σn：nはパウリ行列なら1～3、ゲルマン行列なら1～8、順番に。 ||Π(exp(iσnθn))-λ||=||exp(∑(iσnθn))-λ|| (※ただし、固有値の候補λ=exp(iθ0)) になることを期待してみているんですが 今のところうまくいかないのは論理の支配構造による仕様なのか、単にバグなのか 各θnの範囲を360°周期にしてないあたりがちょっと気になってます。 例によって例のごとく、どうせ三角関数の中にぶち込むんでしょって感覚でnow()-today()に100万とかかけただけでテキトーにやってるので。 θ1、θ2、θ3はいちおう、2：3：5とかな感じで、大きすぎない程度に互いに素にしようとしてます。 θ=√(θ1^2+θ2^2+θ3^2)のRMS取ってるあたりがなぁーなんかやらかしてる気もするんだよなぁー さっさとmod(θ[°],360)してしまおう ところで エルミート行列Aがあって、|A|っつったらdet(A)だし、||A||っつったらabs(det(A))ですよね |A|=abs(A)=A×A†の実対称行列 とか ||A||=det(abs(A)) なんてことはまずないですよね。 まあ、Πと∑が一致しなかったところで、一致しなかったよごめんねてへぺろで済むんですけどね あーそれにしてもやっぱりヤコビ法は習っといたほうがいいよなぁー 自動でやってくれるサービス終わっちゃったし できれば、やっぱり配列関数必要だったわーって、勘違いなりにも一度夢中になって せめてVBAの基礎でも叩き込んでおきたい オブジェクトオブジェクト言っといてVBAがオブジェクト指向じゃないっぽいのがわろてまう そんな自分はオブジェクト指向にまだ躓いてる途中だから余計わろてまう もし抽象クラスかなんかでクォータニオンの演算体系を作れなかったら それこそパウリ行列をクォータニオンの3つの虚数単位代わりとして作ってしまおうかｗｗｗ そういうアホみたいなことするの好き好き人間です 世の中を便利にするついでに技術を学んでるんじゃない！ 技術を学ぶついでに世の中を便利にしてるんだ！！byみつかそうじ そうじ「お前は死んだはずだ！ポニーテール属性の俺の兄貴、みつかそういち！」 そういち「そうだ！私は一度死んでアルティメギルに生まれ変わったのだ！そして長になった！」 そうじ「だったら、俺が亡くしたアルティメギルのお（か）しい人たちを人間に生まれ変わらせて俺の友達にすることも可能なんだよな！？」 そういち「は？なにその超速理解」 そうじ「お互い将棋をやっていればわかることだろう？倒した敵は味方になるんだ」 そういち「倒さなくても俺はいつだってお前の味方だがな」 そうじ「にいさん！」 あいか「将棋とかマジムリ。私の小さな胸筋はそんなルール覚えようとすらしないわ」 とぅあーる「でしょうね～私ほどの胸と白衣があれば、テクのろしーがなんとかしてくれるのに」 あいか「じゃあその白衣のスペアもらった！フゥーハハハ」 とぅあーる「ちなみに白衣もミウラ折りです。あいかさんには畳めますかねえ？」 あいか「白衣は畳むような代物じゃない！くたびれているほうがちょうどいいのよ！」 とぅあーる「そ、それはどもっとも。ぐぬぬ」  にほんブログ村
今日の内容は、先日の日記の中身です。 (エクセルで3D)遠近法の例外処理の話 こいつをやるとき、奥に向かう線が書けなかったのには理由があって このときはまだ 奥行きがカメラの手前にくるとおかしくなっちゃうのを隠す例外処理が 縦線と横線にしか適用できなかったんです。 こういう風に、端から端まで1本のワイヤーで表現してましたからね またそのために、回転にも対応できなかったんです。 横線や縦線がいつ奥行きの線になるかしれなかったですからね そこで、ワイヤーをみじん切りにしてみたんですよ ドモルガンの法則でORをNANDに その上で、 物体の奥行きがカメラよりこっちにきたらxもyも0にしてやる例外処理を施すんですんです。 長さゼロの線をど真ん中に隠しても見えないわけですよｗ そうすることで、奥行き線への拡張も回転対応もばっちりってわけっす。 ちなみに、例外処理をしないとこうなります。 before after というわけで、いつものExcelファイル投下です。 よかったら遊 基本的に枠線より上をいじるといいと思いますし ただデリートボタンを押しまくるだけでもいいですよ  にほんブログ村
長さ0の線分を真正面どまんなかに隠しました 例外処理のためにひたすら線を千切ったら、行数が1000行くらいになっちゃったんすよ＞＜ これを、視野に映る一番手前の線だけ表示とかに工夫したら末恐ろしいことになりそう 今回の作業自体は、ものすごくラッキー・・・じゃなかった計画通りに進みました  にほんブログ村
|
カレンダー
カテゴリー
ブログランキング
ブログランキング参戦中
よかったらポチッとお願いします＾＾
最新CM
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
[03/17 Robertaverm]
最新記事
(01/01)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
(08/04)
(10/24)
(06/08)
(05/22)
(01/13)
(11/04)
最新TB
プロフィール
ＨＮ：
量子きのこ
年齢：
43
ＨＰ：
性別：
男性
誕生日：
1981/04/04
職業：
WinDOS.N臣T
趣味：
妄想・計算・測定・アニメ
自己紹介：
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例：H→7番目、XP→15(P)×26＋23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいｽﾞｺｰ
バーコード
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|
