|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
英語ならどっちもfrequencyですしね
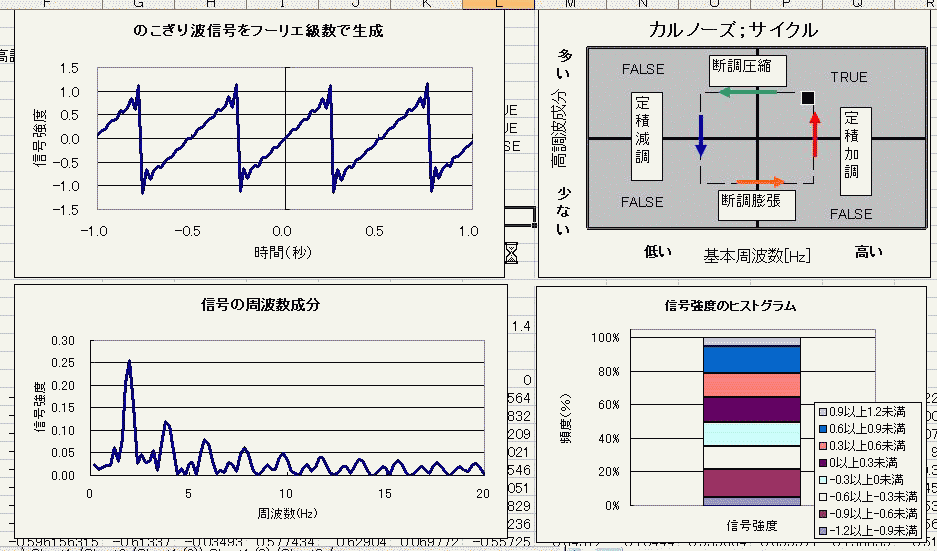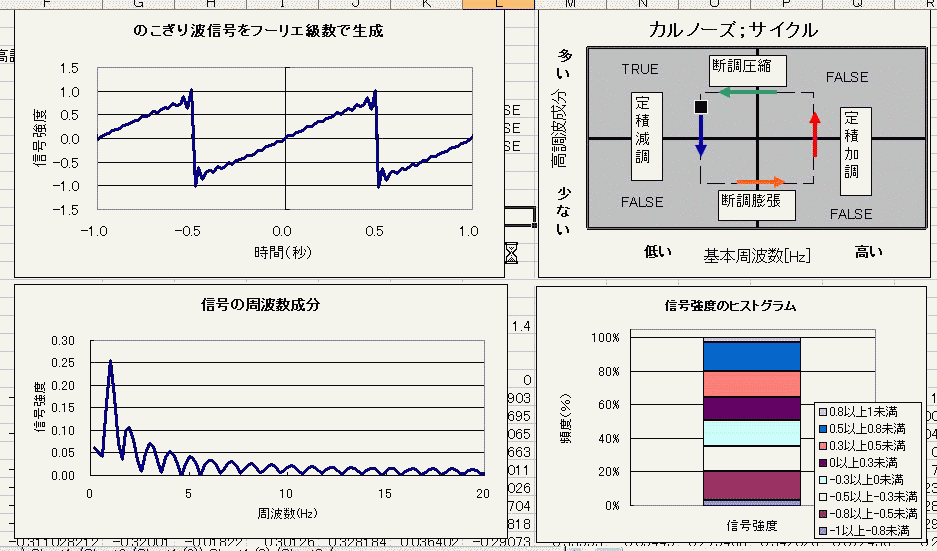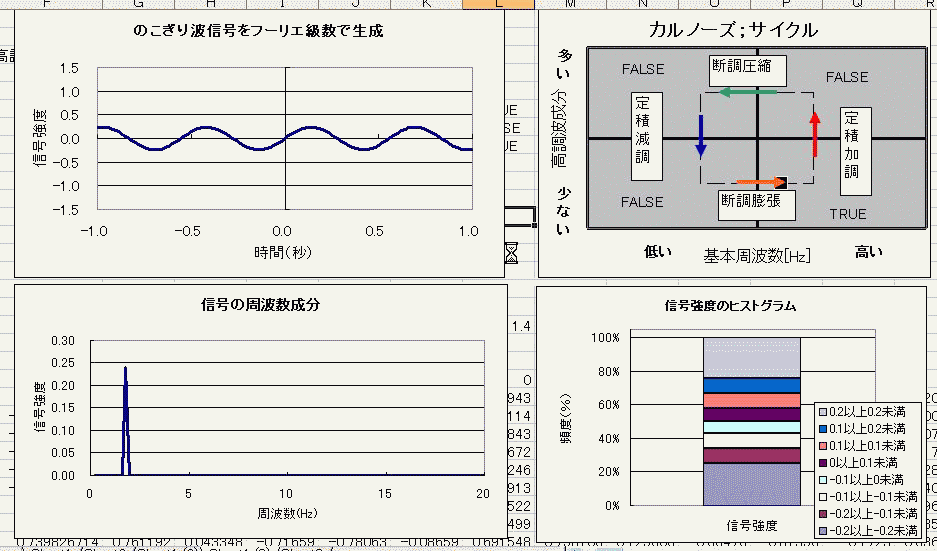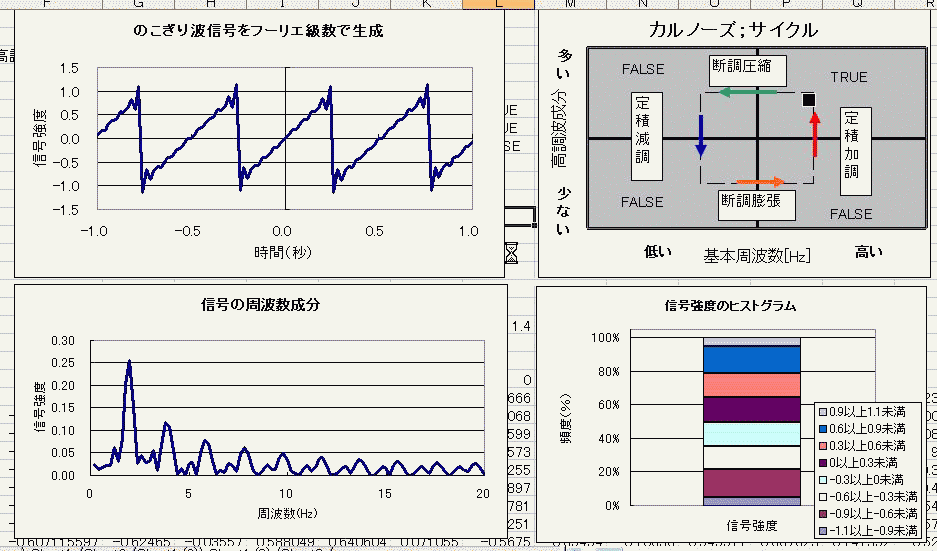 そんなわけで、時間的な関数 今回はノコギリ波をサンプルに 周期と高調波成分がともに変化する際の、フーリエ変換前後のグラフと、信号強度のヒストグラムを並べてみました。 どうでもいいですけど、カルノーズサイクルって書くと、1つの単語として検索されるかもしれないから カルノーズ;サイクルで分けてあげるとカルノーズとサイクルそれぞれでもヒットしてくれるかなー なーんて思いを込めて、シュタインズ;ゲートの間にセミをコロンと死なせてるのかなー とか思ったりしている日々です。^^ まあ割りとこのファイル作るまで紆余曲折ありました 放置期間が主成分でしたけど^^ なんとか完成させられて、よかった。 ただ右上の図でダジャレを言いたい!その一心でこぎつけましたよ!!  にほんブログ村 PR
変換前の逆数だと思っていた時期が俺にもありました。
そうとは限りませんよね>< 例えば、矩形波 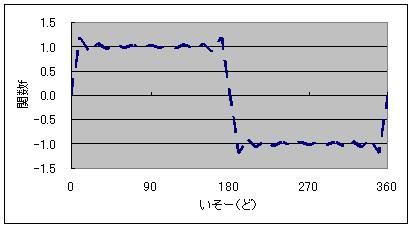 の、フーリエ変換って、別に横軸ヘルツでも秒でもどっちでもいいじゃないですかー 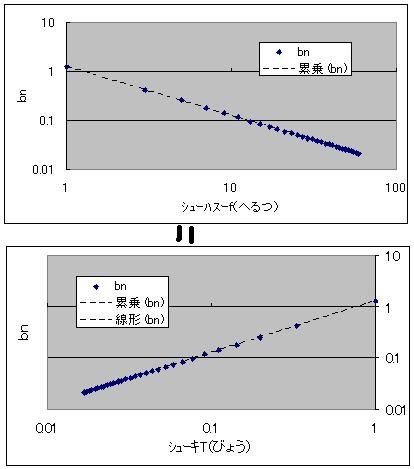 ついでにいえば両対数での比例の近似って、累乗でも線形でもどっちでもいいじゃないですかー 双  にほんブログ村
最近数学ゴリ押し気味ですみません^^おはようございます量子きのこです
さて、ベクトルの内積と外積というものを数学で習いましたよね そのとき、2つの積の定義を習っても、意味合いがよくわからなかった人は多かったのではないでしょうか ベクトルA(xa、ya)とB(xb、yb)があって 内積A・Bと、外積A×Bというのは具体的に何を意味しているのでしょうか。 内積A・Bの定義はこうでした。 A・B=xaxb+yayb そして、それはベクトルA、Bの絶対値|A|、|B|と、AとBのなす角θと A・B=|A||B|cosθ という関係がありましたね。これはどういう意味なのでしょか。 エクセルを起動して、オートシェイプで適当にベクトルを2つ、描いてみましょう 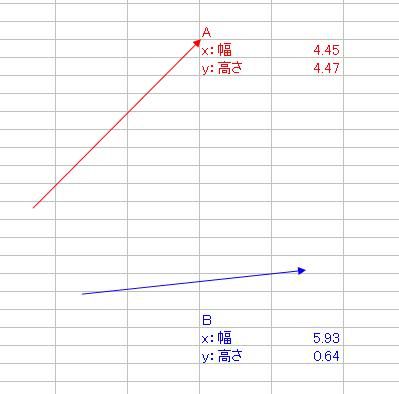 次に、Aベクトルは赤、Bベクトルは青、と色をつけておきましょう ↓ AとBベクトルのサイズをメモしておきましょう 僕の場合は ・A x(幅):4.45、y(高さ):4.47 ・B x(幅):5.93、y(高さ):0.64 とりあえず内積を計算します。 xaxb+yaybなので、僕の場合は4.45・5.93+4.47・0.64=29.2493くらいになりますね それから、とりあえずそれぞれの絶対値|A|と|B|も計算しておきましょう。 絶対値の求め方は、三平方の定理から |A|=√(xa2+ya^2)、|B|=√(xb^2+yb^2) でしたね。僕の場合はそれぞれ |A|=√(4.45^2+4.47^2)≒6.3074くらい |B|=√(5.93^2+0.64^2)≒5.9644くらい それでは、内積A・Bを2つの絶対値|A||B|で割ってみましょう。 A・B/(|A||B|)≒29.2493/(6.3074・5.9644)≒0.77794 これが、実はAとBのなす角度θのコサインだという関係がありましたね。 そこで、AとBのお尻同士をくっつけます。 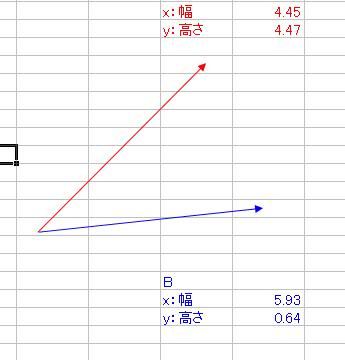 それから、角度を測るために、真四角をベクトルのお尻に添えます。 真四角を少しずつ回転させていって、ベクトルBのお尻にくっつけます。 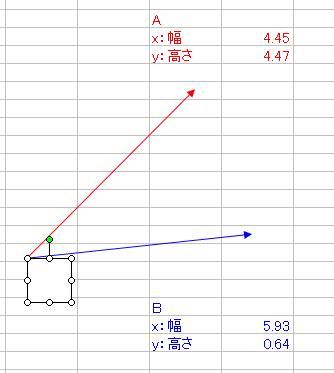 → →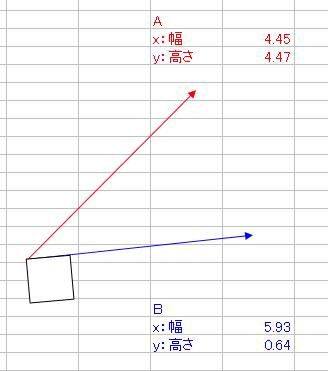 そのときの角度、僕の場合は355度が、Bの角度です。 次に、真四角を複製して、Aのお尻にもくっつけて角度を測ります。 僕の場合は315度が、Aの角度でした。 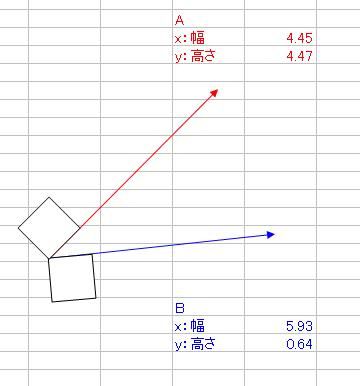 それでは、AとBの角度の差はいくらでしょうか。僕の場合は355-315=40度ですね。 これをθとして、cosθを求めると・・・(※ただし、コサインに入れるのはラジアンに限る) cosθ≒0.7660くらい 精度は悪いですが、0.8近い0.7で、内積A・Bを絶対値|A||B|で割った値とだいたい合ってますね! ======= 次に、外積の意味合いを説明します。 AとBの外積A×Bはxayb-yaxbでしたね。 これは何を意味するのでしょうか。 ベクトルAのお尻をベクトルBの頭にくる  ようにコピーしてから平行移動させてみましょう。 ようにコピーしてから平行移動させてみましょう。同様に、ベクトルBも、お尻がベクトルAの頭にくる  ようにコピーしてから平行移動させてみましょう。 ようにコピーしてから平行移動させてみましょう。平行四辺形ができましたね。 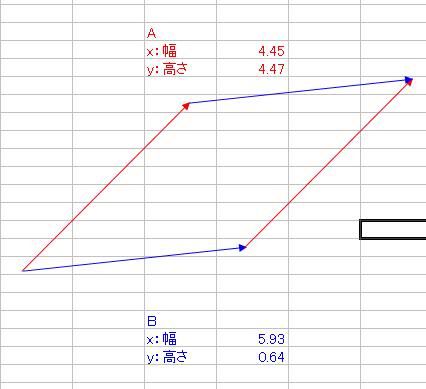 外積A×Bは、実はこの平行四辺形の面積です。 平行四辺形を長方形に変形させて、確認してみましょう。 左側のベクトルAから、水平に線を引きます。 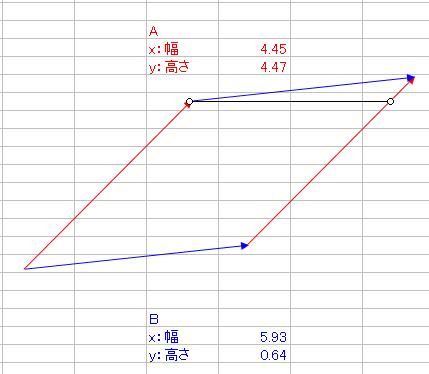 この水平線を、元々のABのお尻に合わせ、 ベクトルAの傾きをそのままに、下の水平線から生えさせます。 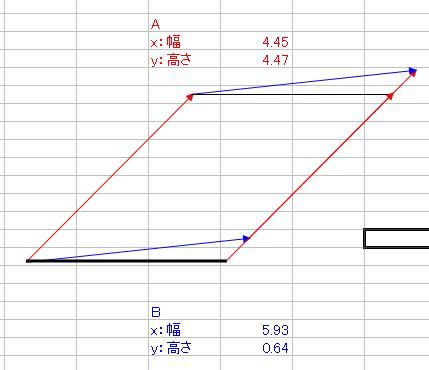 → →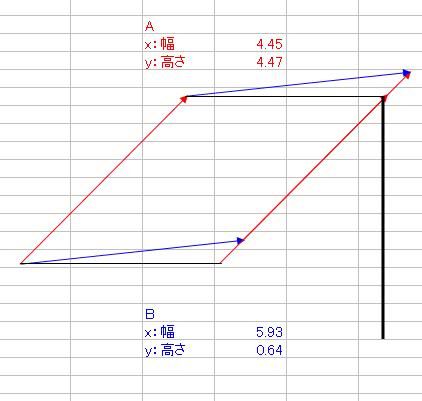 → →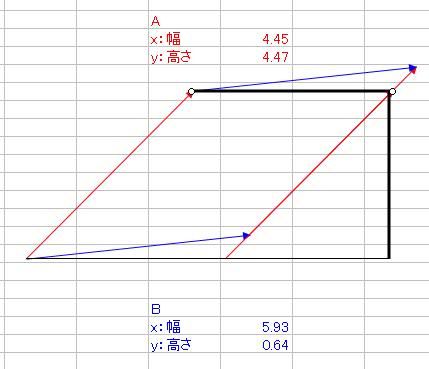 次に、上側の水平線の右側から、 下側の水平線と垂線の重なるところまで垂線と ここで、垂線と上側の水平線の長さをかけたものが、平行四辺形の面積になるので、 長さを測ると、 A×Bと比較しますと A×B=23.6591くらいと、だいたい合ってることがわかりますね。 ただ、A×Bをそのまま計算しますと、マイナスの23.6591になっていることがわかります。 このマイナスは何を意味するのかといいますと、AとBのかけた順番を意味しています。 B×Aの符号、といいますか向きはA×Bの符号と逆になります。 どういうことかといいますと 外積はベクトル積とも言って、スカラー積つまり内積のA・Bとは違って、計算されたものがベクトルになるんです。 一見スカラーのように見えるのは、平面内で外積をやっているからで 画面の手前から奥、あるいはその逆に向かっている成分だけがスカラーのように計算されているだけなのです。 外積A×Bの意味するところは 大きさはAとBが作る平行四辺形の面積 向きは、A×Bとした場合は、AからBに向けて回転する向きと右ネジ(右手)の関係の方向 というものなのです。 今回はA→Bが時計周りだったので、ネジを右に回したら奥に進むように 画面の手前から奥に向かうベクトルとなりました。 ではどうしてこれがマイナスを意味するのかというと 座標系の定め方(約束事)が関係してきて 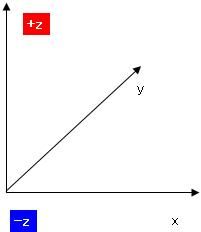 x軸からy軸に向けて回転する方向と右ネジ(右手)の関係に、z軸のプラス方向を定める と公に約束しているからなのです。これを右手系と言って、 z軸の±が逆向きの左手系よりも右手系のほうを一般的には多用します。 今回の外積は、z軸のプラスの向きと逆向きだったので、外積がマイナスの値になったのです。 ちなみに 3次元空間でベクトルA(xa、ya、za)とB(xb、yb、zb)の 外積をする際にはx、y、z軸の単位ベクトルi、j、kと、 行列C=
A×B=|C|と、効果的に覚えられます。  にほんブログ村
ここ最近、循環参照ゴリ押し気味ですみませんが、マイブームなので生暖かい目で見守ってやってくれれば^^;
まずは、速度の1乗に比例した空気抵抗を受けながら落下する物体(質点)の運動をシミュレートしてみましょう 運動方程式はこうでしたね。 F=ma F:力、m:質量、a:加速度 加速度aを速度vの時間微分としてみますと a=dv/dtなので、運動方程式は F=mdv/dt になりますね。 では力Fはどうなるかといいますと、今回は速度の1乗に比例した空気抵抗を受けながら重力落下するという条件なので、 速度の向きを鉛直下向きに取って F=mg-rv となりますね。g:重力加速度、r:空気抵抗 ですから、運動方程式は結局 mdv/dt=mg-rv となります。 しかしながら、これではエクセルさんが困ってしまうので、微分を差分に翻訳してあげましょう。 dv→Δvなので、v2-v1 dt→Δt つまりdv/dt→(v2-v1)/dtとなるわけです。 これを運動方程式に当てはめますと m(v2-v1)/dt=mg-rv2 になりますね。 これをv2についての式にまとめなおしますと v2=(v1+gdt)/(1+rdt/m) になります。  これを、図の速度vのところに入れてやります。 v=IF(sw,(v1+gdt)/(1+rdt/m),v0) sw:初期化スイッチが0(オフ)のときはvの初期値v0を維持し 1(オン)になったら循環参照を開始して vのセルに(v+gdt)/(1+rdt/m) を代入する、という意味です。ここでvは自分自身のセルなので循環参照しています。 循環参照を開始する際に、ツール→オプション→計算方法→反復計算にチェックを入れ 反復計算回数を1にしておきましょう。変化の最大値はデフォルトの0.001で構いません。 dt=0.5、m=100/g(mg=100)、r=1、初期速度v0=0としておき 反復計算開始スイッチswを一旦0にしてから1にして、delでも押しっぱなしで再計算し続けると  速度vが0から終端速度vlast=mg/r=100に漸近していくのがわかりますね、わかります^^ ========= では次に、2階の微分方程式に挑戦してみましょう。 力が距離に比例する振り子を例に取ります。 運動方程式はmdv/dt=Fでしたね。 今回このFは、距離xに比例してxとは逆向きに作用する力ですので F=-kxと置くことにします。 ここで、距離という変数が出てきたので、速度と距離の関係を使って距離を定義すると 速度は距離の時間微分なので dx/dt=v でしたね。 この2本の連立微分方程式 dx/dt=v mdv/dt=-kx を差分の形で解くことが 2階の微分方程式d^2x/dt^2=-kxを数値解析で解くことに相当します。 dx/dtも先ほどと同様に微分から差分の形にすると (x2-x1)/dt=v2 の形になるので、x2の式にすると x2=v2dt+x1 になります。 運動方程式F=maのほうも差分化しますと dv/dt=-kx2/m が m(v2-v1)/dt=-kx2 になるので、v2の式にすると v2=-kx2dt/m+v1 になります。 下の図の時間刻み幅dt=0.1、質量m=1、比例係数k=1、初期速度v0=1、初期変位x0=1 として、 変位xと速度vにそれぞれ x=if(sw、vdt+x、初期値x0) v=if(sw、-kxdt/m+v、初期値v0) を意味する循環参照を施してやってdelボタン押しっぱなしとかで再計算し続けますと、 速度と変位がいつまでも往復する様子が描けると思います。 ちなみに、k=m=x0=v0=1にそろえて v-x(速度:縦軸、変位:横軸)をグラフにして、 先ほどの空気抵抗のとき同様、循環参照初期化スイッチ(sw)を一旦オフ(0)ってからオン(1)にしますと 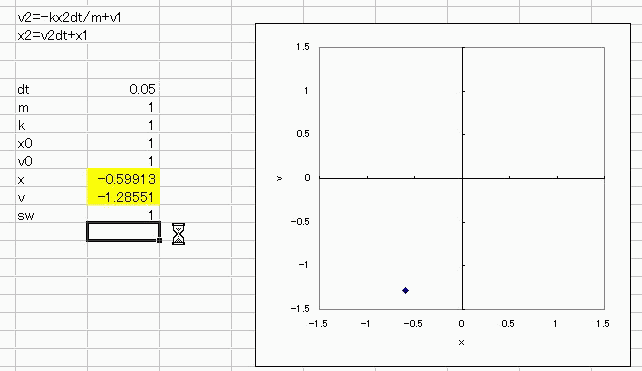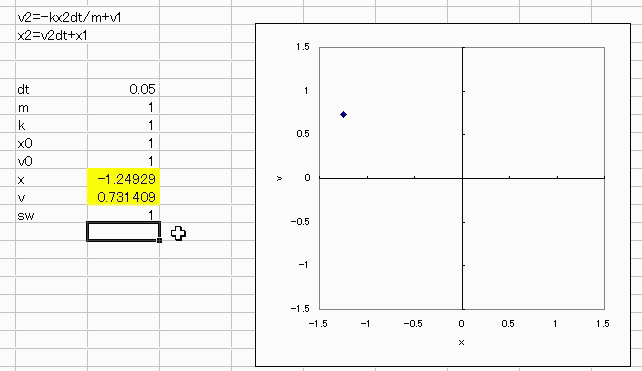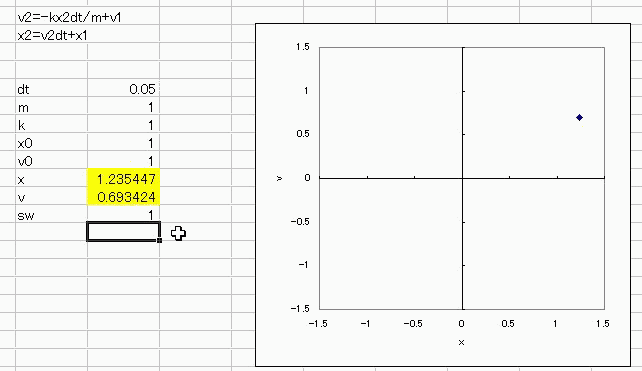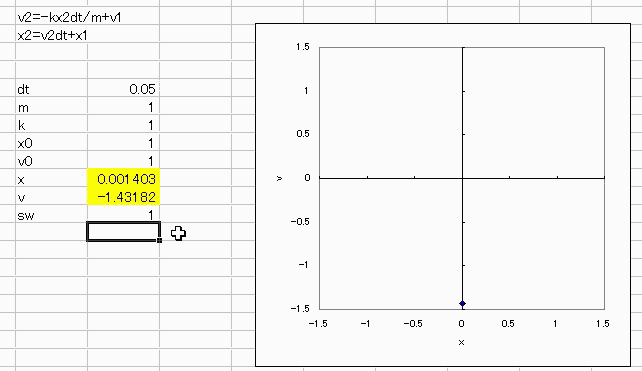 半径約 宇宙キターーー!!  にほんブログ村
ちょっと古い話
 おととしくらいに、コサインボルトのダジャレを具現化する方法を考えたんだ。 I(t)=Ic・cos(φ(t)-π/2) =Ic・cos(∫V(t)dt/Φ0-π/2) これの、I(t)に抵抗でもかましてRI=Vとかってしたらさ (V)=cos(V) フォッフォフォッフォフォー みたいなヘンな式ができそうじゃんか。 これをVについて解きたかったらどうするよ? V=√(V+1) とかだったらな、単に両辺2乗して2次方程式解けばいいだけの話だし cosV=a だとしても逆関数使ってV=Acos(a)ってすればそりゃぁ解けるけど cosV=Vは自分自身とイコールだからなぁ 2分法でも使って数値解析しないと解けないんじゃね? つうわけで循環参照の出番キマシタヨー ======= 方法 1つ目の表 F4:循環参照開始スイッチ(オン:1、オフ:0) F5:Vの上限初期値→1 F6:Vの下限初期値→0 2つ目の表 D列:V 上からそれぞれ上限、下限、中点 中点=average(上限、下限) E列:cosV→cos(D列) F列:2分法の判定符号。V-cosVの符号。sign(V-cos(V)) 循環参照部分 D9=IF(F4=0,F5,IF(F11=F9,D11,D9)):上限のsign=中点のsignなら中点のVを採用、≠ならV上限を維持 D10=IF(F4=0,F6,IF(F11=F10,D11,D10)):下限のsign=中点のsignなら中点のVを採用、≠ならV下限を維持 ※ただし、循環参照スイッチがオンのときに限る。 循環参照がオフのときは初期値(上限、下限それぞれF5とF6)を保つ。 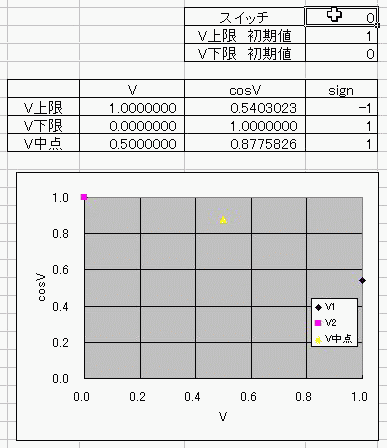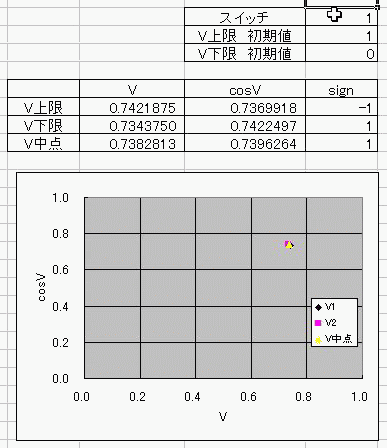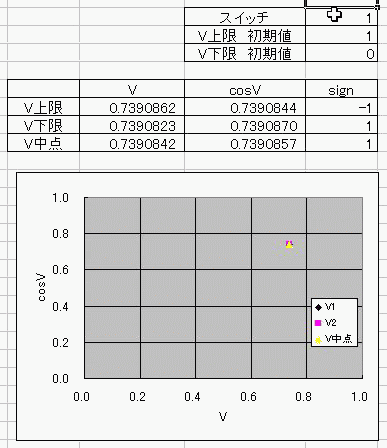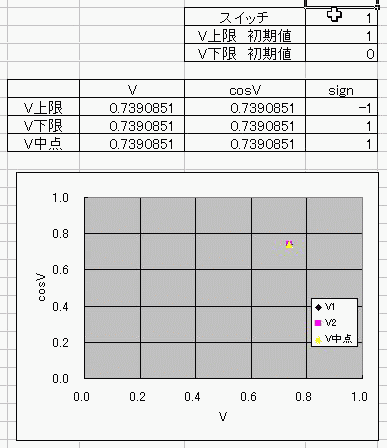 ====== だいたい0.74rad(42度くらい)でコサインボルトはボルトだそっすよw  にほんブログ村 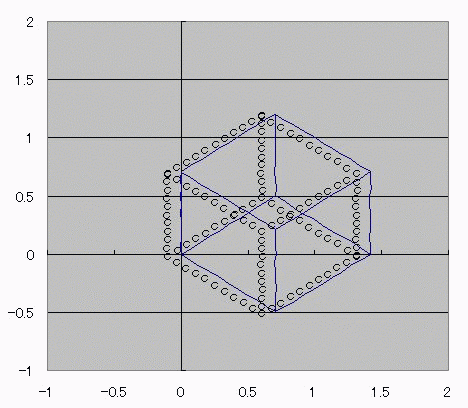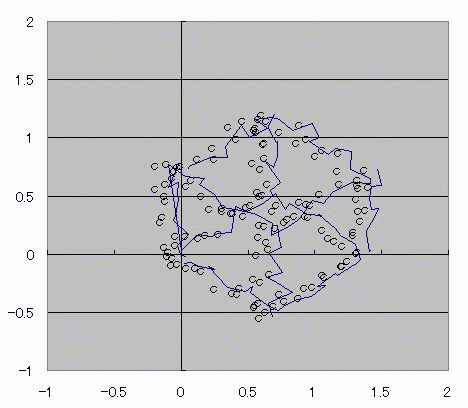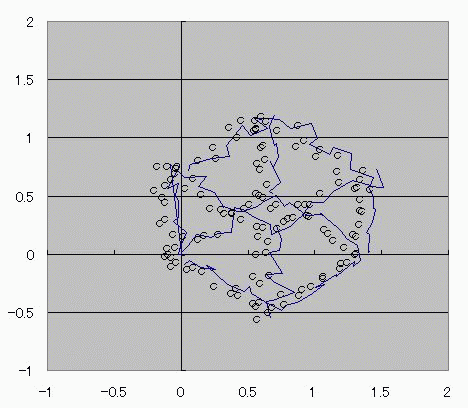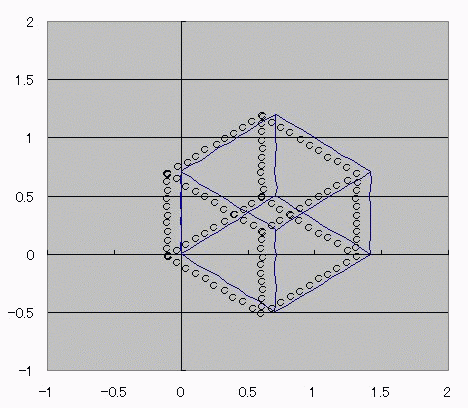 このアニメーションの作り方を使って、循環参照のイイトコロ宣伝を日記にしようと思ったんだけど なんかこう最近は妙に意欲が中途半端でね>< たぶんあれだ きばって書こうぜとか思ってるから1日おきとかになるんだ。 もっとこう、書きたいことを素直に書けばいいんだよな。ブログなんだし。 日記をきばって書くのからさぼって、現実逃避のためにまだやってない計算に手を出してみたりして 本末転倒のようなそうでもないような 昨日はガンマ関数の複素化に手を出してみたりしてた。 前に、4次元とか5次元とか、色んな次元空間における「球のようなもの」、「超球」って呼ばれるものなんだけど その超球の表面積と体積についてブログに書いたことがあって ガンマ関数の概念はそんときにwikiで見つけたんだよ。 階乗を整数から実数、複素数に拡張したものなんだけど それを使えば整数次元じゃない場合の球の表面積が出せるんだ。 実数次元ですらなくてもいい。 たとえば僕らのいるこの宇宙の万有引力の逆2乗則ってのが 実は精密に測ったら微妙に距離の2乗ではなくて2.1+0.1i乗に反比例してたとしたほうがつじつまがあうってなったら この宇宙の空間は実は3なんて整数の次元じゃないかもしれない。 そういうSSを書いたこともあった。 それをもっと具体的にリメイクするために、ガンマ関数の複素化が必要だったんだ。 でも複素積分とか周回積分とか、線積分とか 複素ガンマ関数に必要な周回積分のところでつまずいていたんだよずーっと。 で、季節も春になったしちょっと余力出してガンマ関数のwikiでも見直してみようか って見てみたら、周回積分回避できるっちゅうオチで・・・orz そんでまあ作ってみたんだよ相変わらずマクロなしで。 こんときのためにアドインしといたエクセルの複素数対応機能とか全然使わなかったし でもどういうわけか、精度がせいぜい有効数字1桁なんだよなぁー もっともっと繰り返しが必要なんだろうか・・・ っていうかここでこそ活かすべきなんだよな、循環参照。 そういやガンマ関数の計算方法見てたら オイラーの定数ってのがあんだよ! ネイピア数eとは別の! >超越数と予想されるが、無理数なのか有理数なのかすらはっきりしていない って!ちょー! まあ、超越数かどうかの判定だもんな・・・仕方ないな あれ?無理数かどうかの判定じゃんこれ。 やっぱおそろしいわー無理数。 π+eはどうも無理数ってことはわかってるらしいけど 超越数なのかどうかははっきりしてないらしいし。 超越数っていやぁ チャイティンの定数Ωって超越数を知ったのが3年くらい前だったか 定義もしっかり存在するのに計算不可能な数が存在するって。 雑誌で立ち読みしてたんだけど そんときは理解に苦しんだなぁー 理解できないっていうか、ホントに理解に苦しむ感じで、理解する気が起きなかったんだよ! あれだ、背徳的なかんじ! ヒマジン犯罪者に対して、その意欲をもっと別の方向に役立てろよって感じる一般人の心境! だってよ 2x+3=0のxを計算すんのに、次の問題で 「xって何回書きましたか?」 って言うんだぜ? しかも但し書きで「※xをaに置き換えたり脳内計算したりしてもムダなのよ!」 ってトドメまでさしやがって。 そんなチート問題解けるかーーー!っつーか解く気起きるかっつーの! 丸々3年は理解する気起きなかったし! でもそんなんにも欲張って手ぇ出す人がいるんだから数学ってのはわけわかんねえ世界だよな、うん そういやすっかり言い忘れたけど、いい忘れたからこそ追記。 オメガ数といえば、エロマエ・エロマエのアニメをパワポで作ったらメガバイト級で収まったりしないかとか考えてみたりしてw でもそういえば動画における音声と映像の容量比重はどうなってるんだろう? よく考えてみると動画の大半は音声でできています、みたいな感じなんだろうか。 確かに、gifとmp3を比べたらmp3のほうがでかいことなんてざらだもんなぁ じゃあ音声を全部ボカロにして、この人の声はこの音源、って感じにすればだいぶ圧縮できるんじゃないか。  にほんブログ村
ホームページやブログのアクセス数は、
「最初は全然人が入らないけど すっげー気長に待ってたら、ホントにすっげー気長なんですけど 待ってたら伸びたりするかもしれないんです」 昔見たアフィリエイト解説のページに、そんな感じのことがかかれてました。 でも、そんなにすっげー気長に待ってる間にホームページがブログに ブログがSNSやツイッターに・・・と需要自体が代わっていったら世話ないですよね>< というくらい、昔はその「一昔の長さ」自体がこんなに短くなっていくものだということすら予測がつかなかったと思うのです。 情報技術の進歩はそれだけ早いものなんだと思います。 実際、宇宙関連の技術も 光で見る宇宙技術と、人が実際に行く宇宙技術とでは雲泥の差ですよね その情報技術の進歩を支えているものといえばムーアの法則がありますが 1年半で同じ性能を持った部品が半分の大きさになっちゃうんです。 3年経てば4分の1ですよ これが、なかなかどうして さまざまな困難を乗り越えた結果として「1年半で2倍の性能」っていうのがなんとも不思議なところで あらかじめ困難を乗り切ることが運命付けられているかのような不気味さがあります これは何を意味するのかと考えてきましたが 去年の仮面ライダーオーズを見て 「もしかしたら欲望の力なのかもしれない」と思ってみたりしまして。 一番欲望が注がれる分野にムーアの法則みたいのが適用されるのではないかなと。 じゃあ、他にそんな分野はないのか? と考え、当時は見当たらなかったのです。 しかし、よく考えたら「数学」自体がムーア以上のペースで進歩しているのではないかと考えてみたりして。 数学は、他の分野への道具となります。 しかし道具として応用されるまでに数百年間、なんに使われるのかよくわからないまま眠っていることもあるそうで そういう状況が歴史上割と最初からそんな感じらしいのです。 これも、欲望のなせる業ではないでしょうか。 人間の3大欲求は怠惰欲・知識欲・省略欲、とはよくいいますが 数学者に変人が多いのは 数学以外の事柄に興味がないから、という話があります。 一般の方からすれば「かわいそう」にも見えますが 同様に数学者から見た一般の方もそういう風に見られているのかもしれません。 数学に夢中な人は、決して無欲なのではなく むしろ自分の興味の対象に誰よりも素直クーーーールに強欲で だからこそ、無償で人生をかけてまで考え抜いているのかもしれません。 そうでなくては、これまでに証明されてきた数々の定理が 幾重にも渡って不備を削がれてほぼ完成している と、あらゆる数学者からも満場一致で認められて 一般にも染み渡る、ということもなかったのではないでしょうか。 もし数学がそれほど魅力的なものではなく、確固としたものでもなければ 政治のようにいつまでもブレ続けて進展のないものになっていた んじゃないかなと思うのです。 それだけの欲望の対象にされているがゆえに 数学のジャンルだけが斜め上を突き進んでいて その進歩の加速度は情報技術のムーア則のはるか上を行っているのではないか と思えてきたのです。 そうすると、情報技術以外にもそういう並外れた進歩の例がある ということになるので、 何かの分野が、それだけ欲望を注げる対象になってしまえば 欲望の1番注がれる1分野に限らず色んな分野もこれまで以上に進歩させることができるのではないか と考えているのです。 ======= 最近、「数学ガール」という漫画で読んだ「ゲーデルの不完全性定理」も 80年以上経った現代において ようやくアニメに投影されるようになった そんな感じがします。 いわゆる「能力者バトル」というのがそれに当たると思います。 ストーリーでは、能力者同士が戦っている最中に、気分が高揚してなのか、お互いの能力の自己紹介を始めます。 最初は、相手の能力がわかっていながら太刀打ちできない そんな強敵に出くわしても 相手の能力そのものを弱点と捉え、倒していく そんなバトル要素を持った作品が時々あります。 ゲーデルの不完全性定理は、そういうところに応用(?)されて、一般認識されるようになってきている そんな印象がもたれます。 たとえば「もしもボックス(電話レンジ(仮))」能力などというチートすぎる能力があったとして もしもボックスの使い手と戦う(無)能力者は、ハロワのおじいちゃんの「長所は短所に変換可能だ」という名言を思い出し、なんとかして「もしも、もしもボックスがなかったら」という能力発動まで引っ張っていく そんな感じでしょうか。 すうがくまやノックオンザ因数分解ズドアなんかがあ(り)ふれる世界線に生きたいです、往復切符で。  にほんブログ村
循環参照で広がる、文字通り無限の可能性に期待ですね^^
差分化した微分方程式を循環参照で解いたり ニュートン法や二分法で解析的に解けない方程式の数値解を求めたり マクロでやらないエクセルの可能性がぐんと広がった気がしますw 今日は余力がないので、備忘録的に方法だけ書いておきますと まず ・循環参照スイッチとしてA1セルに0を入れておきます。1にするとスイッチオンです。 ・A2セルには初期値をぶち込んでおきます。 ・A3セルは、たとえば初期値からの総和を求めたいときなんかには if(A1=0,A2,A3+1)などとしておいて ・ツール→オプション→反復計算のチェックをオンにすれば delボタンかなんか押して再計算するたびに循環参照してくれるみたいです。 自由落下のアニメーションとか、弾道シミュレーションのアニメーションとか スーパーボールのアニメーションとか、ターミナルベロシティのアニメーションとか 振り子のアニメーションとか、波動のアニメーションとか なんかこう、夢が広がりんぐすぎて昨日は寝るのがちょっとだけ遅くなってしまいました^^; 使ってるセル数めっちゃ少ないのにアニメーションできちゃうってオメガ数的に考えて最高じゃないですかー! 「循環参照とは」のわかりやすい例えとして A「時間って何?」 B「時刻の連なり!」 A「じゃあ時刻って何?」 B「時間の一瞬!」 といった感じの、明瞭な表現を見つけました^^ ところで、エクセルの循環参照の例をぐぐって初めて気づいたのですが A「アンパサンドってなに?」 B「アンドがパサまったサンドイッチだよ!」 といった感じの、相互ではなく自分自身の循環参照が一番単純な循環参照だったことにうっかり気づいていませんでした><なんてこった! げえ  にほんブログ村  ウーウェ~ このコーナーではフーリエ変換っていうのがどういうものなのかをゴワッとだけご紹介しまっす fという関数があったとしますね 関数fの引数xがx=3のとき、f(3)と書くとしますと 図で描くとこうっすね、ハイカラな感じっす 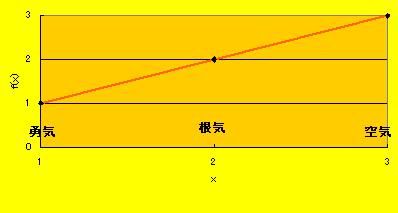 ところで fという同姓同名のベクトルもあったとしまっす 3次元のベクトルっす。 3つの軸の名前をそれぞれ1つ目:勇気、2つ目:根気、3つ目:空気と名づけるっす ベクトルfの空気:3つ目の軸成分はf3だから3っすよね 図で描くとこう、ハイカラなレーダーチャートになるっす 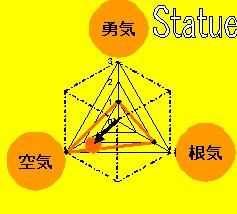 >そっとしておこう 実は、このf3とf(3)は同じものっす fなんて名前の同姓同名がこんなに近くにいたらたまったもんじゃないっす これがフーリエ変換のアイデアなんすよ じゃあf3(3)とかはどうすればいいかって? そんないっぺんにモテ期がこられても説明に困るっす。 自分不器用っすから、f3(n)のnについて勝手に積分して平均でも取ってくださいとしか言いようがないっす フェアリー テイラーな魔法展開はフーリエな1なる魔法展開に敵わないっす^^  にほんブログ村
不等式と背理法がすげー輝いて見えるテーマ。
だってよ 「相加平均(a+b)/2=log(√(AB))と相乗平均√(ab)の大小関係を述べよ」 っつって、多項式 (a+b)/2-√(ab) を素直に2乗して零判定してたら埒明かないわけよ それが (a+b)/2<√(ab) が成立すると仮定して両辺2乗してその仮定を全力でフラグクラッシュするんだぜ! そしたらかなりすんなり計算が終わる!スタイリッシュQED! めっちゃシビれるじゃん (a+b)^2<4ab a^2+2ab+b^2<4ab a^2-2ab+b^2<0 (a-b)^2<0ではない だから相加平均>=相乗平均←これだけだぜ?まじ素敵。 ※実数でやったら証明できましたカッー!   にほんブログ村  ええと・・・そうすっと金は増えるの!?減るの!? 2重以上の否定に人間はとことん弱いですよね。 まあ、約6万重<まんじゅう>の否定が偶数回だったか奇数回だったかってコンピュータが言われても有効数字3桁しか格納してなかったらそれはそれで苦手には違いないですし 鶏が先か卵が先かって言われて覚えてる生物もいないので 結局有限の宇宙だといかなる存在も多重否定は苦手なのかもしれません。 論理値<boolean>ったら上限も下限もあり、連続ではないしテンソルでも行列でもベクトルでも複素数でもなく無理数でも分数ですらない 単位元だけかもしれないし、零元もないかもしれない、零元の代わりにマイナスの単位元かもしれない たった1桁の2つしかない値なのに、それを複数回反転させるだけでなんでこんなにややこしいんでしょうね。 でももし、人間がいつまでもしぶとく生き残る可能性も皆無ではないわけで そうするとどうしようもないことを繰り返しているうちに数学だけは発展し続けたりして 有限の宇宙の中で時間だけが果てのない感じに映るのだとしたら、その有限の中で人類はどこまで 物理にはない「数学の無限」に迫れるのか・・・ やっぱり「宇宙を認識できる存在」が宇宙にいることは奇妙なことでありかつ、必然なのではないか そう思えてきたりします。 「宇宙を認識する存在がいない宇宙」というのは存在しているのかしていないのか 存在意義はあるのかないのか。 肉のない野菜炒め 「蛙を総合的に見ると尻尾はあるのかないのか、フロッグテイルの名の由来はそんなんだったかな」  にほんブログ村
だから、8を7で割ったら5なんだよ
9で割ったあまりの世界ではな! ほら、5×7=35は9で割ったら8あまるだろ? つまり、9で割ったあまりの世界では5×7=8なんだ。 あ?35を9で割ったら3あまり8だ? 割った結果なんか気にスンナ。今はあまりだけを見てろ。 じゃあ 5×7=8と、5×7=35の両辺を7で割ってみよう。 ほらな? 5=8÷7と、5=35÷7は同じだろ? 9で割ったあまりの世界ではな!! 割り切れないようで割り切れてる事実がこの胸の奥でまだうずいてるよ  にほんブログ村
電気回路のは
LQ''+RQ'+AQ=V (※電荷Qの時間微分Q'は電流I、A=1/C、Cはコンデンサの容量 L:インダクタンス、R:抵抗、V:電圧) 機械回路?のは mx''+rx'+kx=f (※m:質量、r:速度に比例した機械的抵抗、k:ばね定数、f:力、x:変移) で、思ったんだけど 電気回路のLを加えた回路って面倒くさいけど 機械回路でmを取り除いた計算も面倒だよな 電気回路だと基本、Lを除いてRC回路で代用したがるけど 機械回路だと逆に、基本的にはmkとかmr回路になるんだよなー や、ちょっとな。 めっちゃ基礎なんだろうけど 体重計の直列・並列のことを考えててな まあ重力質量と慣性質量を同じと考えて、ばねばかりで測るとするわけよ もちろん、そのばねの変移xは自然長さからの伸びで考えるし 理想的なフックの法則でしか考えないからめっちゃ簡単な計算なんだけど 100kgの魚人を4つの体重計で並列に量ったら体重計1つあたり25kgって計測されるわけじゃんか でも体重計Aの上に体重計B 体重計Bの上に体重計C 体重計Cの上に体重計D 体重計Dの上に人魚さんが乗っかるようなことをして 全部の体重計が100kgで表示されるんだろ? 何の利益もなくデメリットしかないように見えるのはなんだろう? たとえばそのばねばかりが75kgまで測れるものだったら並列にしたらメリットじゃんか でも、体重計直列で何の利益があるよ? よくわかんないんだよなぁ なんか引っかかる・・・ これがよ 機械的ばねを電気的コンデンサに相当させたら 同じ容量のコンデンサ2つ直列だったら1つあたり同じだけ分極するわけじゃんか いいかえると電荷や電流を共有してるわけだ それに対して並列だったら電圧を共有する。 ばねだったら並列だと変移を共有する じゃあ直列だったら何を共有するんだ? 電荷Q→変移x、電流I→速度v、電圧V→力fのアナロジーで考えたら力を共有するのかな? で、今更ながら気づいたんだけど コンデンサの容量Cって LQ''+RQ'+AQ=V をA=1/C使って書き直すと LQ''+RQ'+Q/C=V になってCが分母にくるけど ばね定数kって mx''+rx'+kx=f あくまで分子にきてるんだよなー それでいて直列の合成ばね定数がコンデンサ直列の合成容1/C=1/C1+1/C2みたいに 1/k=1/k1+1/k2の和分の積(逆数同士の足し算)で 並列の合成ばね定数がk=k1+k2の単純な足し算になるっていうのはどゆこと? コンデンサの容量がインダクタンスとか抵抗の逆数的な感じになるのは コイルとか抵抗の場合は抵抗率みたいのに長さをかけて面積で割る のに対してコンデンサの場合だけ誘電率に面積をかけて長さで割るからってのはわかるんだけど ばね定数のほうがよくわかんないんだよなー っていうか、よくわかってなかったのがわかった、みたいな。 そもそもばねがどうやってできてるのかよく知らない もしかして、機械の力学モデルそのものの直列と並列の概念が 電気回路の直列・並列の概念とそっくり逆になってるとかなのかな? 力学:直列←→電気:並列 力学:並列←→電気:直列 みたいな? 質量や空気抵抗の直並列・・・?ん? あとあれだ クーロン力で引っ張られるときの加速度が自身の電荷に比例するのに 万有引力で引っ張られるときの加速度が自身の質量に関係ない いわゆる「1tのはねと1gの鉄を真空で落としたら同時に地面に落ちる」話 ってのが体重計の直列に影響するのかしないのか(しないような気がするけど) ちょっと今は疲れてるから備忘録的に書いておいて あとで余裕が出たら計算してみよう。 ゴムの伸縮はエントロピー的で、エネルギー的な伸縮のバネとはメカニズムが違うんだってさ。 まあなんだ、お金がエネルギー的じゃなくてエントロピー的だから保存はしないわ 回すだけで価値が増えるわで、 エネルギーで考えたらなんだか永久機関みたいで気持ち悪い!ってなそんな感じだわな  にほんブログ村
今ようやく気がついた・・・orz平成24年で西暦2012年の今年の今日、2月15日に。
まあ昭和生まれ、平成育ちの人は昭和と平成の下2桁について考えたくもなるよね 対象・明示生まれ、昭和育ちの人だと大正、明治、昭和と西暦の下2桁を比べるんだろうけど そこんとこ世代がズレると共通認識がなかなかないもんだよね。 じいちゃんが何気なく「大正が西暦何年だから云々」って言っても孫には全然ピンとこないよな。 12年ずれているってことは、当然西暦が偶数だったら平成も奇数じゃないし 12は約数も多いから、 3や4や6で割ったあまり同士も西暦と平成では一致するはず。 やってみよう。
ところで、少林ナントカが流行った年の小学校で小林さんがショウリンさんって呼ばれるのと同じくらい 修学旅行で東北を訪れる際の小中光年の人の間では中村さんがジェイソン寺って呼ばれるんだろうなぁ ======= あの・・・テラジェイソンくん・・・渡したいものがあるの! え!?いいのかいテラ少林さん!こんな手作り感満載の・・・!じゃあ来月の円周率の日には必ず肉まんをご馳走するよ! あ・・・その・・・14日はやめよう・・・?昨日はチェンソー日の金曜日だったし今年は平年だから来月も同じ曜日になっちゃうよ・・・そろそろお互いこのあだ名も卒業したいし・・・ じゃ、じゃあどうしよう・・・? 7月の22日なんてどうかな? ああ!夏の円周率の日だね!じゃあキミの肉まんを拝みに行ってもいいかな^^ そ、それはいいよ・・・ 決行だね!ありがとう!じゃあ夏にまた会おう! こ、こちらこそ〃∇〃  にほんブログ村  α粒子Q「俺たちはどこですれ違ってしまったんだろう・・・」 α粒子A「偏角にして45度あたり、かな」ベーシ!ベーシ!ノシ  Q「ずいぶん具体的なんだな・・・」 ガイガーカウンター「測定の結果、両者引き分けです!」 Q&AΩΩΩ「ど、どないやねーん!?」 Q「クッ・・・俺だ!機関がまた俺をハメようとしているッ・・・!L・ψ・コングルゥー・・・ジョンッ!」 A「なにそれ顔みたいwィョゥL・ψ・¬シュタッ!俺3乗インザゲートってか?ww」  にほんブログ村 服<シュタインズゲート>の選択を間違えた。洗い終わらなかったんだよ・・・着て行く服がない・・・ |
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





