クォータニオンでジャイロの味噌擂りみたいなのを表現してみましたbyエクセル

なんとか、クォータニオンによる回転の、1つの点の処理を1行に収めることができました～

前半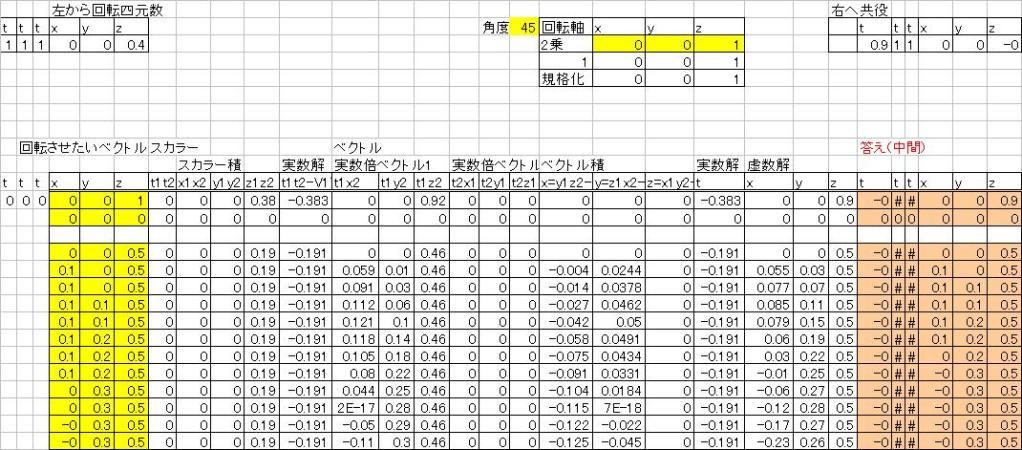



後半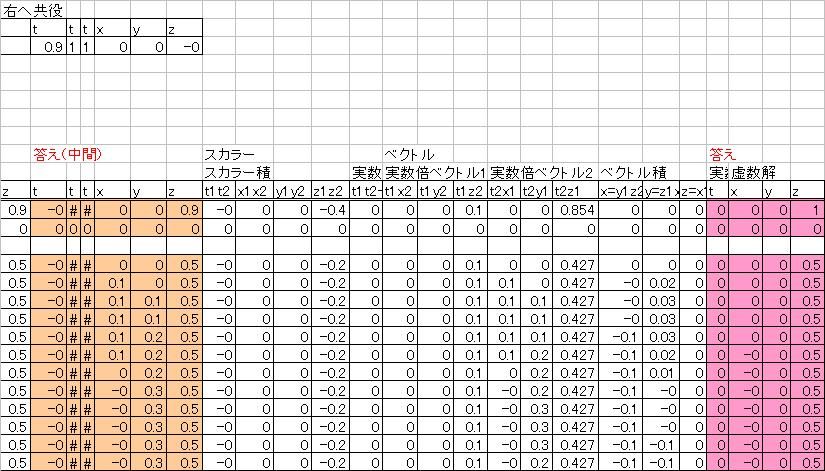



全然コンパクトじゃないですね、はい。
それもこれも僕のバグ発見能力の皆無さゆえにプログラムが組めず、エクセルで処理しているのが原因ですorz
四元数のみなさんすみましぇーんTAT


このエクセルファイルでは
多数の点を、1つの回転ルールに従って回転させることが出来ます。
下側の表の1行が1つの点に対応します。

上の表は回転のためのクォータニオン「左からかけるやつ(図1)」と「右からかけるやつ(図2)」と
回転軸・角度設定の表です。

回転のルールは1つのシートに1つといった風にしか押し込めなかったので
順次シートを替えて次の回転の指示をさせます。
(sheet1のピンク色の結果をsheet2の黄色の入力欄に代入する感じ）


クォータニオン(四元数)はx,y,zの3次元の点の位置を3つの虚数単位i、j、kを用いて表現し
付随する情報を実数tを用いて表現します。
その場合、1つの点はクォータニオンAを用いて
A(t;x,y,z)=t+ix+jy+kz
などと表現します。
3次元空間を扱うので、実数部分tは通常ゼロです。


A1(t1;x1,y1,z1)とA2(t2;x2,y2,z2)を掛け算する場合は
複素数的に多項式として展開しても構いませんし

(t1+ix1+jy1+kz1)(t2+ix2+jy2+kz2)

(i^2=j^2=k^2=-1や、ij=-ji=k、jk=-kj=i、ki=-ik=jを使って項をまとめます)

A1A2(t1t2-V1・V2;t1V2+t2V1+V1×V2)

という公式(というか解釈)も存在します。
(たぶん複素数との相性が悪い)エクセルファイルではこちらを用いて計算しています。
符号や添字が対称的なので覚えやすいですね！

Vは空間x,y,zをまとめて表現したもので
実数部分(セミコロンの左)と純虚数部分(セミコロンの右)にある・と×はそれぞれ
内積(スカラー積)と外積(ベクトル積)です。


クォータニオンで表現した3次元のベクトルAを回転させるためには

回転軸のベクトルを(0;a,b,c)であらわし
(ただし、長さは規格化しておく：a^2+b^2+c^2=1)

回転角度をθとすると

ベクトルAに左から

p(cos(θ/2);asin(θ/2),bsin(θ/2),csin(θ/2))

をかけ、さらに右からpの複素共役

q(cos(θ/2);-asin(θ/2),-bsin(θ/2),-csin(θ/2))

をかければ回転が表現されます。

pAqです。四元数では掛け算の交換法則が一般に成り立ちませんので、順番に注意してください。

p1であらわした回転のあとにp2であらわす回転を行いたい場合は

p2p1Aq1q2
といった感じで両側にどんどん追加していってOKです。


回転行列と違って任意の軸での回転ができます。
また、ジンバルロックがないのも魅力です。シンバルではないですジンバルですよ。


そんなこんなで出来上がったのがこれ。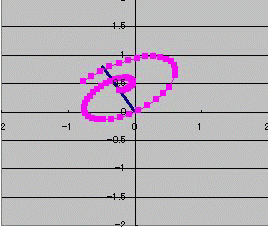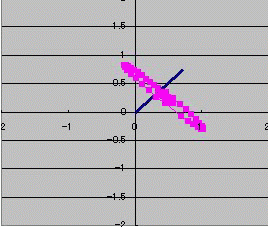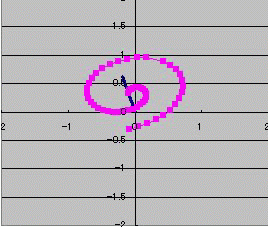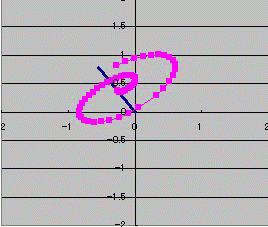


ジャイロっぽいのが味噌擂り運動してるっぽいgif動画です。
方針としては
１．xy平面でコマを回し(1シート目)
２．y軸を中心に45度回転させ(2シート目)
３．z軸を中心に１．の1/5の速度で回転(歳差運動：3シート目)
４．簡単な1点透視型遠近描写(奥行きyに比例してxとzを小さくする)



とりあえず最初のなんでこんな出来です。
今後もっと複雑なものを表現してみたいですねえ。飽きてなければね･･･。

今回はnow()-today()に100万くらいをかけた式を使ってミリ秒を取得しdel押しっぱでヌルヌル再計算で動かしていましたが
循環参照でも同様のヌルヌルができそうですね。
少ないセル数で色々できるのはいいのですが、可視化が悪くなるのがちょっとまだ慣れません＞＜

循環参照と100万なう－きょう関数は相性が悪いのでどちらか一方を一貫して使う必要がありそうです。



ところで自分、パウリ行列のwikiを読んでたらクォータニオンに漂着したんすけど・・・関係性がわかりません＞＜

にほんブログ村

放送大学って15回目が最終回なんですね･･･

14回目の量子力学の授業の最後に「パウリ行列が出そう」ってワイワイしてましたがそんなことはありませんでしたorz

最終回の15回目は先生が交代し、かなりの駆け足で素粒子論をかっさらっていきましたー･･･
あー、だから授業のタイトルが「量子力学」ではなく「量子物理」なんですね･･･
扱う素粒子の種類がめっちゃカラフルっす＞＜まぶしいっす･･･SRS48っす



素粒子論は･･･僕が高校に入って最初に手にしたつもりの量子力学の本に書いてありました･･･
中学のころに見たSFアニメで量子力学の勉強に憧れてた僕は、その講談社ブルーバックス「10歳からのクォーク入門」とかそんな感じの本を読み進むうち、「ナンカコレジャナイ」感をひしひしと感じていくのでした･･･

そして次に読み始めた講談社ブルーバックス「量子力学の語る世界像」あたりの本で
量子力学の無味無臭感に軽く打ちのめされそうになりました･･･
電子しか出てこない･･･




まあそれはさておき、今回の15回目はかーなーりーガッカリしましたが、
それでも10月からの2学期からまた放送される、おそらくまったく同じ内容の「量子物理」の録画を決意する管理人でありました･･･。



放送大学は1年を3分割して15週ひとまとまりにするらしく
春に始まってGWには休んで15週
次に1.5学期めいたものが入って
10月から2学期が始まって年末年始を休んで15週
といったサイクルになっているようです。


今日明日あたりから10月までは、1.5学期とでもいいましょうか
集中講義期間というものらしく
毎週ではなく毎日、講義がぶっ続けで行われるみたいです。
予約しました＾＾



やーこの授業形態はいいっすよ！
生の人間による授業なのでサイトを読むよりも受動的に頭に入ってきますし
テレビなので基本的に料金かからないですし
録画できれば「生の授業みたいに聞き逃したらはいそれまで」ってこともないですし
いいとこどりしてますよ、うん！
まあ今回の量子力学で痛感したのは「そんなに詳しくもない」ってことですが、
それでもNHKよりは詳しいと思います。
放送大学＞NHK＞ほか　な認識。



次の日記あたりで、パウリ行列の導出をやってみたいと思います。



ぎゃふん

にほんブログ村

クォータニオン(四元数)

四元数はこうやって記述するんだってさ☆

A(t;x,y,z)=A(t;V)

A1(t1;V1)とA2(t2;V2)の積
A1A2は
A1A2(t1t2-V1・V2;t1V2+t2V1+V1×V2)

になるんだってさ☆まじすか



あるベクトルA(0;x,y,z)を
ベクトルB(0;x0,y0,z0)を軸に角度2θだけ回転させたい場合は
ベクトルBの長さを1に調整して
（x0^2+y0^2+z0^2=1だと仮定して）

p(cosθ;+x0sinθ,+y0sinθ,+z0sinθ)
とその複素共役
q(cosθ;-x0sinθ,-y0sinθ,-z0sinθ)

を用意して

pAqを計算すれば回転するんだってさ！☆まじすか

回転のためのクォータニオンを複数用意して
p1、p2･･･って定めると
p1,p2,･･･A･･･,q2,q1
ってやれば次々回転してくれるんだってさ！☆




まあ確かに･･･ジンバルロックがないのは非常に喜ばしいことだけどもー･･･
慣れてないせいなのか、回転行列に比べて全然コンパクトになった気がしません＞＜


あーでもこれで棒の味噌擂り運動とか箱の味噌擂り運動とか表現したら楽しいだろうなぁー´pAq｀
もちろんエクセル(マクロなし)でやるつもりですｗｗｗ→いちおう雛形っぽいのはできました

回転軸を任意に設定できる影響は大きいですよね。



それにしてもクォータニオン･･･元々は
a+ibのaとbをそれぞれa=c+jd、b=e+kfみたいな感じで拡張したﾄﾝﾃｨのようなものだと認識していましたが
3Dの回転のことともなればずいぶんと記述方法が豹変したものですね･･･

a0+ia1+ja2+ka3
って4つの元としてのanがあって
虚数単位みたいのが3つ、ijkってあって
ij=-ji=k　ライター・マッチ厳禁
jk=-kj=i　タイマー・ラッチ厳禁
ki=-ik=j　マイラー・タッチ厳禁
って設定なんですよね。元々は。

今のソフト面の進歩速度というかドニョクサーはおそろしいものですよ･･･
20年ほど前まで禁忌とまでされてたものが積極的に活用されてるらしいですからね


ところで、この四元数のうち唯一ゆい５つの実数部分は
相対論の4次元に役立ったりするもんなんでしょうか
3Dでは基本的に使われてない領域ですよね。
なんか、実数以外の部分が全部何らかの虚部ってところが

時間はあなたがた空間とは違うのです
　　　　　　　 　　　　　　　　　　　　　　　　　　　,r;;;;ﾐﾐﾐﾐﾐﾐヽ,,_
　　　　　　　　　　　　　　　　　　　　　　　　　,i':r"　　　　＋ `ﾐ;;,
　　　　　　 __,､　　　　　　　 　　　≡　　　　　彡　　　　　　　 ﾐ;;;i
　　　　〃ﾆ;;::`lヽ,,_　　　　　　　　　　　≡　　彡　,,,,,、　,,,,､､　ﾐ;;;!
　　 　〈 (lll!! ﾃ-;;;;ﾞfn　　　　__,,--､_　　..　　 ,ゞi"￣ ﾌ‐!￣~~|-ゞ,　≡
　　　／ヽ-〃;;;;;;;llllll7,,__／"　　＼三=ー"."ヾi `ー‐'､ ,ゝ--､' 〉;r'　　≡　　世界線を客観的に見ることができるんです
　　　>､/:::/＜;;;lllメ　　　＼ヾ、　　ヽTf=ヽ　 `,|　 / "ii" ヽ　　|ﾉ
　　j,,　ヾて）r=- | ヾ:　　 :ヽ;;: 　　　 | l |　 l　 ''t　←―→ ）/ｲ^　　　　≡　運命探知の魔眼です
　,ｲ　ヽ二)l(_,＞"　l|　　　 ::＼;:: 　　　| |　 |　　ヽ,,-‐、i'　　／ V
　i、ヽ--ｲll"/　,, ,//,,　　　　:;;　　　l //　 l く> /::l"'i::lll1-=::::￣＼
　ヾ＝=:"::^::;;:::／;;;;;;;;;:::::::::::::: :::::ゞ ﾉ/　　 L／〈:::t_ｲ::/ll|─-=＝　ヾ
　　＼__::::::::／::::::::::::＿;;;;;;;;;;;;;;;;;ノノ　　　ﾍ　　　>(ﾞ ）l:::l-┴ヾ、ヽ　 ）
　　　　 ￣~~￣￣／　:::|T==--:::::　 ／／　　/　ﾄ=-|:|-─ （ l　　 /
　　　　　　　　 ／　::　 ::l l::::::::::::::::::/ /:::::::::::/:::::(ヽ--─　 /　|　 /
　　　　　　　　 ヽ＿=--"⌒￣ﾞﾞヾ:/ /:::::::／:::::::::`<==--　ﾉ　/　/

みたいなスタンスなのがハマりすぎて怖いというか･･･や、習いたてなんでわかんないですけどね
あくまで印象論（？）っすよ




日本の花火を上から見る

にほんブログ村

パウリ行列まじパネェ･･･

シュレディンガー方程式を使って水素原子様の波動関数を解いていたら
いつの間にか微分がめんどくさくなって代数に置き換えてみて
行列表記したらなぜかうまくいきそうで

代数の定義から許容される状態がなんかあるんだけどこれ物理的(波動関数)にあらわせないよ？ナニコレ？
(半整数の出番が与えられました：禁止されていないものは存在しなければならない)

→実はスピンという物理的実体でしたー。＾＾

スピンっちゅうのはなんかうまく表現できないけど
なぜか現象を再現できるからまあいいや。


スピンを考慮するとフントの規則がパウリの排他律としてうまく表せる。
ここでようやく、パウリ行列とパウリの排他律が同一人物からの産物だと認識がつながった。


スピンという量はどうやってもなぜか抽象的にしか表現できないらしい･･･まじかよ･･･



パウリ行列ってのはこんなやつなんだってさ。

なんてモン考え付きやがったんすか･･･

行列が単位ベクトルを表すなんて･･･しかも2行2列の複素数で3次元をあらわすってなんなの。
どういう発想なの？
あんたらには背徳感というものがないのですかっ！


パウリ行列を5行5列で簡潔に表すと
・2行2列の行列で
・固有値が全部±1の実数
・トレースがゼロで行列式がマイナス1
・エルミート行列であり、ユニタリ行列でもある。
・パウリ行列の積には次のような関係が有る
σi・σj=δij・σ0+虚数単位・εijk・σk　(ijk：１，２，３)
・(固有ベクトルが何を意味するのかは紙一重でさっぱりわからない)
反交換関係ってなんぞ･･･


ええー･･･
δijが「クロネッカーのデルタ」って呼ばれてるのはあとから知りましたが･･･これって単位ステップ関数ヘヴィサイドの階段関数を微分した「デルタ関数δ(x)」とすごく似てません！？
δijのi=jがδ(x-x0)のx=x0に相当する、みたいな。

εijkは「エディントンのイプシロン」っちゅう名前があるんすか･･･初めて見ました。
順方向だと1、逆方向だと-1、それ以外だとゼロですかー･･･


って、ちょっと待ってくださいよ！？
このイプシロンとデルタって、極限を論じるεδ論法ってやつと関連あるんじゃないんですか！？

自分、εδ論法習ってないみたいなんで、wiki見てもよくわからなかったんですけど･･･文字だけだとパッと見キツいわー

↓

もうちょっと調べてみたら、f(x0)→aになる極限の変数aに当たる微小量がδで、関数値fに当たる微小量がεらしい。
じゃあエディントンのεとはあんまり関係ないかもしんない。(・ω・｀)



･･･あれ？
同じものをかけたら単位になって
違う2つをかけたら残りの3つ目になって
掛け算を逆にしたら符号も逆になる･･･

あー
これモロに3次元の単位ベクトルじゃないすか･･･


でもそういえば行列同士の掛け算がスカラー積なのかベクトル積なのかよくわからんすな
どっちかっていうとベクトル積って印象すけど
じゃあスカラー積どこいったん？



やばい･･･これはやばい･･･
関連項目にクォータニオンがあるよ･･･
4行4列と2行2列が混在してるよ･･･どう理解すればいいのんじゃ･･･

あークォータニオン･･･こんなに便利だったのかー
これを使えばおっぱいや地球が簡単にたゆんたゆｒｎ
さて、複素数ですら相性の悪いエクセルに
マクロなしでどうやってスマートに四元数の演算体系を導入するか、そこが問題デスネ

にほんブログ村

フィボナッチ行列と、回転するのかしないのか行列の固有値・固有ベクトル

なぜだろう･･･ここからフィボナッチ数列の一般式までが遠い･･･＞＜



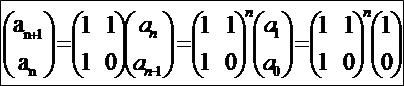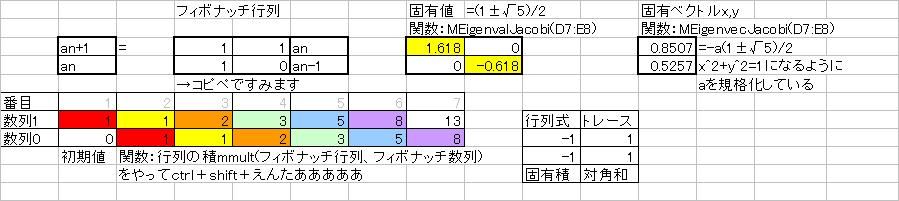n番目とn+1番目の比が黄金比に漸近するとこまではわかるのになぁ




ちなみにフリーのmatrixアドインを使って固有値・固有ベクトルを自動算出していますが
コイツ対称行列専用なので、回転行列の固有値出せないんですよねええええ･･･
せっかくオイラーの公式→｜exp(±iθ)｜=1→ユニタリなのにorz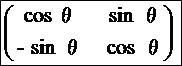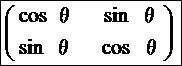



かといってこんな風に対称化した固有値λ=cosθ±sinθに何の意味があるんですかー

ってあるか。
コサインとサインにハイパボリックつければいいんですね。わかります。
λ=coshθ±sinhθ=exp(±θ)
エルミートになった代わりにユニタリ性を失ってしまいました！



実対称の代わりにエルミート共役にしてもなー
結局さっきの式と同じな上にこのアドインでは解けないしorz
(固有値は同じだけど固有ベクトルはさっきと違って±等倍じゃなく±i倍なんだな)

とはいえ行列で双曲線関数って･･･なんの意味があるんすかー
あ、でも僕は双曲線関数の何を知ってるというのですかー
そういえば定義しかしらねーや。


にほんブログ村

はエルミート行列だと言ったな？あれはウソだ！！
全体をiでくくってごらん？ほーら、たちまちエルミートじゃなくなるだろう？ﾅﾝﾁｬｯﾃ

水素原子ポテンシャルでの波動関数の節

オカリン「あれは昔、ギアナ高地でその辺の頁岩にぶら下がっていた力学教師に、どうして水素原子の電子殻は原子核に落ちないんですかとたずねたときのことだった。

べ、別に量子井戸だったら節が出来て存在確率が厳密にゼロになる箇所があることなんて知ってるんだからね！
そんなことを聞きたかったわけじゃないの！
どうして原子核の位置に必然的に節ができるのかを聞いているのよ！！！

見るからに穏やかそうなその力学教師「沢やかん」先生はいきなり豹変し、エルミート共役だとかルジャンドルだとかユニタリとかいう横文字めいた名前の概念を語り始めた。

5分で俺のキャパはあふれ、とりあえず
なんだか知らないが無限に落ち込むポテンシャルに電子は落ちない

的な結論を出しておいた。どうも存在確率がゼロの節がクーロンポテンシャルの中心に必ずくるらしい

あれから7年、31にもなっていまだにあえて厨二病全開の俺は、137億年弱前までタイムリープし、水素原子核に電子が捉えられる瞬間のねえどんな気持ち？を素っ直に聞いてみた。


電子の角運動量は量子化されその上ゼロ点振動しており止ることを知らない。
そのことで発生する遠心力的なポテンシャルがクーロンポテンシャルに重ねあわされた上で原子核の位置に必然的な節ができ、量子井戸になる。
そうすると節が生まれ･･･まるで卵と鶏のカモノハシごっこのようだ




にほんブログ村



3付近までの数をエコヒイキしているのは人間ではなく数自身なのか？

ただ純粋に数を数えることによって必然的に生まれる演算
加減・乗除・累乗と拡張していくと、いつの間にか交換法則や結合法則が成り立たなくなったりして自由が利かなくなる。
累乗を束ねた演算、たとえば2の2の2乗乗を2の3ナントカとかいう表現はまだ聞いたことがない。

次元の数も同様に、
どういうわけか2の3乗、8つの次元あたりまで拡張した複素数のようなものまでが限界みたいな感じを受ける
(2の整数乗以外の次元数はアウトオブ眼中な雰囲気で。)
8元数はかろうじて分配法則だけが成り立っているらしい。



数自身の構造を突き詰めると、果てのないタマネギかと思いきやどうやら3層構造が基本、のような感じがしてくる
追記：交換法則、結合法則、分配法則も3つでワンセットだし；


三角形が一番小さいn角形なのと関係があるかはわからないが
πやeなど割りと重要そうな無理数が3近辺にあるのは何か意味があるのだろうか。
(ただし、円周率を約6.28にするべきだったのではないかという疑問は残る)

まあ、多くとも10以内はエコヒイキ対象って感じだな。



ちなみに、半径1のn次元空間内での球(いわゆる超球)の体積は5次元、表面積は7次元付近で最大になる。
付近･･･か。
そういえばもっと細かく見てみたかったんだったな、次元数で微分したらゼロになるところを。
いや、解析的に求めたりなんかしないよメンドクサイ。
そんなんは数値計算でやるよ

5次元付近と7次元付近の間を取ったら2π≒6.28でしたとかいう流れだったら超ウケそう

ダイスーキカ

キャトられ系ラノベとかに出てくる「幾何学模様」っていうのがどんな模様なのかよくわかっていなかった。
なんとなくはわかるんだけど、じゃあ幾何学じゃない模様ってどんなのよ？
とか思っていた。
定義はわからないけど用法は暫定的にわかる、みたいな？
なるほど、簡単な図形だな？



同様に、代数ってどんなジャンル？
なんてことは考えたことさえなく
今朝考えた。
代数じゃない数学ってどんなジャンルよ？

微積分が代数のジャンルから少し外れるというのは初耳だった。



線形というのも結構奇妙なものだ。
だいたいはy=ax+bであれば線形だが、
狭い意味ではb=0つまり比例以外は全部線形ではないという場合もある。
世の中ほとんど非線形じゃねえか！
ただまあ、線形を重ねていった挙句に非線形を再現しようとする試みがあるから
線形がまったくの無意味ということもまったくない。




そんな今日の今朝は、量子力学の放送大学を録画して計算しながら見ていた。
ついに念願の行列力学に入ることができそうだ！
行列力学がわからないといい始めて10年くらい経つ。
微分方程式は一通り習った。数学の道具としての行列も習った。
固有値もだんだん理解してきている。
シュレディンガー方程式も解けるようになった。

しかし、どうも量子力学と行列が個人的にうまく結びつかない。
回路の解き方でたとえると回路方程式と伝達関数にそれぞれ相当するのはわかる。
しかし量子力学に具体的にどう結びつくのか･･･いや、思いっきり抽象的なんだろうけども。

だがそれも今朝でおさらばだ！
一方的な画面でのやりとりだろうと、やはり人間が生の肉声を使ってニヨニヨしながら解説してくれる授業はいい。
受動的極まりない性格の僕との相性は最高だ。
独学で教科書読むよりもかなりすんなり頭に入った。

来週の予想。
パウリ行列が出てくる。

だってスピンと昇降演算子が出てきたらあとはパウリ行列を待つだけじゃんか。
しかし「昇降演算子」でぐぐったときにwikipediaに昇降演算子の項目がなくて
代わりに似て非なる「生成・消滅演算子」が出てきてしまうのは問題だと思わないかい。

ただ待ってるのもつまらないのでパウリ行列を前もって導出しておいた。
エルミート性は確かめたが、パウリ行列のwikiを見るとそのほかの色んな性質ががら空きだ＞＜
ナニ！？ユニタリでもあるだと！？
固有値は求めたが固有ベクトルもトレースもデターミナントさえ求めていない。
詰めが甘すぎる。orz
つ、つかれてたんだよ！！１

ユニタリ行列の定義も見てみた。
やはり固有値(複素数)の絶対値の2乗が1になるような行列か。
回転行列の固有値はオイラーの公式なので回転行列はユニタリ。ですよねー！
｜exp(iθ)｜^2=1
行列に｜｜をつけたらまだ複素数だったのでさらに絶対値をつけてみたーみたいな。｜｜行列｜｜

わかりづらい前置きを書くんじゃない！読む気なくすだろうがー！
でもそういやエルミート性っていうのはどういう性質なんだっけ？
定量的に言えば複素共役を取って転置を取ったものが元の行列と一緒
これが定義っていうのはわかる。
じゃあ感覚的にこれが何を意味するのか。
ユニタリが極座標でエルミートが直交座標？？



しかしパウリ行列、いまだに不気味な存在として僕の前に立ちはだかる。
基本的に2行あるいは2列の行列に対するものなのに対象が3次元とはこれいかに。
3つ(あるいは4つ)のうち1つだけ虚数単位でくくれるっていうのも不気味だ。
4次元目はどこいってしもたん？

とにかく来週、水曜日の朝7時半、メイド喫茶「フェイリスニャンニャン」で放送するようになった量子力学の授業で
パウリ行列の不気味さが晴れるか見ものである。
健闘を祈る。L・ψ・ｺﾝｸﾞﾙｩ･･･


っていうか来週パウリ行列だよね？間違いないとは思うんだけど。
量子力学はHENTAIのすくつ。
量子力学でこの世を作ったやからも同様にHENTAI
しかしもっともHENTAIなのは、
なんに使われるのかもアウトオブ眼中で先に道具から作ってしまった数学者たちだ。
あれほどのHENTAI集団はそういない。
ちなみに全部褒めている。
猫は擬人化しない派。おっぱいだけは3次元派
にほんブログ村

しかし戸惑うのは男と同じくらいかそれ以下の貧乳になぜか最近魅力を感じつつある僕ガイルちゃん
　∧　∧
(*‘ω‘ *) 　
　(　　　)
　　v v 　　　
　　　　　　　　
　 　川
　( (　　) )

であることだ。





これ昨日アップしたつもりだったんすよ；ω；
満身創痍でアップしたから、前回非公開ジャーで登録したのが活きてたまま
それを自覚しないで公開ジャーしたつもりになってたんじゃよー；ω；ｼｸｼｸ
この悔しさを風化させないためにも、公開時刻は今日のままにしておくんじゃよー；ω；
Dメールで公開なんかしないんだからねっ
公開先に立たず･･･

かくし子コンビ ショートコント「中性的な粒子」

中性子「お前が男だったら俺はなんだ？」

陽子「そりゃお前は女だろ」

中性子「名前が中性的なのに俺ってどっちもじゃなくてどっちかだったんだ？」

陽子「電荷がプラス素電荷とゼロ素電荷の間が中性だからな。素電荷の半分が中性なんだよ。」

中性子「そうだったのか。えっ、3分の1じゃなくて半分か。あーだから俺たちって合体したままなのかー」

陽子「レゴであらわすとこんな感じ。俺から中間子を抜くと俺がお前になる」

中性子「いや違うだろ、俺がお前に中間子を挿すとお前が俺になるんだろ？」

中間子「もうどっちでもいいよ。どうでもいいから、俺を早くレンタルから解放してくれ」

陽子「いやそりゃぁムリだろ。もう出番出ちゃったしｆｋ(不確定性原理的に考えて)延滞エネルギー払えよ」

中間子「俺が払うの！？」

中性子「でもそういやよ、中間子が移動したら俺が陽子に、陽子が俺になるんだから俺たちの中の人ってもしかして中間子？」

中間子「あるあ、ねーよ。俺らメソンはバリオン数プラマイゼロだもん。ハドロン同士だからってお前らバリオンと一緒にスンナ。」

中性子「なんだ、バリオンの1/3はメソンでできています的な展開期待してたのに。」

陽子「あれ？じゃあメソンってクォークと反クォークでできてんの？」

中間子「だからお前らにナニが挿さろうがナニがヌけようがどっちでもいいってさっきから言ってんじゃん」


陽子「心底どうでもよかったのか･･･」

中間子「かなりガチでな」




ぐーるぐる

にほんブログ村

行列の固有値おもすれー

フィボナッチ数列の行列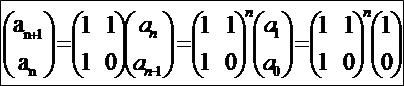とか回転行列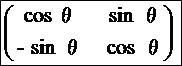とか、回転行列を対称行列に一部改変したやつとかの固有値・固有ベクトル見てみると別アングルから見てるみたいでおもしれー

絶対領域キャストオフで全裸待機的なｗｋｔｋ
いやそこはオフっちゃだめだろ

しかし今ようやく気づいたんだが･･･
エクセルに入れておいた行列アドインさん･･･固有値算出できると思ったら対称行列専用かよ！！orz
今朝知って朝からがっかりだったわ･･･
なんかおかしいと思ったら思わぬ落とし穴･･･
欝だしのぅ･･･

非対称行列に対応するためには有料アドインをご購入くださいって･･･アドイン公開してる人少なすぎだろ･･･
ヤコビ法みたくなんかアルゴリズムがあるなら自作しようかなぁ･･･
まあアドインはおろかマクロすら危うい知識だけど、循環参照を駆使すればできないこともない
かなーとも思う･･･。
せめて有限の複素平面にゼロ点界隈をグラフ表示ぐらいはできそうだよな。
なんか急にフリーのソース公開して需要がごっそり大移動･･･とかそんな夢みたいなことは考えたってできませんって。はい

そういやそもそもエクセル自体、複素数との相性があんまりよくなかったんだっけ･･･
いちおう公式アドインで複素拡張はできるっぽいけどiが文字扱いって時点で絶望がこいつのゴールでいいよねって思ったわ･･･
非対称だけど実数限定行列対応でも嫌だしなー
しかもその固有値実数とは限んねえし･･･


そういえば･･･重解出てきたら固有ベクトル同士の内積がゼロにならないんじゃないか･･･！？
あーそういや対角化とか習ったっけなー10年ほど前に。




n×n正方行列の固有値問題って基本的にn次方程式だけど
実対称行列とかエルミート行列の固有値の場合、ガロア理論とかアーベル群とかの解の公式みたいな条件集合に含まれるんだろうか？
そこんとこいまだに引っかかってるんだよねー

そういや、前に16次方程式の解の判別式のニュースのときに
∑(an・x^n+bn・y^n)=1
みたいな多項式っぽい円の方程式みたいなのはどんな形なんだろう？
ってのを考えてみた(だけ)ことがあったけど
Π(x-an)+Π(y-bn)=C
のほうがいいかもな。複素らないし。
簡単な具体例でいうと
(x-1)(x-2)+(y-3)(y-4)=1
のグラフの形とかどうなるんだろーみたいな。
平行移動に似てるけどどう違ってくるんだろう

にほんブログ村
はぁ具合が悪い日はなんか色々空想しちゃうよな暇だけに
明日仕事行けよ絶対行けよ

「実対称行列の固有値はすべて実数である」の証明

数年越しの重い腰あげてようやく読むことにした。

今日の俺はー気分がいいー(午前中だけだったけど)

こういうときは実際に式を書きながら追っていくと効率がいい。



ええと、ナニナニ？

「縦横n^2個の要素からなる正方行列Aの固有値λと固有ベクトルx(列ベクトル)は

Ax=λx

を満たすと定義される。」

そうだろう･･･？


Aが実数行列だと、Aの複素共役A~=Aであり
Aが対称行列だと、Aの転置行列A^t=Aである。
行列Aの転置と複素共役の両方を取ることをエルミート共役といい、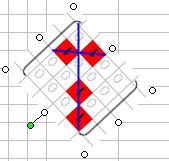A~^t=Aであらわす。
は「ダガー」と読む。
つまり、実対称行列であるAはエルミート共役に対して不変である。A=A^†
実はこれは実対称行列に限らない。エルミート共役に対して不変な行列をエルミート行列と呼ぶ。



固有値と固有ベクトルの定義式に対して両辺エルミート共役を取ると
x~^t・A=λ~・x~^t　　　ﾈｰ

である。この両辺に右から固有ベクトルをかけてやったもの

x~^t・A・x=λ~・x~^t・x　　　ｶｲﾊﾞｰ
と、固有値・固有ベクトルの定義式の両辺に左から固有ベクトルのエルミート共役をかけてやったもの

x~^t・A・x=x~^t・λ・x　　　ｶｲﾊﾞｰ

の左辺は同じなので、右辺を比べると

λ~=λ

となるので、λは全部実数でキマリである。


え、これだけ･･･！？まじで！？
数年越しにお気に入りあさったらあの「安定性になんとなーく定評のあるpdfファイル」すらリンク切れしていたから調べなおしたというのに･･･！

行列の要素にも要素数にも言及しないでスッパリ証明しやがった･･･！
なんだこれ！！こんなにアッサリだったのか！！！
もっと早く読んでおくんだったー･･･orz



ちなみに「固有ベクトル同士は直交をスルー(内積ゼロ)」
な、なんだってー！？

あ、ホントだ･･･具体的に要素ぶち込んだら全部直交しやがる･･･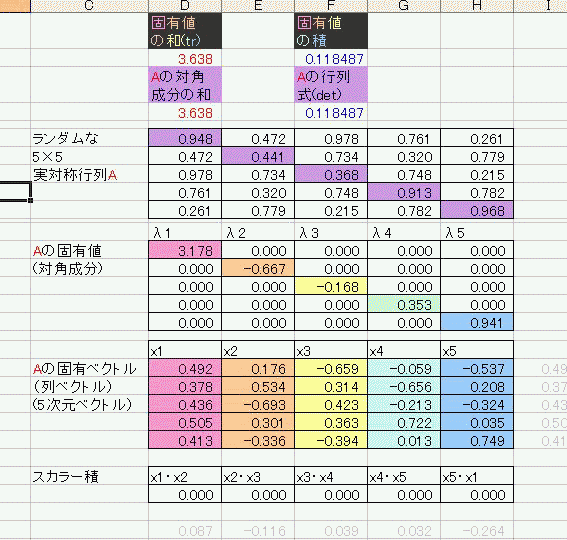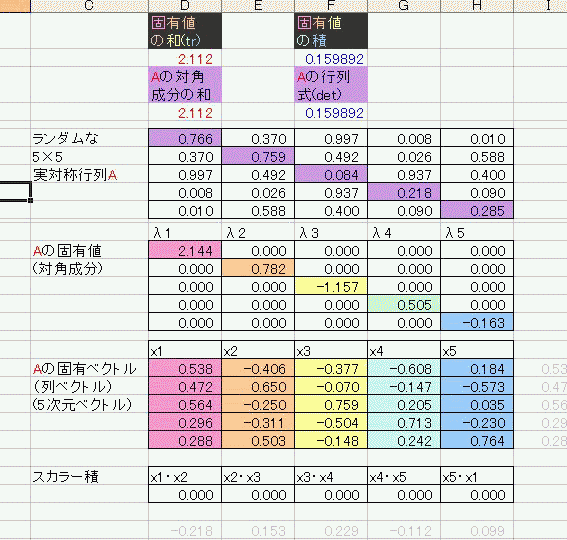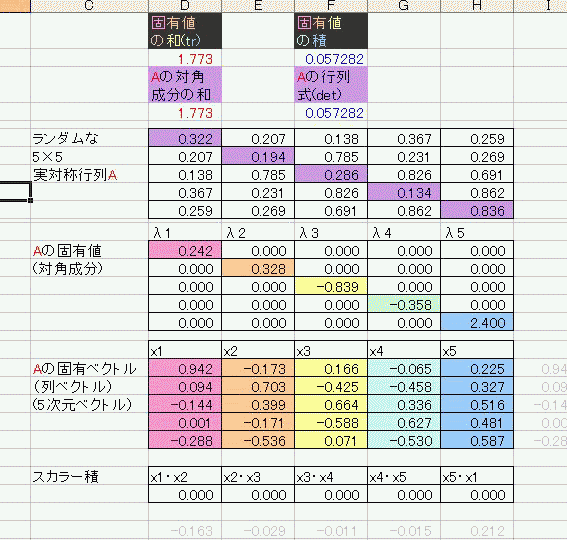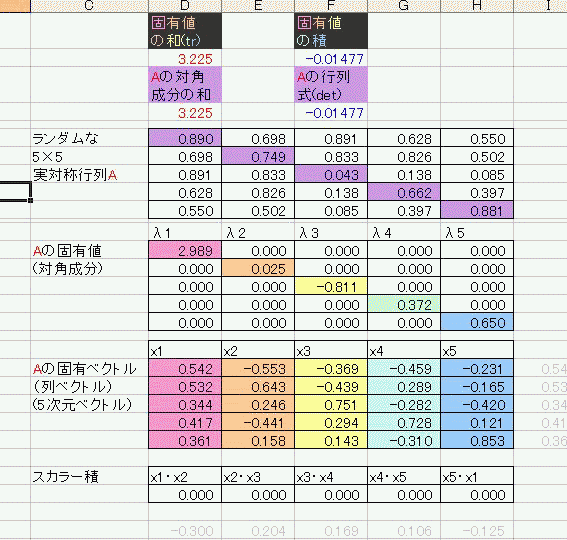
まじか･･･


にほんブログ村

マクロなしエクセルで実対称行列の固有値問題と高次方程式を解く！

n^2行列に見立てたセルに具体的な実数を入れておき
適当に見繕った固有値倍の単位ベクトルを引く
さらに、その行列式を計算し、


具体的な固有値を循環参照で変動させる。


算出した行列式がゼロを横切ればそこは固有値でしたってオチ。


何行何列の何次方程式になろうが(何は同一のものとする)
実数で対称な行列であれば固有値はすべて実数になるため
固有値を揺らす範囲は実数内でおｋという安全・安心・お手軽さ！
数値計算なので5次以上の解の公式云々は関係ない･･･！なんてこった！＞＜

循環参照は幅や高さ、奥行き(シート)に左右されないから、
2次元配列とも見なせる行列が相手だろうと劣化しない！

その上、時を司りる(×つかさどる○つかさドリル)女神であらせられる循環参照ベル・ダンディさんは
別に揮発性でもなんでもないんだからねっ
揮発か不揮発かすらコントロぉール可能なのだぁーフゥーッハッハッハ


ここまでマクロ一切なし。
マクロなしだって、固有値が解けるんだ！^{ﾊﾟ～ﾊﾟﾊﾟｯﾊﾟ～}
まあ、答え合わせにmatrixアドイン入れてたのは内緒。
で･･･デターミナントとトレースだけで答え合わせしたんだからねっ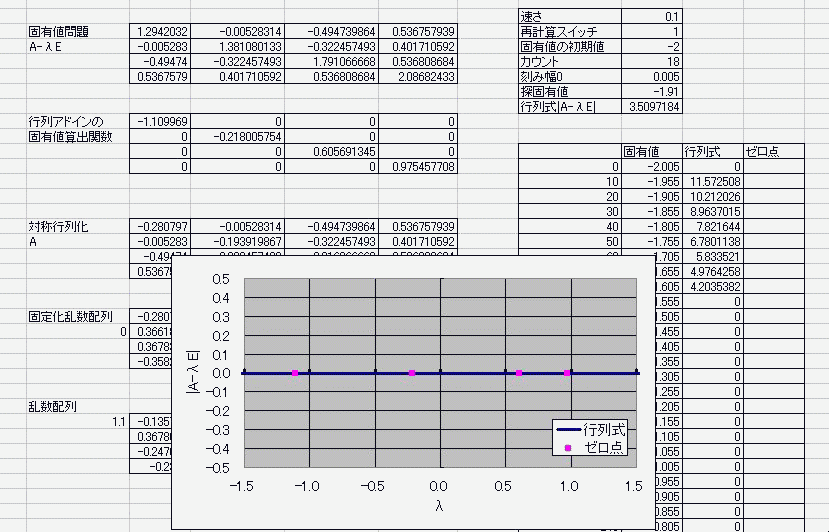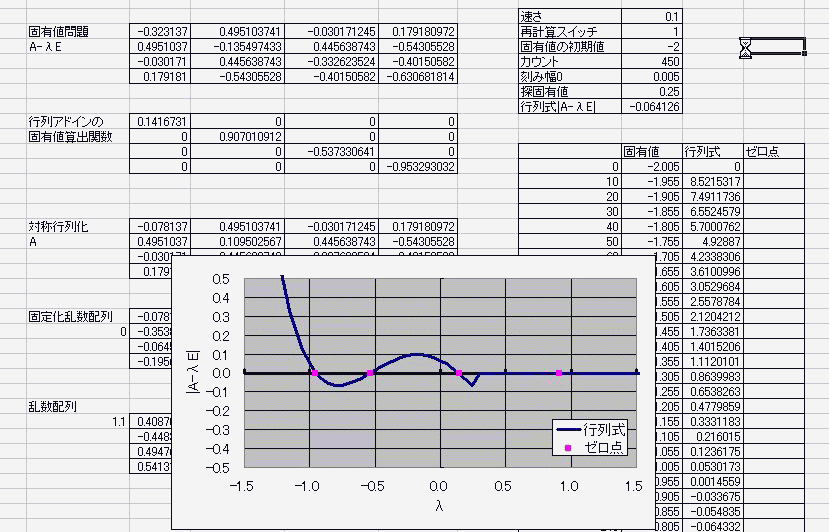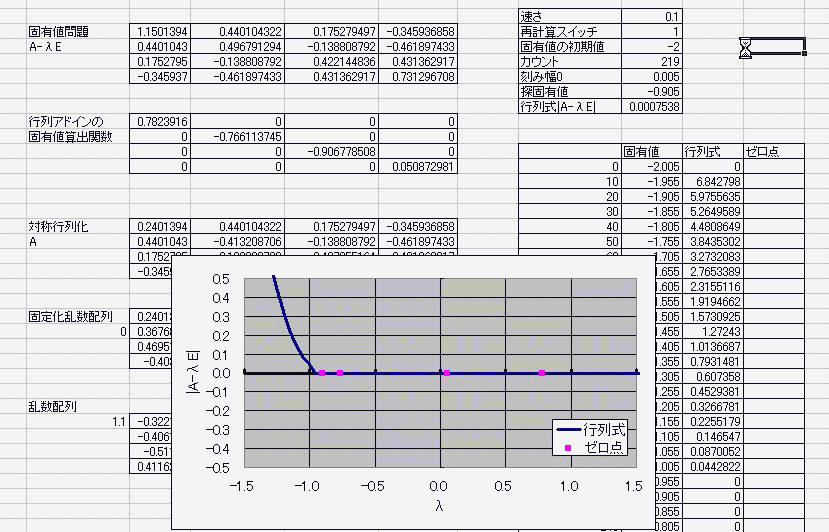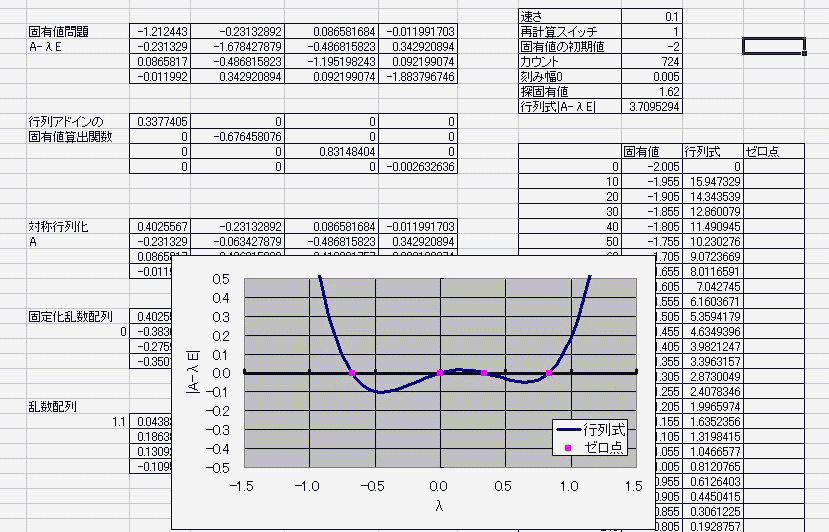



ただ･･･現状では(二分法使っておきながらも)精度がよくないのと
全自動とはいえないのと
重解のときの対処が人力であることなどが課題で･･･


そ、それと･･･エルミート行列の固有値が実数になる証明をまだ理解していなかったりしてー･･･

にほんブログ村

7の倍数の見分け方：1の位を2倍したものから10以上の位を右シフトして引く

たとえば154は7の倍数であるが

右端桁の4を2倍した8から、それ以外の15を引いてマイナス7
マイナス7は7の倍数なので、154も7の倍数である。


しかしながらこの方式では
154から2を引いた152に対して「5あまっている」という判定は出ず、
あくまで「7の倍数ではない」という判定結果しか出ない。

これでは非常にMOTTAI GA NAI


この「割り切れるか判定機(return：boolean)」を「あまり算出器(return：int)」に拡張するには
右端桁を2倍したものからそれ以外を引く
ではなく、
右端桁から、それ以外を半分にしたものを引く
にしなければならない。つまり全体を2で割るのだ。


154から2引いた152では
2から15を半分にした4を引いて-2=5となる。
2足りないのは5あまりと同じだ
7つの椅子を取り合う椅子取りゲームで人に対して5人あまっていたら、さらに2人足せば円卓は閉じて飲茶ができることと同じことだろう。



なぜ15を半分にして4なのか
15は7×2=14に1加えたものなので15=1である。

では1/2はどうやるのか
2倍して1になるものを探すわけだから、九九の2の段を逆引きして

×	0	1	2	3	4	5	6
2の段	0	2	4	6	1	3	5

4であることがわかるだろう。


もし、エクセルで(7で割った)あまり算出セルを作ろうと思ったならばアルゴリズムはこうだ。

目的の数がA1に入っているとすると(例：152)

右端桁以外を抽出するのにrounddown(A1/10,0)を行う。(152だったら15が取り出される)
(ただし、A1が負の場合も扱う場合はif(A1<0,roundup,rounddown)と演算することに注意)
これをB3セルに代入するとする。

それから右端桁を抽出するのに先ほどのB3セルを用いて
A1-B3*10
(例：152-15*10=2)
これをC3セルに入れよう。


そうすると、B3の右端桁と、C3のそれ以外桁から
D3=B3-C3/2
(例：2-15/2=2-1/2=2-4=-2=5)

で、本来ならばあまりが算出できるはずである。

が、答えであるD3が0～6に収まっているとは限らないので
収まるまで繰り返す。


といいたいところだが、C3が偶数であるとも限らない。

もし奇数だったら、上の九九表のようなことを行わなければならない。

ぶっちゃけていうと、あまりを出すMODという関数がエクセルには組み込まれている。

こいつは茶色文字で示したようなアルゴリズムで動く関数だ(と思う)

-5とかいう負の数もちゃんと2と翻訳してくれるし
(mod(-5,7)=2)

πで割ったらいくらあまるかなんてのもちゃっかり演算してくれる。(mod(5π/4,π))=π/4


しかし、小数(ほぼ無理数)で割ったあまりを計算してくれるからといって
整数であるmに対してmod(m/n,k)をきちんと算出してくれるとは限らない。

たとえば先ほどのようなmod(1/2,7)は0.5と出てしまい、4にはならない。

もし4のような結果を算出したければ
2にy=0～6をかけたものをx=2yとし、mod(x,7)=1になるまで演算を繰り返すようなアルゴリズムが必要だろう。
たとえば循環参照を利用するなど。


なぜmod関数の機能を実数にまで拡張しておきながら分数（：整数比）には拡張していないのか
おそらくだが、有限桁の実数をあくまで数値として扱うコンピュータとの相性が悪いのではないかと思う。
もしかしたら解析的に式を判断するツールだったら対応していてもいいのかもしれない。

エクセルではそこまで責任は負えませんよー的な感じで
やるならユーザの自己責任でドウゾな感じなのかもしれない。

上述のようにマクロを使わずにできないこともないし、それよりは実数に対応させるほうがよほど有意義なのだろう(たぶん分数対応(逆元探し)と実数対応は排他的)、まあ推測だけども。


フォーゼって2進数で書くと0地に1だっけ？1地に0だっけー？
え？限りなくシロに近いグレー？

にほんブログ村

TCD：0の0乗

あれ？前に日記で書かなかったっけ？ブログ内検索してもヒットしない。なんでだ？


それはそうと、何年か前に「0の0乗を極限からアプローチしていくと定まらない」
みたいなことを書いたような気がしていたんだけど
少なくとも考えてはいたはずなんだ。
ああ、あったあった。2010年4月21日の日記だ。



あ、そうか。この日はあくまで0のi乗について考えていたんだったな。
それにしても変だな。
wiki見たら「0の0乗が1っぽいけどそうでもない」って話にすぐ着きそうなのに
なんでそこんとこのこと考えてなかったんだろう？

aを正の実数に限定すれば
aをプラスから0にアプローチしたときだけ
a^aは1に漸近するはずなのになあ


F-ate∞/zero　このままだと来世からもハ_っサンですよ

にほんブログ村

MCD：量子力学的円グラフ

グラフの中で円グラフっていうのは僕にとってグラフの中ですごく異端なジャンルに見える。


グラフとして表記する数値が1種類しかなくても成立してしまうし
むしろ1種類しか許容してくれない

それに、上限と下限がある数値にはピッタリの、1周ぐるっと360度。
棒グラフだったら下限はさておいても上限(１００％)を引っ張りあげて改ざんすることが出来るのに対して
円グラフの場合は1周して元に戻るところは選びようがなく決まっている。
これは規格化にピッタリだ。

ただ、2πラジアン360度を１００％とするならば
その半分であるπラジアン180度やπ/2ラジアン90度を１００％とする半円＜ひとつなぎの2象限＞グラフや四半円扇形＜1象限＞グラフがあってもおかしくはないような気がしないでもない
3象限？ないな。



そこで、量子力学的なかんじで、ちょっと奇妙な円グラフを考えてみた。

1乗同士の合計ではなくあくまで2乗同士の合計が１００％になる円グラフ。
その名も、ユニタリーーーーー円グラフ！


しかしながら、
元々円になるようなグラフの横軸数値n個を2乗して合計してルートを取ってからnで割る平均
と
縦軸数値n個を2乗して合計してルートを取ってからnで割る平均
との関係は、残念ながら円にならない！＞＜

平均してからn個で平均取れればいいんだけどねー
円グラフはどうも許してくれないらしい。

わかりやすく式で説明すると
円をあらわすn個のxとy=√(1-x^2)に番号iをふってxi、yiとする。
(√(∑(xi^2+yi^2)))/n　(i：1～n)
と
√((∑(xi^2+yi^2))/n)　(i：1～n)
は違うし
√((∑(xi^2+yi^2))/n^2)　(i：1～n)
としてもムダなのよ！

横軸はあくまでxであってx^2ではないし、縦軸もあくまでyであってy^2ではないからね。
平均した数値グラフをも円にしたければ、(√(∑(xi^2)))/nと(√(∑(yi^2)))/nの関係が円になるようにすることね！
ってこってす。おーまいこってす。




そしたら仕方がないんで、相加平均やめて、相乗平均にしますか。
足し算して割る代わりに掛け算してルートとか取るアレ。

xを実部、yを虚部に置き換えた複素数zの相乗平均だったら、
偏角が相加平均になるから、どうがんばっても円になるでしょ。
っていうか円の方程式上に乗るでしょ。
どうせ半径1だし。楽チンだなぁー



そんなわけでぇー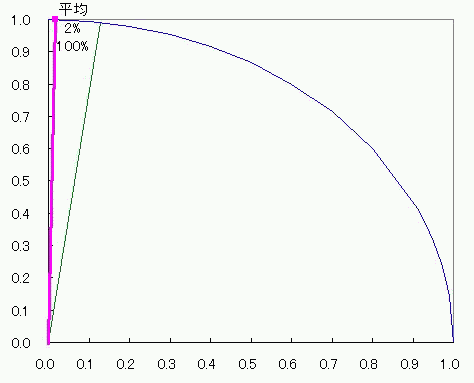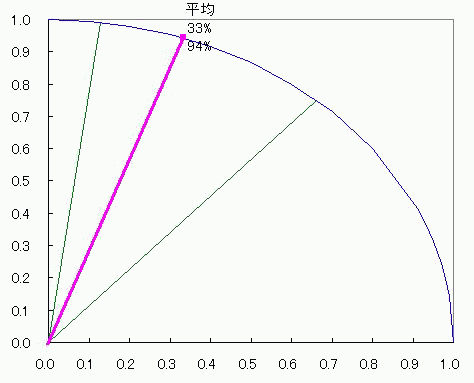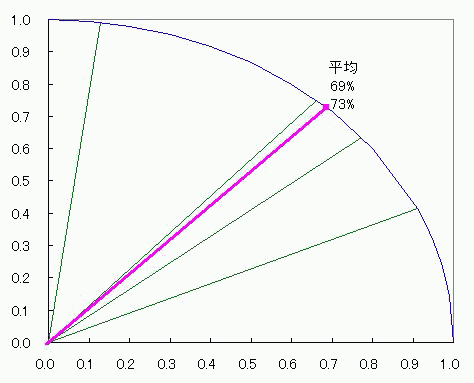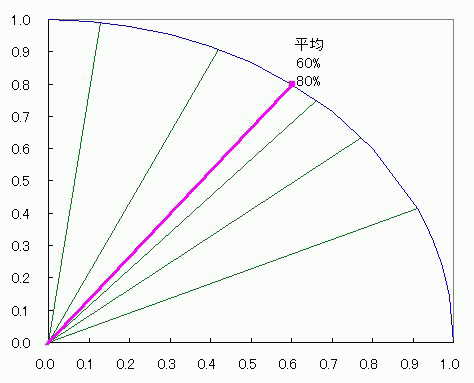

こんなんでましたけどもー！


2つの針の和は最大141V(歌：いとうかなこ)　スカイクラッコの観測者問題

にほんブログ村

GCD：技術的な学校のかいだん(最大公約数)

技術的な学校の、怪談
で分けるべきか
技術的な、学校の階段
で分けるべきか

まず困ると思います。
っていうか困ってください！
困ってもらわないと困ります！！＞＜

11段ある！

SFをほとんど読まないきのこさんは
11人いる！っていう作品のジャンルをホラーだとずっと思っていました。
SFだったんですね。



宇宙の医学では、男性は11の倍数、女性は10の倍数のインチでセンチメンタルになるといわれています。

にほんブログ村