|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
エクセルでアニメといえば閏秒ですよね
閏秒の問題は「(なう関数-きょう関数)*1000000」とかやってエクセルでアニメを作ろうとした際に菱々と感じたのですが 意外とシビアな問題なんですよ。 厳しいではなくシビアといったところがミソと自分で言います。 厳しいという言葉は問答無用で好きじゃないんですよ、むしろ嫌い。 厳しいのとにかく大っ嫌い。うん そこでシルバーっぽい渋屋なシビアを使ってみたら で。 たとえば何らかの理由で1日に342秒挿入するとするじゃないですか これが340秒ではなく342秒だったり、300秒じゃなくて342秒だったりってところが実は意外と問題になってくるのです その理由を説明してみます 今ここに、11秒周期のアニメーションがあるとします。 このアニメーションは、「その日の現在の時刻を取得する関数(なう関数 テキトーな空セルを選択したままdelキー押しっぱなしで、再計算するたびに現在の時刻を返すわけですよ APIもマクロもナシでミリ秒余裕でした。 「その日の」現在の時刻です。 1日経つと0にリセットされます。 じゃあ1/1の23:59:59から1/2の0:00:00にかけて、アニメーションは正しく動作するでしょうか? 実は正しく動作しません。 1/2になった時点でアニメーションが「跳び」ます なぜかというと、このアニメーションの周期が11秒だからです。 1日24時間、つまり86400秒は11の倍数ではないからなのです。 たったこれだけの理由で誤作動するのです。 しかし、これが「その日の現在時刻」ではなく 「日付も含めた現在時刻(なう関数オンリー)」だったらちゃんと動くんですよ 1/2になった瞬間にリセットされませんからね。 もし、あくまで「その日の」現在時刻でアニメーションを動かす場合は 真夜中に誤作動する問題は割り切って諦めたほうが賢明でしょう あるいは11×86400=950400秒の周期で「どちらでも割り切れる」ような周期にすればそりゃぁ正常に動きますが、 そんなのは 「ケーキを分度器でキッチリ7等分できるようにするために360×7=2520進数で、一周2520度の分度器を作りました!」 くらい切りのないことだと思いますよ!!!1 だからたとえば、1日に342秒追加するか340秒追加するか大晦日まで議論しているとすると 調整側から見れば いい迷惑なのでさっさと決めてしまってください ということなのです。 その下1桁のたった2秒が文明崩壊の除夜の鐘になりかねないのです エクセルでアニメする人はあまりいないかもしれませんが 今の世の中は意外と、そんなエクセルみたいなので管理されたアニメにわりと近い状況なのです リアルはいつだってアニメよりもおかしいのです そういえばミリ秒取得関連で、APIには「パソコンつけっぱ四十九日問題」というのがありましてね、より正確には49.7日問題なんですが以下本題 サーガ ペイン  にほんブログ村 PR
前にドラクエのドーナッツな世界観のことを書いた日記で
図の代替テキストにドーナッツやらトーラッスやら代替埋め込んでおいたんだけど あれからどーも気になって、全部の組み合わせをシラミつぶしたいっ! ってずーっと思ってたんだよ。 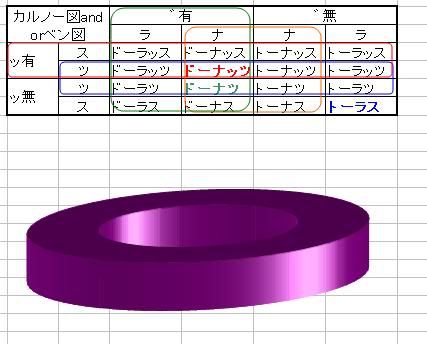 バイハオザードの組み合わせパズルなんかも、全組み合わせを網羅するアルゴリズムを確立しないと気がすまないタイプ  にほんブログ村  狼と香辛料の主題歌がまんまゼーガって話を聞いたのがもう数年前かな 香辛料とはいまだに縁がなく、ROCKY CHACKさんの歌もゼーガEDしか知らないんだけど この「ROCKY CHACK」って字面になぜか親近感を感じたんだ。 ckychckっていうかさ、cとkとyとhのヘンな使い方が僕のローマ字のヘンな使い方に似てるんだよ でも僕の場合CHACKYって1ワードにしちゃうかも とも思った。 2ワードのほうが語呂がいいとわかっていながらも1ワードによせ集めたいっていう妙な癖がね そうだ、じゃあCHACKY JENにしたらどうか いやいや、そこはCHACKY J¥nENにして46億円なのか46億年なのかよくわからない感じもいいかもしんない そういえばhtmlだと改行は<br>とかになるよね。 ところで、エクセルに1e8って入れたら1億になるけど 1e8+1ってやったらどう演算が連結されるのかな あ、1e9じゃなくて1e8のままだ。っていうか1億飛んで1の近似値だな。やっぱ+は結合法則的に見てカヤの外か。 よかったよかった、予想通りで一安心。 そういえば、1e^n±1の倍数ってどいつもこいつも見つけやすいんだよなー 10進数の必然なのかなんなのか知らないけど。 10^1+1=11の倍数は1桁ごとに区切って奇数桁目の合計と偶数桁目の合計との差が11の倍数になれば11の倍数だし 例: ・121の奇数桁目の合計は1+1=2、偶数桁目の合計も2 ・506の奇数桁目の合計は+6=11、偶数桁目の合計は0だから、合計同士の差が11になって506自身も11の倍数 ・165の奇数桁目の合計は1+5=6、偶数桁目の合計は6だから合計同士の差が0になって165自身も11の倍数 10^2+1=101の倍数は2桁ごとに区切って奇数ブロック目の合計と偶数ブロック目の合計との差が101の倍数になれば元の数自身も101の倍数だし 例 ・1414の奇数ブロック目と偶数ブロック目はそれぞれ14だから1414は101の倍数 ・100899の奇数ブロック目は99と10、偶数ブロック目は8、99+10-8=101なので100899も101の倍数 10^3+1=1001の倍数は3桁ごとに区切って奇数ブロック目の合計と偶数ブロック目の合計との差が1001の倍数になれば元の数自身も1001の倍数だし 例 ・1112111の奇数ブロック目は111と1、偶数ブロック目は112だから合計同士の差は111+1-112=0なので1112111自身も1001の倍数 以下同文 じゃあ10^n-1は? 10^1-1=9の倍数は、各桁の合計が9の倍数になれば元の数自身も9の倍数だし 例:123456789は1+2+3+4+5+6+7+8+9=45で9の倍数だから123456789自身も9の倍数 10^2-1=99の倍数は、9の倍数でありかつ11の倍数なら99の倍数なんだから、見つけやすいし 10^3-1=999の倍数だって、9の倍数であり111の倍数なら999の倍数なんだから見つけやすい けども、111の倍数の倍数判別がちょっと曲者か。 いちおう111自体が3の倍数なんだけど、111/3=37ってヘンな素数だからなあ 3の倍数かつ37の倍数であれば111の倍数でなんだけど 37の倍数かどうかを見分ける方法ってのがチョイ面倒なんだよなぁ 10^4-1=9999の倍数を見分けるコツは実は999ほど難しくない 9の倍数でありかつ1111の倍数であればいいんだけど 1111が11の倍数で、101の倍数でもある。 ぶっちゃけ11×101が1111なんだけどね。 11と101の倍数の見分け方はさっきやったもんな 10^5-1=99999の倍数は 9の倍数でありかつ11111の倍数でもあればいいんだけど 今度は11111の倍数かどうかってのが見分けがつきにくくなるんだよな 素数判定したら41と271に素因数分解されたけどこれでどないせっちゃねんって感じだな そうすっとあれか 10^n-1の場合はnが奇数だったらそんなに見分けがつきやすくないってことになるのか。 いや、そうでもないな。 10^n+1は全部見分けがつきやすい 10^n-1はnが2のべき乗に親しいほど見分けがつきやすい (※ただしnは じゃあn=0ならどうなる? 10^0-1=0 ああこれじゃ倍数の意味がそもそもねえな そういえば10^0+1=2の倍数について考えてなかったけどこれは偶数そのまんまだな。 でもまだ諦めるわけにもいかない 0の向こう側も確かめなければ。 10^(-1)+1=1.1 10^(-1)-1=0.9 10^(-2)+1=1.01 10^(-2)-1=0.99 10^(-3)+1=1.001 10^(-3)-1=0.999 って、これnが正の数のときと同じじゃん 1.1は11だし、0.9は9だし、1.01は101だし、0.99は以下略 小数の倍数ってのもミョーな感じだろうが、小数で割り切れるかどうかに比べればなんてことはない つうことは (※ただしnは ↓ (※ただしnはゼロを除く整数 nが小数、無理数、複素自然数、複素整数、複素有理数、複素無理数などの場合は疲れたので考えないでおこう d/dt(∂L/∂vx)=∂L/∂x d/dt(∂L/∂vy)=∂L/∂y まるっ。  にほんブログ村
先日機種変したケータイにようやっと歩数計のハードウェアがきましてね
そのソフトも素敵に充実しているのです。 1日ごとの歩数を記録してくれていて 丸々2ヶ月分くらいは溜め込めるみたいなんすよ リストやグラフ表示もあり、 歩幅から歩行距離、 歩行距離と体重から消費カロリー 消費カロリーから脂肪燃焼量も同時に表示してくれる優れものなのです! さて、この歩数計のデータを取り始めてから20日が経過し、データもいい感じに揃ってきたので、解析をしたいと思うのです。 歩数と歩幅があったら、歩数×歩幅から歩行距離は簡単に出せるじゃないですか 消費カロリーから脂肪燃焼量を計算するのも、係数は一定のようでした。 アインシュタインの特殊相対性理論による 化学反応による質量-エネルギー変換効率・脂肪燃焼量・光速の2乗=消費カロリー の式から「化学反応による質量-エネルギー変換効率」を換算すると、0.000000000325(3.25A(ストローまないオング))と算出できました。 化学反応だとだいたいそんなもんですよね 核融合だとスーパーセント、核分裂は忘れましたが、ブラックホールエンジンの100%との間に降着 ただ、何キロ歩いたら700kcal消費するのかっていうのがあんまり一筋縄じゃなかったんですよねー 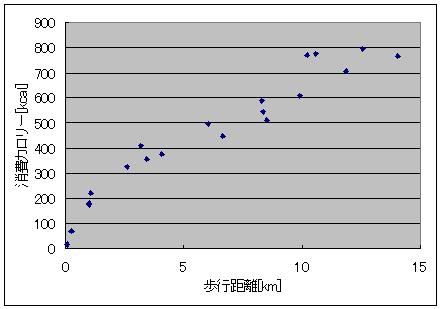 とりあえず、74kgの物体が12kmくらい歩くと700kcalのカロリー消費になって、100gくらい減るらしいんですが、 消費カロリーが単純に歩行距離に比例するってわけでもないようで・・・ 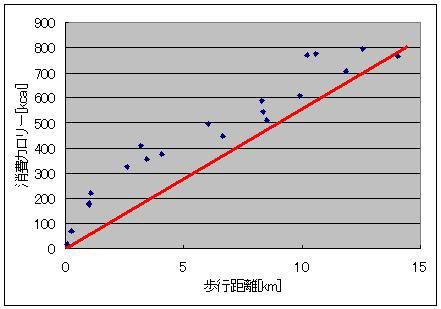 そこで、単純に摩擦に抗ってある体重の物体がある距離を移動した際に使うエネルギー(=仕事量)を摩擦係数から計算すると仮定して計算してみますと(イメージとしては、さっきの図の赤線を水平にして見たimage.jpgです) 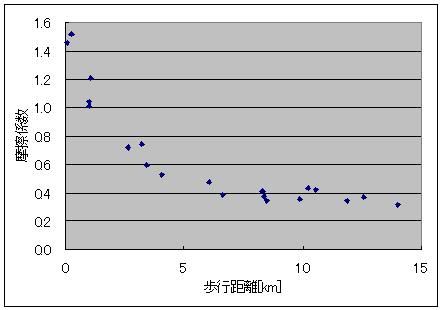 これがまた歩行距離に応じて摩擦係数が微妙に変わるとか言うおかしな計算をこの歩数計はしてやがるみたいでしてね しかも結構ギザギザなんすよ! もしかして、一度にまとめて歩いたかどうかも考慮に入れてくれてるんでしょうか 歩いているうちにだんだんカロリー消費が緩慢になってくるみたいな感じの。 摩擦係数でいうと、だんだん体があったまって潤滑が進んでくる感じです 歩き始めは1.5あった摩擦係数(仮)も、6kmを過ぎると0.5近くまで下がってくるわけですよ それで、少し間を空けてまた歩き出すと潤滑が元に戻ってしまうので 同じ歩行距離でも消費カロリーが微妙に違ってくる、みたいな。 まあ摩擦係数が1以上っていうのも変な話だと思うんですけどそこはまあ 平坦じゃないガタピシを関節ギシギシ滑らせて無理やり摩擦係数として換算した みたいな状況だとそう算出されてもおかしくないのかなーってかんじ 摩擦係数のだいたいの数字が1を下回っててホッとしたようなそうでもないような。 ===  で、出てきたこのグラフ 今度はこいつを1つの式で近似してみたいという欲求が沸くわけですよ普通は  そこで登場するのが両対数グラフです。 x軸もy軸も目盛が対数になってるグラフで、0.1の次の目盛は1、その次の目盛は10、さらにその次が100となっている不思議グラフです。 両対数グラフはy=x^nのnがプラスでもマイナスでも小数でも、つまりxの何乗に比例しようが直線で表現してくれる便利なグラフです 普通のグラフでは、y=axの傾きがaをあらわしているのですが 両対数グラフでは傾きがy=x^nのn、つまり何乗に比例するのかをあらわしています。 ※ただし、y=ax+bのbのような余計なものがついてるとちょっと邪魔です 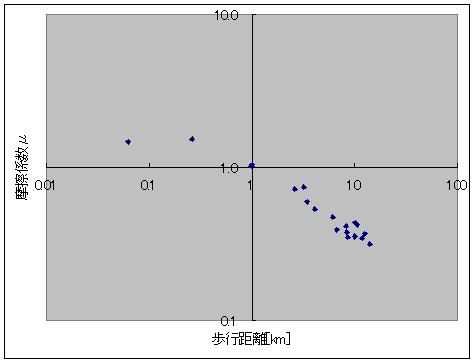 なんかこれどっかで見たグラフですよね あれすか、アンプ増幅度の周波数特性のボード線図の折れ線近似ですか まあそんなわけで、このグラフの右側の坂の(両対数での)勾配(傾き:slope関数)を計算することで、どういうわけか歩行距離500m(時定数じゃなくてωRCのRCみたいなあれなんだっけ、折れ線の折れポイントのことなんだけど)以上の領域では摩擦係数が距離のマイナス0.45乗に比例、つまり0.45乗に反比例しているという結果が出ました。 なんで0.45乗なんでしょうね、そんなことはしりません^^ そのうちググれれば御の字でしょう 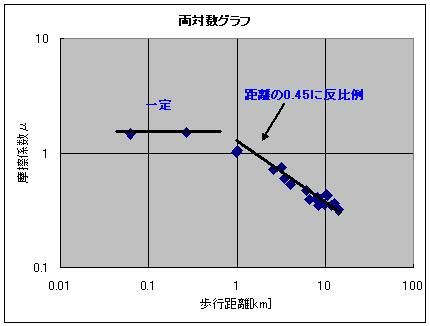 ただ、歩行距離が500m以下の場合はなんだか定数っぽいので 単にx(歩行距離)の-0.45乗ってわけでもないのでしょう そんなときは(1+x/x0)^(-0.45)としてx0を調整してグラフに合えばいいのです それでも形だけ合って上や下にシフトしているときは式全体を何倍かしてやればいいです。 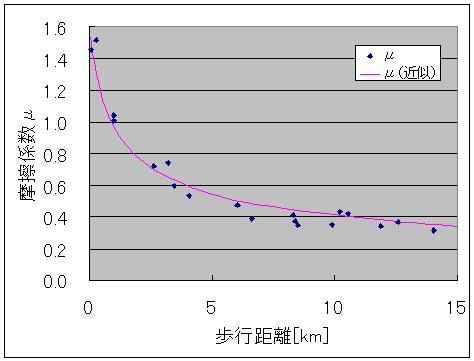 結論 摩擦係数(仮)=1.6×(1+距離/500m)^(-0.45) という近似ができました^^ つゆうことは、 歩数から軽くなったであろう体重を計算したい場合は 歩行距離=歩数×歩幅 消費カロリー(そのまま計算するとジュールで出るのでカロリーに直す)=摩擦係数×体重×歩行距離 摩擦係数=1.6×(1+歩行距離/500m)^(-0.45) ダイエットしたカモシレナイ体重=消費カロリー(calをJに直す)/(3.35ストローまないオング×光速の2乗) で計算すればいいわけです^^ ハイパーーーー ス フィルタ  にほんブログ村
絵や図面を描くときに、1点透視図法ってあるじゃないすか。
消失点を適当に決めて、そこに向かって奥行きの線を集中させる描き方っすよね それに対して、簡易な描き方として等角投影法ってあるじゃないすか たとえば3次元の物体(ベクトル)のデータをエクセルに打ち込んで、それをx、y、z軸で適当に回転させて ベクトル要素3つのうち2つを折れ線グラフで結べば、等角投影法っぽく見えるじゃないすか そのデータをですよ 1点透視図法に変換させたいと思いましてね そうすると、消失点に向かうようにっていう理屈は定量化可能なんすけど 奥行きの定量化って自分、あんまりよくわかってなくてですね それで日食のことを思い出してたんすよ。 太陽って月の約380倍遠くにあって、大きさ(半径)も月のちょうど約380倍あるから、遠近法的に見て同じ大きさに見えるわけじゃないすか ってことはですよ、2倍遠くにあるものは半分の大きさになるわけっすよ じゃあ、消失点まで同じ長さのサイコロが無限に積まれていくとしたら 一番手前のサイコロを描く際に、紙面で言う消失点までの長さの何割の長さで奥行きを描けばいいんすか ってことで無限等比級数の話になってたんす。 等倍のサイコロが一番手前にあって、1/2のがその1個奥にあって、1/4のがさらにその1個奥にあって・・・ ってことは、紙面上のサイコロの奥行き長さを1とすると、消失点までは∑(1/2^k) (k:1~∞の整数) になるわけじゃないすか。 無限等比級数っすよ、懐かしくね? wikiるまでもないっつうか、wikiったら負けな気がするので導出するっすよ。 1+1/2+1/4・・・+1/2^k ってのをaとするっすよ で、a/2を考えるっす。 a/2=1/2+1/4+1/8+・・・+1/2^(k+1) になるっすよね。 じゃあa-a/2をしたらどうなるっすか 左辺はもちろんa/2 じゃあ右辺は? 途中のモブがバッサバッサ切り倒されて 1-1/2^(k+1) じゃないっすか。つまり a/2=1-1/2^(k+1) ここでは無限等比級数っすから、k→∞の極限で考えてよかっす つまり、a=2 そうすっと、消失点までの長さは、一番手前のサイコロの紙面上の奥行きの長さの2倍になるわけじゃないすか これでようやく奥行きの定量化も済んだってわけっすよ。  にほんブログ村
仲人には仲人の紛らわしさがあり
別れさせ屋には別れさせ屋なりの紛らわしさが、ある。 光で電気信号をカップリングさせたいフォトカプラと、光で光をカップリングさせたい光カプラ かたや 電気信号を物理的に分離させたい変成器と、電磁波を使って電気的に分離させたいアイソレータ ぐぬぬ・・・これじゃウィルスと免疫のイタチループ・・・!私たちは乙女! そう、花も恥じらう乙女だったはず! それなのに・・・普通の女子工生みたいな会話もできないんだもん!スラマッパギー!  ところで、アイソスピンやアイソトープなどの愛想とはなんなのだろうか、国際標準化機構のことだろうか  にほんブログ村
昔、降水量というものの定義を勘違いしていたことがあった。
単位の毎時mm(ミリメートル)だけを見て 「降った雨が周りに抜けていきつつも、どのくらいの深さまで貯まっているのか」 というものだと勝手に勘違いをしていて 「ちゃんと水の体積で測ればいいのに」 と思っていた。 しかし実際はちきんと体積で定義されていて ミリメートルという長さの単位は体積を地面の面積で割った、単位面積あたりの体積(毎時) なのだと気づくまでに数年かかった。 実は降雪量についても同様のようで、単位が毎時cm(センチメートル)、つまりミリの10倍になるのは雪や水の密度などによるもので、同じ重さでも体積が増すからなどの理由があるらしい。 水自体は水(液体)から氷(固体)になる(相転移)際に密度を減らす珍しい物質であり さらにその氷がより集まった雪も全体として密度が減っている。なんとなく興味深い。 しかし、積雪は体積ではなく深さ、つまり純粋に長さの物理量である。 元々僕が考えていた「一部抜けつつもどのくらいの深さまで貯まっているか」の概念に近い 降水・降雪は降水「量」・降雪「量」などと呼ばれるが 積雪は積雪「深」と呼ばれる。 しかし紛らわしいことに積雪「量」とも呼ばれることがあるらしい。実に紛らわしい まあ物理量なのだから仕方がないのかもしれないが、なんかこうないのか 深はいいんだ、問題はむしろ量のほう 積雪体・・・積雪積・・・積雪体積・・・そもそもたかが物理量の1つでしかない体積が物理量全般の量の称号を得ているのがなんとなく不条理っぽい しかし、こうして紛らわしさに気づくことで 改めて自分がどういう勘違いをしていたのかがようやくわかることもあるんだなぁと思った。 勘違いをしていた当初は、何をどう勘違いしているのかさえ漠然としていることが多い。  ←これは雪です!雪なんですよ!(`・ω・´) ←これは雪です!雪なんですよ!(`・ω・´)にほんブログ村
先日、半導体の電子回路でアイソレーションやインピーダンスマッチングは可能かという話をした。
結局のところ、インバータやコンバータやPWMの昇降圧チョッパといったものを限定的に使用すると インピーダンスマッチングをしてアイソレーションが可能であることがわかった。 ところで、チョッパというのはいわば、直流でも行えるトランス(変圧器)のようなものだ トランスは古くから使われており、交流において動作するが 電流と電圧を負荷に合わせると言った意味では、トランスでインピーダンスマッチングというのもできておかしくないはずだ。 そこで、過去の教科書を引っ張り出して変圧器の自己インダクタンスと相互インダクタンスが インピーダンスマッチングされる際にちゃんと相殺されてインピーダンスがちゃんと実数になるのか計算 したかったんだが、wikipediaを見たら「マッチング用の変圧器は特に変成器と呼ぶ」 と書かれてしまっていたので計算する気が失せてしまった。 残念ながら僕もそんなに暇じゃないんだ アイソレーショントランスとはまた別だと思うんだけどどうか。 アイソレーショントランス:電気的に絶縁された変圧器→手段 変成器:電気的に絶縁しているように見せかけるための変圧器→目的 なんじゃないかなぁと つまり組み合わせてアイソレーション変成器があってもいいのかな?とか思ったり。  にほんブログ村
CタケPマンなんて「神が破った
それこそ宇宙自体が「神がネルトンした子宝」じゃんか! 神がつくった究極の素粒子 レオンレーダーマン なにこの名前ウケるwww レオンレーダーマンって名前の素粒子なのかwwwwwレオンがライダーマンみたいwwww 仮面がピコーンピコーンってレーダーみたいにwwww噴くwwww ・・・え、著者名!? でもウケるwwwwwなんかウケるwwww 図書館で笑ってはいけないらしい やばい宇宙エロい!  にほんブログ村 以前の日記、 ラピュタ庭園の壁と光アイソレーション と 直流アイソレータというものは で、画像のような 外からは白く、中からは透けて見える壁 をどうやったら作れるか ということをアイソレータという電子部品を絡めて書いたことがある。 実際問題、 ラピュタの壁ようなこれを実現するのはかなり難しいというか不可能に近いのだけど 昔、会社の先輩に 「アイソレータとダイオードってどう違うんですか?」 と聞かれて、予想していた質問に案の定答えられなかったときのことを思い出した。 「ダイオードは電流の一方通行、アイソレータは電磁波、つまり電気的エネルギーの一方通行なんだよ」 と言ったところで、電気が分野ではない先輩には通じない説明だとはわかっていたので 無言になってしまってごめんなさい。 その質問を受けてから1ヶ月ほど、アイソレータについてのマイブームが訪れ wikiを見ると半導体のアイソレータもあるにはある。と書かれていることに驚いたのもいい思い出。 まさかそれってダイオード的な・・・と恐る恐る思い、結局当時は答えを得ることができなかったのだけど 最近になってLED照明の購入を吟味していたとき 偶然にも「調光用の電源は使用しないでください」の説明の文字を読み センサによるスイッチングと何が違うのかと思って最寄の電気屋のおっちゃんに聞いたら 思いのほか電気屋のおっちゃんが電気屋で(エンジニア的な意味で)  超光戦士シャンゼリオン 超光戦士シャンゼリオン「調光するやつは 習った当時はサイリスタと行列の積が許せなかった そんな不条理をも道具として利用してしまう人類も許せなかった なんていいやがるもんだからちょっと(ノーテン)キラキラしちゃって 答弁の最中は意味がわからなかったんだけど 要はPWMによる昇降圧チョッパのことを言ってるんだなと理解、そりゃぁ1Hzを境に全然基本周波数が違うから トニートニー 半導体の寿命の意味で考えると明るさ・人感センサーによるスイッチングと調光によるスイッチングは全然別物だよなぁ という結論に至った。 つゆうことは、負荷の見かけのインピーダンスを変えられることにも相当し 電源から見た負荷インピーダンスは整合(マッチング)され 負荷から見た電源の内部インピーダンス(内部抵抗?)も変化しているはずだから これは実質、電子回路を用いたアイソレータと等価じゃん! ってことになって、なんかつながった気がしたんだ。 ちなみに、ほとんど直流のインピーダンスマッチングを進行波と反射波のパルスの合成で表現するとこうなる。 負荷開放(インピーダンス∞)がこうで 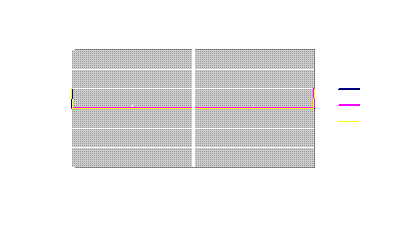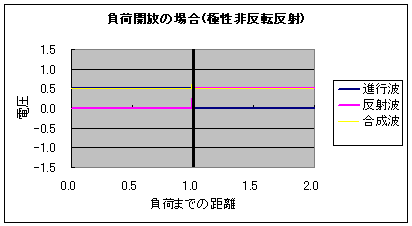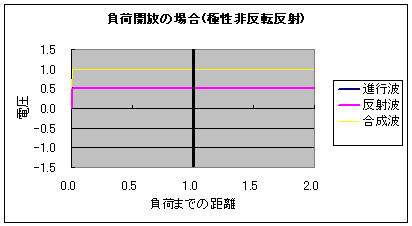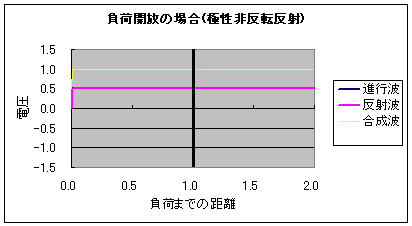 負荷短絡(インピーダンス0)がこう 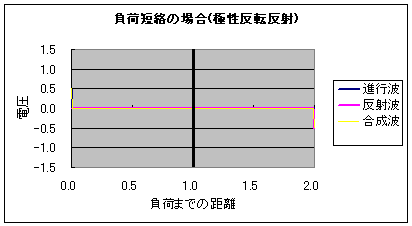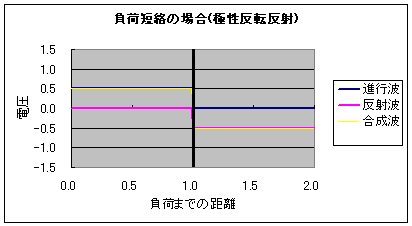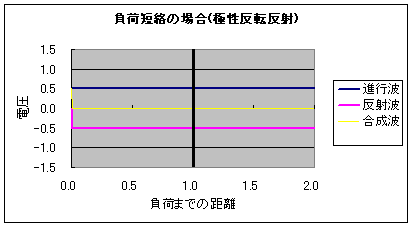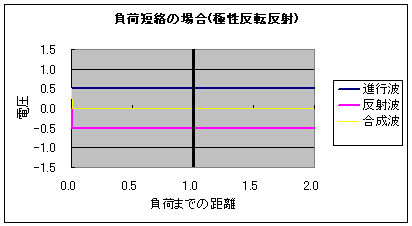 マッチングされてると反射波がなくて、エネルギーの全部が負荷に費やせるわけ。 (※負荷までの距離の数値が間違っています。真ん中の黒い縦棒が負荷です)  にほんブログ村
がーーーーー!
俺のバカの壁がーーー!崩落したーーーー! 循環参照・・・コイツ・・・できる・・・っ!!!1 怖いものも怖れずに積極活用・・・ まずは振り子の ぎゃああああああニュートン法や二分法も簡単じゃねえかああああorzorzorz  にほんブログ村
前回同様、2進数の0.0001(10進数の1/16)の
小数点以下4桁目を その小数点以下3桁目を その小数点以下2桁目を その小数点以下1桁目を 四捨五入の連鎖は危険であるといえる。 もし、0.0001の小数点以下第3位を四捨五入して小数点以下第2位表示にしたい場合は 0.0001の小数点以下第4位を四捨五入した0.001を参照してはならず 0.0001の少なくとも小数点以下第4位以下までの情報を保有する、 つまり0.0001000・・・の小数点以下第3位「0」をいきなり参照して、0.00としなければならない また、3進数や5進数などの奇数進数では繰上りまでの数が奇数になって 2進数の0捨1入や6進数の2捨3入などのように半分ずつに出来ず 状況はもっとややこしくなる ような気がする π進数など無理数進数だったら・・・そんなことはありえるのか?  にほんブログ村 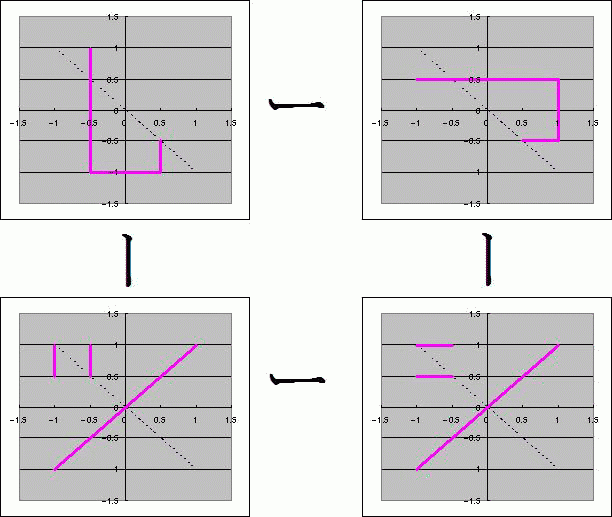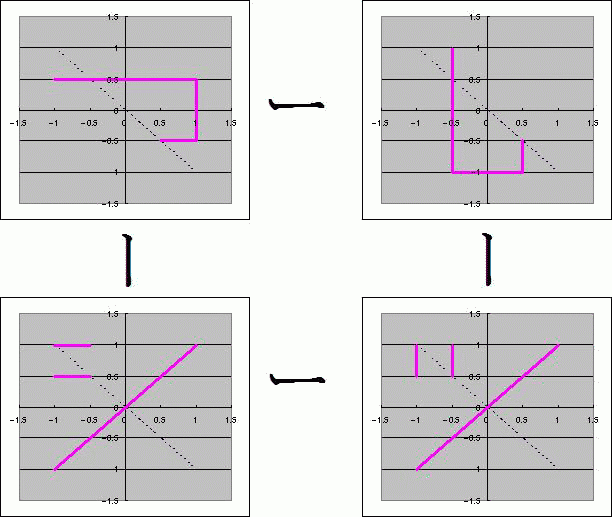 ひらがなの「し」とカタカナの「シ」、ひらがなの「つ」とカタカナの「ツ」は 「つ」と「ツ」はあまり似てもいないのに、なぜか「し」と「つ」は互いに逆関数のような関係にあり 「し」と「シ」はあまり似てもいないのに、なぜか「シ」と「ツ」も互いに逆関数のような関係にある 点で共通している。 なんとなく不思議に思える。 逆関数そのものではなく 反転させてから90°回転させると「シ」は「ツ」になり、「し」は「つ」になる。 反逆関数とでも呼ぼうか。 しかし、反逆関数という名前はずっと昔に一度考えたことがあったような・・・ ちなみに、「ー」はひらがなにしようがカタカナにしようがJISコードでは8508で共通らしい まるでy=マイナスxやy=0の直線のようではないか 裏返って値切るので誰かいりませんかー・・・  にほんブログ村
静電気除去したかったから電気店に寄ったら売ってねえってさ。
なんで静電気対策グッズが電気店になくて100円ショップにあんのよ。 100円ショップの品って時々説明もメーカー表示も怪しいのあるから どうやって静電気除去したらいいのかわかんないまま買って 「これ使えねー」って困るお客さん増えるじゃん>< え、ブレスレットとキーホルダーサイズの棒と、スプレー・・・? どういう原理なんすか・・・原理ちゃんと統一されてるんすか・・・ スプレーはアレか 服の ブレスレットは今のところさっぱりわからん。そのうち興味が出たら勉強する。 なんか分野が違う感じがして拒絶反応が・・・ 鳳テブナンの定理って聞いて鳳の字に社会科的なものを感じて拒絶反応が出るのと同じ原理。 昔、棒で除電実験したしな、棒にしようか。 とりあえず棒はこんなん 金属の棒の先端にゴム。 でもちょっと待て・・・この棒、先端に余計なものがついてるように見るんだけど なんで先端にゴムついてんの。 先端が金属まんまの鍵で静電気除去できるのに なんで先端にゴムついてんの。 あ。 そういえば適度な抵抗値を持ってればいいのか。 完全な絶縁体だと電荷はいつまで経っても逃げてってくれないけど そっか、抵抗値はあったほうがいいんだ。 ジュール熱になってくれるもんな。 鍵で触る効果は、あくまで電流の通り道を広くして「痛くなくする」ためであって、電流そのものが減るわけじゃない 抵抗はこの電流そのものを熱に変換して減らしてくれるんだ 適度な抵抗値か・・・俺と地球の よし買った! 購入後、エスカレータを降りる最中、早速開封して財布に取り付ける。 早速、車に乗って、降りる この雰囲気、この空気感、湿度、間違いなくビリっときそう、ピンチをチャンスに変える男! 鍵の代わりにこのグッズを車の外装に当てて・・・ うわっなんだこのまろやかな静電気の味わい!! これが先端ゴムの効果なのかー!! なにこれちょーレールガンなんですけどー  にほんブログ村 |
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|