FBD：内積(スカラー積)と外積(ベクトル積)の意味合いをオートシェイプで理解するッ！

最近数学ゴリ押し気味ですみません＾＾おはようございます量子きのこです



さて、ベクトルの内積と外積というものを数学で習いましたよね
そのとき、2つの積の定義を習っても、意味合いがよくわからなかった人は多かったのではないでしょうか



ベクトルA(xa、ya)とB(xb、yb)があって
内積A・Bと、外積A×Bというのは具体的に何を意味しているのでしょうか。


内積A・Bの定義はこうでした。

A・B=xaxb＋yayb
そして、それはベクトルA、Bの絶対値|A|、|B|と、AとBのなす角θと
A・B=|A||B|cosθ
という関係がありましたね。これはどういう意味なのでしょか。

エクセルを起動して、オートシェイプで適当にベクトルを2つ、描いてみましょう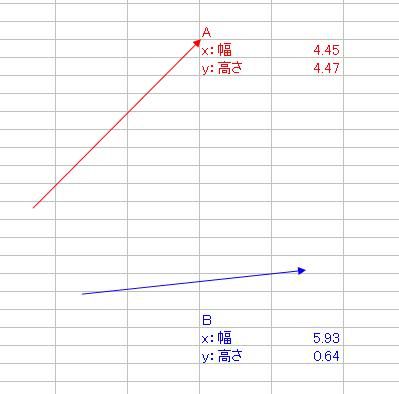

次に、Aベクトルは赤、Bベクトルは青、と色をつけておきましょう
↓
AとBベクトルのサイズをメモしておきましょう
僕の場合は
・A　x(幅)：4.45、y(高さ)：4.47
・B　x(幅)：5.93、y(高さ)：0.64

とりあえず内積を計算します。
xaxb+yaybなので、僕の場合は4.45・5.93＋4.47・0.64=29.2493くらいになりますね
それから、とりあえずそれぞれの絶対値|A|と|B|も計算しておきましょう。
絶対値の求め方は、三平方の定理から
|A|=√(xa2+ya^2)、|B|=√(xb^2+yb^2)

でしたね。僕の場合はそれぞれ
|A|=√(4.45^2+4.47^2)≒6.3074くらい
|B|=√(5.93^2+0.64^2)≒5.9644くらい

それでは、内積A・Bを2つの絶対値|A||B|で割ってみましょう。
A・B/(|A||B|)≒29.2493/(6.3074・5.9644)≒0.77794

これが、実はAとBのなす角度θのコサインだという関係がありましたね。
そこで、AとBのお尻同士をくっつけます。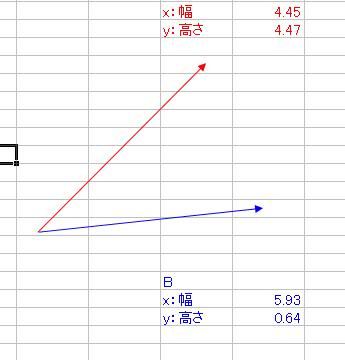


それから、角度を測るために、真四角をベクトルのお尻に添えます。
真四角を少しずつ回転させていって、ベクトルBのお尻にくっつけます。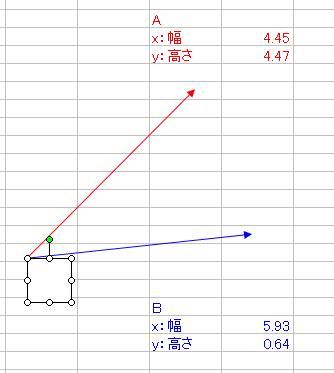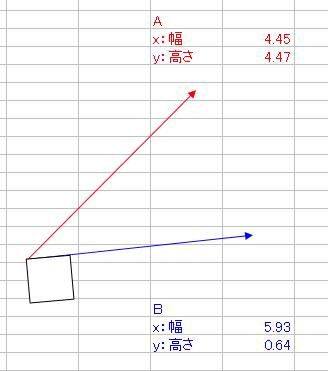
→
そのときの角度、僕の場合は355度が、Bの角度です。


次に、真四角を複製して、Aのお尻にもくっつけて角度を測ります。
僕の場合は315度が、Aの角度でした。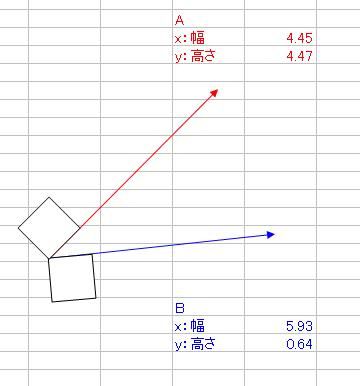

それでは、AとBの角度の差はいくらでしょうか。僕の場合は355-315=40度ですね。
これをθとして、cosθを求めると･･･(※ただし、コサインに入れるのはラジアンに限る)
cosθ≒0.7660くらい

精度は悪いですが、0.8近い0.7で、内積A・Bを絶対値|A||B|で割った値とだいたい合ってますね！





＝＝＝＝＝＝＝
次に、外積の意味合いを説明します。
AとBの外積A×Bはxayb-yaxbでしたね。
これは何を意味するのでしょうか。

ベクトルAのお尻をベクトルBの頭にくるようにコピーしてから平行移動させてみましょう。
同様に、ベクトルBも、お尻がベクトルAの頭にくるようにコピーしてから平行移動させてみましょう。
平行四辺形ができましたね。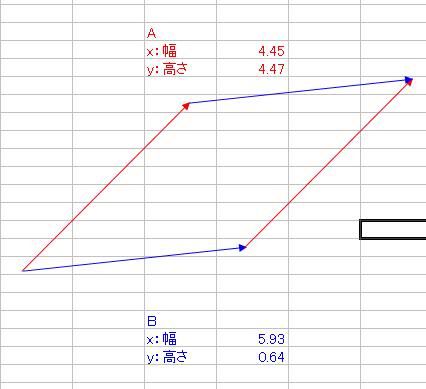

外積A×Bは、実はこの平行四辺形の面積です。
平行四辺形を長方形に変形させて、確認してみましょう。

左側のベクトルAから、水平に線を引きます。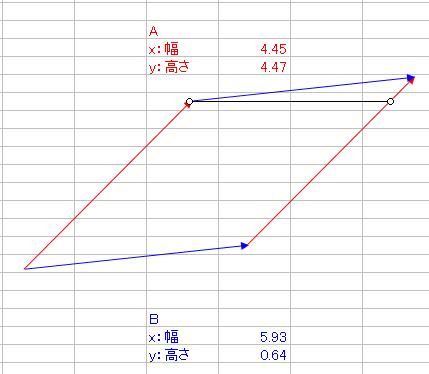

この水平線を、元々のABのお尻に合わせ、
ベクトルAの傾きをそのままに、下の水平線から生えさせます。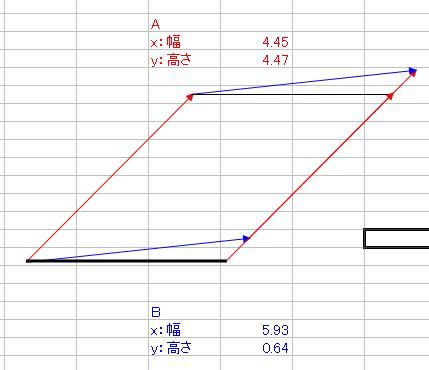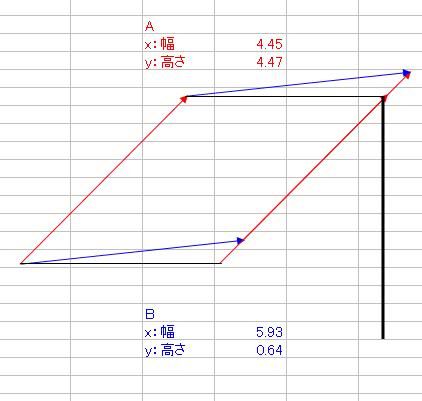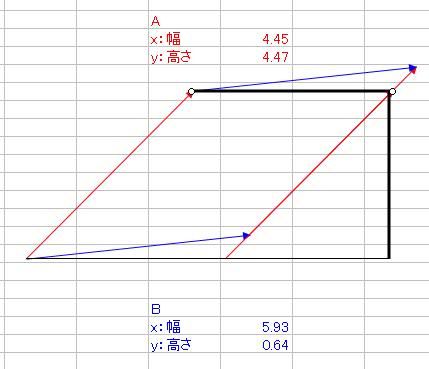
→→
次に、上側の水平線の右側から、よだれ垂線を垂らします。
下側の水平線と垂線の重なるところまで垂線と鼻の下水平線を伸ばします。

ここで、垂線と上側の水平線の長さをかけたものが、平行四辺形の面積になるので、
長さを測ると、よだれ水平線：5.32、はなのした垂線：4.45→面積：23.674くらいになるので
A×Bと比較しますと
A×B=23.6591くらいと、だいたい合ってることがわかりますね。


ただ、A×Bをそのまま計算しますと、マイナスの23.6591になっていることがわかります。
このマイナスは何を意味するのかといいますと、AとBのかけた順番を意味しています。
B×Aの符号、といいますか向きはA×Bの符号と逆になります。

どういうことかといいますと
外積はベクトル積とも言って、スカラー積つまり内積のA・Bとは違って、計算されたものがベクトルになるんです。
一見スカラーのように見えるのは、平面内で外積をやっているからで
画面の手前から奥、あるいはその逆に向かっている成分だけがスカラーのように計算されているだけなのです。

外積A×Bの意味するところは
大きさはAとBが作る平行四辺形の面積
向きは、A×Bとした場合は、AからBに向けて回転する向きと右ネジ(右手)の関係の方向
というものなのです。

今回はA→Bが時計周りだったので、ネジを右に回したら奥に進むように
画面の手前から奥に向かうベクトルとなりました。

ではどうしてこれがマイナスを意味するのかというと
座標系の定め方(約束事)が関係してきて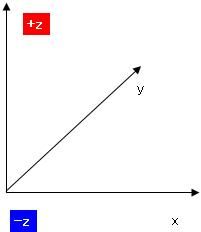

x軸からy軸に向けて回転する方向と右ネジ(右手)の関係に、z軸のプラス方向を定める
と公に約束しているからなのです。これを右手系と言って、
z軸の±が逆向きの左手系よりも右手系のほうを一般的には多用します。
今回の外積は、z軸のプラスの向きと逆向きだったので、外積がマイナスの値になったのです。


ちなみに
3次元空間でベクトルA(xa、ya、za)とB(xb、yb、zb)の
外積をする際にはx、y、z軸の単位ベクトルi、j、kと、
行列C=

i	j	k
xa	ya	za
xb	yb	zb

の行列式|C|とを用いると
A×B=|C|と、効果的に覚えられます。


にほんブログ村