|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
[1]
[2]
∫∫・・・(xn/(∑xi^2)^(n/2))×Π(dxi)
のn-1重積分(ただし∑はi=1~n、Πはi=1~n-1) ・・・ ・・・ ・・・ なんてできるかボケェー!! ま、まあやってやれなくもないんだろうけど 積分の答えなんか質問箱とかwikiとかにわんさかあるかもしれないけど やりたくもないわーーー!>< せいぜいn=3次元と4次元だけでもがくのが精1杯・・・1般化とか1般人としてまじ勘弁 プログラミングで数値計算しろだ? 循環参照ならプログラムよりは見える化・・・やりたくねえ・・・orz期待<<<<不安しかねえ ま、まあ・・・3次元の結果次第では・・・いや、今考えるのはやめよう。  にほんブログ村 追記:あータイトル違ってますね n次元空間における近似的n-1次元物体の間違いでした。 たとえば3次元空間だったら こんな風に長さと幅が10倍ぐらい違う平面を持ってきて この平面物体を帯電させるわけです そうすると、ごく近い距離で受けるクーロン力は距離のゼロ乗つまり距離に依存しないコンデンサ中の電界のような振る舞いをするわけですが ちょっと距離を離すと 今度は平面電荷っちゅうより線電荷のような振る舞いを見せ初めて あたかもアンペールの法則みたいに半径rの円の円周、つまり距離の1乗に反比例する電界が得られるはずじゃないすか そんで、もっと距離を離すと点電荷のように振る舞い、半径rの球の表面積、つまり距離の2乗に反比例する電界が得られるはずっすよね それが一番最初の式の次元数n=3の場合に相当するだろうってわけっすよ 電界∝受ける力Fが F=∫∫(z/(x^2+y^2+z^2)^3/2)dxdy に比例する って感じっす この積分をまず解析的にしないと始まらない。 積分の中身の由来は単純っす (z/(x^2+y^2+z^2)^3/2) は 表面積S∝1/r^(n-1) と z/r をかけただけ。 3次元空間中に、平面的に電荷が広がっている場合 平面の中心からz軸方向(平面と垂直な方向)にzだけ離れた点で受ける電界を考えるわけですが x方向にもy方向にもプラスマイナス対称に電荷が存在しているので 電界のx、y成分は打ち消しあって z成分だけが強めあうだろう っていう推測によります。 ということは、電荷のある平面の任意の点x,yからの距離をrとすると そのz方向成分であるz/rに比例した力を受けるんじゃないかな~って感じ。 で、その係数がn次元空間だとn次元超球の表面積であるn-1乗に反比例するんだろうなーって感じっす。 n次元空間における各電荷からの距離rは何次元だろうとピタゴラス(あくまで平方)が適用できるだろうと推測し 3次元ではr^2=x^2+y^2+z^2 4次元ではr^2=w^2+x^2+y^2+z^2 みたいな感じになるんだろうなーってことっす。 まあ、ここでいう4次元は「4次元目が時間の4次元時空」じゃなくてあくまで空間としての次元が4つあるってことっすけどね 途中ですがちょっとここで保存します。 PR
なんとなーくだけど、距離の2乗に反比例する引力の運動方程式を解いたことがなかった気がする
教科書どおりに、惑星の運動が解かれる過程を目で追ったことはあったけど もうかれこれ15年も前の話で それを数値計算したことも一度もなかった気がするし 1次元の場合に簡単化して解析的に解こうとしたことすらなかったような気がする。 d^2x/dt^2=-K/x^2 を解こうとしたら x''+K/x^2=0 となって、こういう微分方程式を解いた覚えがたぶんない。 どうやって解くんだコレ。 いちおうは非線形ではないだろうが(そもそも非線形微分方程式の定義がよくわかってない自分) 変数変換して解けるもんだったんだろうか。 もしかしたら例題で解いたことがあったのかもしれない。 しかしなんだ、 これをいざ数値計算にぶち込むと どんな初期値でも軌道が発散しかしないように見えるのだけどどうだろうか もしかして1次元には遠心力という概念がありえないから発散しかしないのだろうか 2次元だととりあえず、初期値次第で楕円軌道に収まるみたいだ。 そういえば力が距離の2乗に反比例するのは3次元空間に点としてのナンラ荷(質量or電荷)が存在する場合だった。 理由は球の表面積。 じゃあ3次元空間上に線ナンラ荷(無限の長さ)や平面ナンラ荷(無限の広さ)があったらどうなるか 距離のn乗のnが1つずつ減っていって 線電荷だったら1乗、平面質量だったら0乗(なので変化しない)になるだろう じゃあこれが4次元空間上に浮遊する1、2、3次元状のナンラ荷から発せられる力だったらどうなるんだろうか たぶんn次元上にあるm次元状物体から発せられるナンラ荷による力は 超球の表面積の理論から 距離のn-m-1乗に反比例するんじゃね?って感じ気がする。 そういや距離のn乗(いちおう整数にしとく)に反比例する力は全部保存力でいいんだっけ? 確か、任意の経路で移動させてみてエネルギーが保存すれば保存力なんだよな。 じゃあそっか、n=1次元だったらmで引きようがないから求心力としては意味がないのか。 (マイナス乗に反比例:比例はとりあえず考えないことにしよう) 以前、巡回セールスマン問題の難易度と1次元っぽさの関係とか 生まれつき電車のレールに沿って走る擬似的な1次元人がいたとして彼らに無理数や複素数の概念が発見できるか みたいなことを書いたことがあったんだけど やっぱり1次元は2次元以上に比べて特別な感じがするなぁ 大小関係が定義できるのは1次元だけだし。 次元といえば、単位の規格化ってのが苦手。 っていうか規格化したら次元解析できないから有益かもしれないけど有害だとも思うの。  にほんブログ村
我々人類には「3次元空間に存在している」という共通の自負がある。
そして一部の人間かもしれないが、「時間が4番目の次元かもしれない」という認識も根付きつつある。 3次元空間だからこそ、点と見なした電荷や磁極(や質量)からは点からの距離の2乗に反比例した力を受けるのであり その理屈は電荷や磁極(や質量)から全方向に当配分されて出てきた電気力線や磁力線(や重力線)を「球の表面積」で割る。この「球の表面積」が半径の2乗に比例するところがミソになる。 逆に言えば、半径の2乗以外、3乗や1乗に反比例する力を受けた場合はそれぞれ、 四次元超球の表面積(ただし単位は立方メートル)だったり円の円周に反比例したりするので それぞれ「空間としての」4次元や2次元であると見なすことができるだろう。 たとえば無限に伸びる電線に電流を流したときの磁界は電線からの距離の1乗に反比例する。 この場合は暫定的に空間が2次元であることを示唆しており 重力が空間としての4次元以上に染み出しているとするなら、部分的にでも距離の3乗以上に反比例しているところをキャッチすればいい。 しかし、2乗に反比例だったのをどうやって連続的に3乗に反比例するようにすればいいのか。 答えはもう出ていた。 先ほどの線からの磁場も、無限に伸びる線だからこそ2次元だったのであり 点とみなしたコイルから出た磁界だったら3次元の法則に従うだろう(※ただし磁極は常に双極子として現れる) つまり、近似同士をつなぎ合わせればいいのだ。 点電荷は実は電荷の集合体であり それもよくよく見れば棒状で 意外と鋭い棒だったとすると 遠くから見れば点でも ものすごく近くから見ると線状の電荷のように見えるだろう。 遠方では距離の2乗に反比例する電界として見えるだろうが 近接すると距離の1乗に反比例する電界として見えることとなる。 まるで ということは、質量も同様に4次元以上の「空間」に広がっているとするなら 近似的には重力が距離の2乗に反比例していても よくよく見ると3乗以上に反比例しているかもしれない これが、曲がりなりにも重力の逆2乗と逆3乗をつなぐ橋となる。 実際、 「四次元以上の空間に染み出した重力があるとするなら物体のすぐ近くだろう」 と世間から睨まれている実情と符合する。 近接的に重力が距離の3乗以上に反比例していたら、遠くから見ればあんなに弱かった重力が 近づけばああ、もうこんなにも大きくなって、すごく・・・ブラックホールが作りやすいです なんていう事情にもつながる。 ただ、実際のところどうなのだろう 空間が4次元以上であるといわれても誰一人として人類にはピンとこないという共通の認識があるわけだから 4次元以上の余剰次元はあくまでも3次元以下の空間とは異なった事情なのかもしれない コンパクト化というのは一体どういうものなのだろうか。 我々にはたまたまコンパクト化されているように思えるだけなのか だれかれ構わずどの生命体にとっても普遍的にコンパクト化されているのか。 4次元以上の空間が普通に認識できる宇宙人にとって宇宙の次元はどう映るのか それと、潮汐力が気になる。 磁場がプラスとマイナスのペア、つまり双極子でしか存在できないことを考えると TDN(ただの)3次元空間でもいともたやすく距離の3乗に反比例してしまう。えげつないなぁ これと見分けをつけなくてはいけない。 にしてもなんで点ではなく空間的に中途半端に分布すると2乗が1乗に減らずに3乗に増えるのか・・・? そういえば、時間と空間を合わせて4次元時空とはいうものの やっぱり時間は空間とは異質な4次元目として扱われるらしく 4次元時空だからといってそれそのままで距離の3乗に反比例とはしてくれないらしい ピタゴラスの定理で符号がマイナスなのは時間だけ!  にほんブログ村
シュタインズゲート第あったかもしれない話
「虚像歪曲のコンプレックス」  まゆしぃ「ずっと思ってたんだ♪2人はなんかお似合いだなぁって でも今わかりました。それは2人が、夫婦だったからなのです!」 オカリン「お、おいまさか・・・」 まゆしぃ「行列さんの旦那さんは、コンプくんです!」 複素「・・・はぃ~?」 クリス「それはジョークになってないでしょ。そもそもこの複素が結婚なんてry」 オイラー「ちょ、その発言はひどくね?」 オカリン「説明してくれ。どんな理由でこの結論に至ったのだ?」 まゆしぃ「お店の人が言ってたでしょ?ローテーション、オイラーの公式、オイラ(一人称)!」 クリス「ダジャレ・・・」 オカリン「そんなのが理由になるか・・・」 まゆしぃ「でも、要素を複数持ってる数には行列と複素数があるでしょ?行列で回転するっていったら回転行列でしょ?」 全員「あ・・・」 まゆしぃ「それに、まゆしぃは決定的な証拠を見つけたのです。 回転行列A 
の固有値λを求めるとA-λE 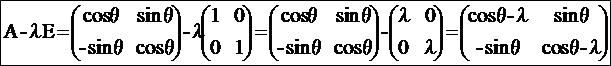 (Eは単位行列)
 (cosθ-λ)^2+(sinθ)^2=0 cos^2θ-2λcosθ+λ^2+sin^2θ=0 λ^2-2λcosθ+1=0 の2次方程式になるでしょ? そしたら解の公式を使って λ=cosθ±√(cos^2θ-1) =cosθ±isinθ=exp(±iθ)←オイラーの公式 固有ベクトルxは A-λx=0が条件だから、行列Aからλ倍のxをかけたものを引いた 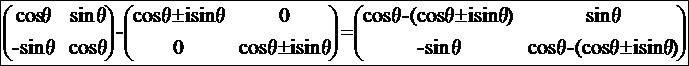
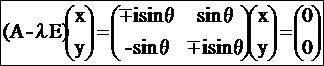 (-1)・(±ixsinθ)+ysinθ=0 -xsinθ±(-1)iysinθ=0 どっちもxとyの比が同じで y=±ixだから(x,y)=(1,±i)(/√(2):規格化するなら) 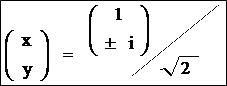 になるでしょ?このi(虚数単位)倍って左右90度回転だから、横軸x(実数)と縦軸y(純虚数)の関係だよね? 」 複素「うわうわうわうわ・・・!」 回転行列「兄さん・・・」 複素「オイラのことは、オニーチャンと呼びなさい!」 クリス「こんなときくらいHENTAIはやめろよ・・・!」  にほんブログ村 オカリン「あれは昔、アーカンソーの草原でその辺の切り株に座っていた数学教師にベクトル(や行列)と複素数は親戚ですか?とたずねたときのことだった。 見るからに大雑把そうなその数学教師はいきなり豹変し、群とか環とか体とかいう古代の中国王朝率いる軍艦巻き(生ではない)のような名前の概念を語り始めた。 5分で俺のキャパはあふれ、とりあえず ベクトルと複素数は親戚かもしれないが生命誕生以降40億年間まったく接点のないほどすごく遠い親戚だから結婚は可能 的な結論を出しておいた。ベクトルのナカに複素数を射れることが出来る。 あれから10年、31にもなっていまだにあえて厨二病全開の俺は、40億年前までタイムリープし、複素数とベクトルの先祖であるアダム微生物とイブ微生物を目の当たりにしていた。 四元数(クォータニオン)という概念があるそうだ。実数を複素数にする要領で、要素を2つから4つにしたような数学的道具のことらしい。4の次は8と続いていくようなのだが、次第に演算が窮屈になっていくのだという。 また、4や8の間の次元は中途半端だからそんなものがあっていいわけがないだろう と主張しているそうだ。 つまり我々の住む3次元空間は中途半端だと言っているらしい。 宇宙は元々もっとキリのいい数の次元で、何かしらの出来事が起こって欠落した次元がこの次元なのだという。 そう主張しているのがどうやら超ひも理論のことのようだ。 あまった次元はどっかに飛んでいったらしい。 思えばこの宇宙は最初と比べて色々と欠落したおかげで複雑多様なことになっているらしい。 現代物理学はそのような欠落を色々と主張している傾向がある。 CP対称性の自発的破れもそうだし、ヒッグス粒子に関する理論も似たような雰囲気を感じる。 元々宇宙の中身に質量などなかったんだそうだ。 それが真空の冷え込みによって水(鉄)が氷(磁石)になるように相が変わり、宇宙の中身である素粒子たちに質量が加わり 質量のあるものは時空をゆがめて重力という引力をお互いに及ぼしあうようになったのだという。 そうして初めて、粒子は群れることが出来、物質という構造が生まれたらしい。 なんともおとぎばなしのような現実ではないか。 ナニ!?「ヒッグス 重し蟹」で今現在ブログを書いているのが俺しかいないだと!?機関の妨害が強まっている!!至急オペレーション・ヘビサイドにとりかかれ!健闘を祈る・・・粒子・ψ・J」
重力を計測する精度が向上していった未来の話
「あれ?重力が反比例するのって距離の2乗と若干違う。」 「え、まじ?そうなの?」 「何乗ぐらい?」 「2乗超、3乗未満」 「曖昧だなぁー」 「だって精度悪いんだもん」 : : : 1週間後 : : : 「2.14乗ぐらいだわ」 「何が?」 「重力反比例。」 「えっ!?整数じゃないの!?」 「なんかねー。てか2超3未満って言った時点でツッコんでほしかった・・・」 「あ、そういえばなんで逆2乗なんだっけ?」 「あれでしょ、空間が3次元だからでしょ」 「あれそういう理由だったの?」 「子供んときやったじゃん。1テラ㌧の点重荷から出る重力線の数は合計で1本。 全方向に放射状に出るから、じゃあ点重荷から1インチキメンタル離れた球体の表面積で割ったら逆2乗則が理解できるよねって。」 「あーあったなー!そういや、重荷が線上の線重荷から出る重力磁場の磁力線の本数は2次元空間で考えるから、逆1乗法則だったんだっけな」 「そうそう。だから今週は球体の表面積を測ってみました。」 「そっちからきたかー!」 「半径1インチキセンチメンタルの球の表面積は、12.6ではなく13.5平方インキチメンタルくらいだったのです!」 「ジャ・・・ジャンジャカジャーン!4πよりちょいでけえ!・・・ん?次元数って整数じゃないの?」 「3.14次元だったりしてなww」 「円周率wwwそれより、小数次元の球の表面積なんて、理論値あったのかよー」 「n次元の球を超球とか呼ぶらしい。そんでその超球の表面積SってのがS=2π^(n/2)*r^(n-1)/Γ(n/2)なんだってさ」 「なんだよそのΓとかってヤツ。key()?」 「ガンマ関数ってヤツで、階乗の親戚だってさ。たとえば4の階乗って4!(ビックリヨン)って書いて、4・3・2・1って1になるまで全部掛け算するっしょ?」 「ああ、総和∑の掛け算バージョンみたいなアレか!」 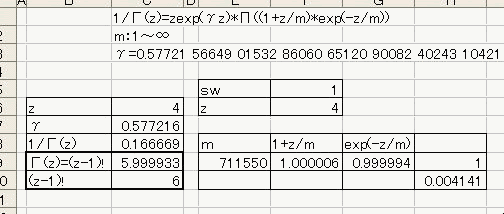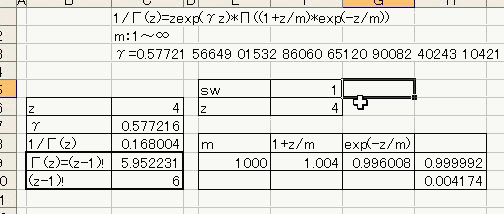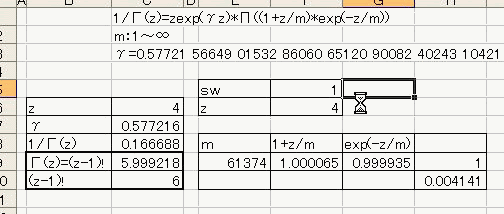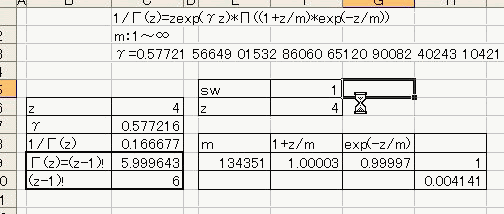 「あれ実は、実数に拡張可能らしいw」 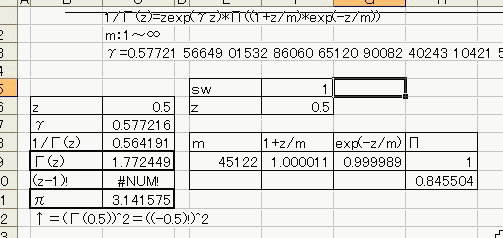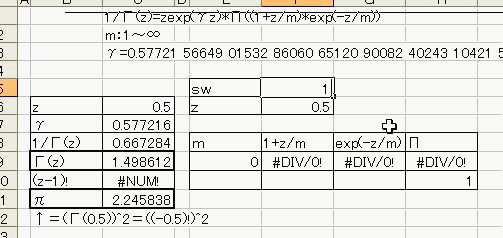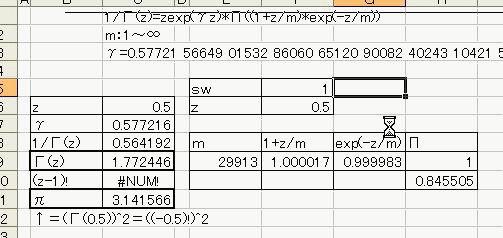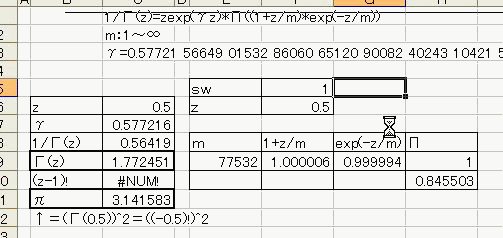 「まじでw」 「しかも、階乗が実数に拡張可能だったら、超球の次元数を整数に留める道理も特にないらしいww」 「えええw」 「※ただし、負の整数は除く」 「なんで負の整数だけハブられてんのwww」 「だって、(-1)・(-2)・・・って掛け算してったら発散しちゃうじゃん」 「さすが数学www常に斜め前を行っててわけわかんねーのに筋だけは通ってるwww」 「ま、ガンマ関数を階乗に翻訳して簡単に書けば、n次元空間の超球の表面積Sは、S=2*π^(n/2)/((n/2-1)!)で書けるってことらしいよw」 : : : 1週間後 : : : 「ちょ、大変なことがわかった。」 「どうした?」 「ガンマ関数の中身は実数に留まってなかった!」 「ぶー∴(゚ε゚ )wwwなにそのタイムリーwww」 「どうかしたのか?」 「俺も似たようなこと考えてたんだよwwπのn/2乗のnが複素数だったらどうなるのかなーってw」 「やってみるか!」 「なにを?」 「ほら、先週の球の表面積、円周率約3.14次元にしてはなんか引っかかったじゃん。」 「ああーあれね。・・・もしかして誤差じゃないってことか!?」 「もしよ?π+i/e次元だったら!?」 「3.14云々+i0.368云々次元ってことかー!」 「ほら、少なくとも表面積の実数部分は13.512でピッタリ。」 「ギャアアア俺たちって無理複素数次元人だったのかよ!」 ======= 補足: 循環参照にまだ慣れていないせいか、複素数まで拡張したガンマ関数の値がおかしいようです 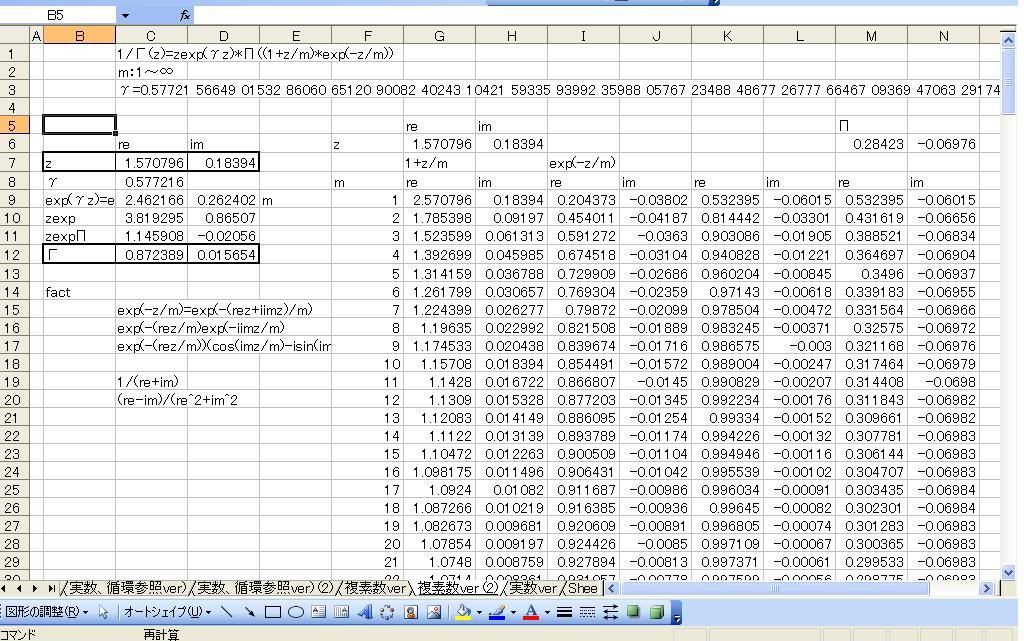 循環参照しないとだいたいうまく計算できるようです。google電卓参照 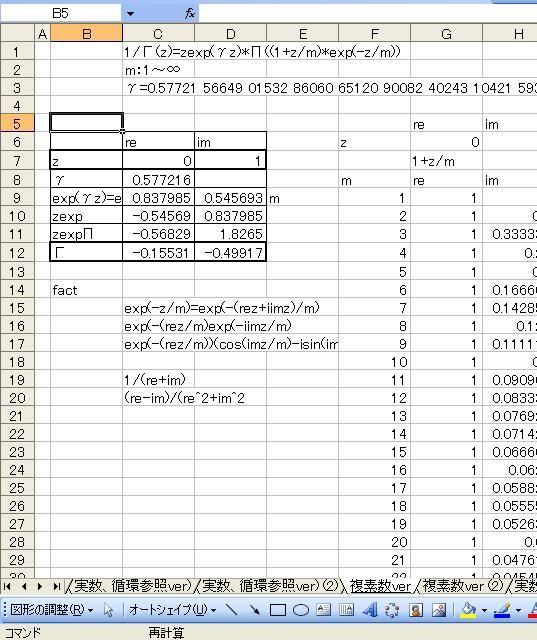 だいたい、といったのは、循環参照してないほうで、虚数単位のガンマ関数Γ(i)を計算してみたところ google電卓の結果と比較して、なぜか実部と虚部とか符号が逆転するのです。 僕の計算にバグがあるのか、wikiかgoogle電卓のほうなのか なんともいえないです。 wikiの3Dグラフは絶対値しか表示してないので、実部と虚部の入れ替わりや符号の参考には使えませんでした なんとなく逆数と勘違いしてるとかその辺のミスだとは思うのですが、ワイエルシュトラスの乗積表示とはつい最近出合ったばかりなので、いまのところ確認の方法が見当たらないです>< ただ・・・、π+i/e次元のガンマ関数は結果的にはだいたい合ってるみたいです^;   にほんブログ村
キーンコーンカーンコーン
よくエクセルで、シート間の集計を3D串刺しとかって言ったりしますけど そうすると4次元目ってなんなんだろう?って思うじゃないですか。 そこから、そもそもエクセルに4次元なんて概念存在するの?って疑問が湧いてきて しばらくは「やーせーぜー3次元空間だろー」 って思ってたりするんですけど ところがどっこり20世紀初頭! エクセルの4次元目は現実と同じ、時間だったんですよ! 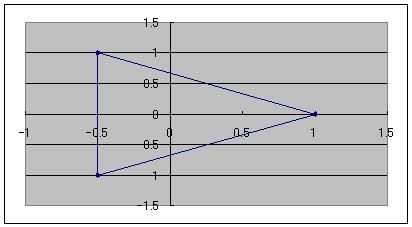 たとえばこんな三角形をグラフに書いたとしますよ。 それで、この3点をランダムに動かすとします。  そうするとこんな感じで記述する感じになりますよね、普通は。 三角+ランド() 3点のx、yそれぞれにrand()関数を足して、delボタン押しっぱなしで再計算すればいいっすよね  でもこれだとランダム幅をどんなに変えても、この辺界隈をうろついてるウゴツール的な感じを抜け出せないんですよ ブラウン運動には程遠いじゃないですか! そりゃあブラ云々道させようと思ったらできないことはないですよ!  こんな風に見たいコマ別に表とグラフを作って、視点を次々動かせばいいですからねえ できないことはないです。 けど!けど! それじゃ容量食うじゃないですか!ちょっとだけですけど! でもそんなのやっぱ嫌じゃないですかヒトとして、ホモ・菜p園スとして! そこで循環参照の出番っすよ!  三角+ご自身+ランド() これでOKっす! たったこれだけっす!  ほら、いつまでもどこまでもうろつけるじゃないですか! 循環参照はプログラムでいうfor文、つまり繰り返し命令のようなものなんす 行は縦、列は横、シートは奥行きって感じで空間的には繰り返しなんですけど 循環参照は時間的に繰り返しなんすよ そしてこの時間には空間のような制限はないんす つまり、この宇宙はエクセルでシミュられてたんですよ!!!!1 ====== ところで、宇宙が有限なのに果てがないっていうの 空間的には合わせ鏡とか万華鏡とかで理解できそうですけど 時間が有限なのに果てがないってどうやって理解すればいいんすかね? それホントに有限なんすかェ・・・? もし無限だったら・・・ただ事じゃおかねえっすよね! そんなのってあるんすか! 数学はさておき物理の世界に限って無限って!!1 ホントは無限が出てこないように宇宙に含まれるエネルギーが限られてたりするべきなんじゃないんすか!? ダークマターも!ダークエネルギーも! 幻なんじゃ ないんすか!! 実は我々は宇宙の3%しかわかってなかったんだよ って、具体的な数値でマニフェスって、人類をちっぽけに見せようとするインペーくんとコーサくんなんじゃ ないんすかーーー!!1 ナンチャッテ 宇宙・・・それは、無限のコズミックエナry  にほんブログ村
光さえも吸い込む“ブラックホール”の作り方
重力を計測する精度が向上していった未来の話 あれ?微妙に逆3乗比例でもないなぁ これ「空間」の4次元(時空合わせると5次元)にしてはちょっと小さいよね? 3よりちょい大きくて 3.5より小さくて 3.1くらいかな? もうちょいデカいな 3.15かな?いやそれだとちょいデカすぎる 3.14くらいか : : : 1週間後 どうも3.14159265次元くらいっぽい 整数でも分数でもなかった 無理数っぽいけど超越数っぽかったorz : : : 1年後 : : : いやでもまだちょっと違う 3.14159265・・・にi2.718・・・を足してみよう あ、これっぽい、これっぽいぞ! 実数ですらなかったorz ======== 補足 点とみなせる物体からの重力が物体からの距離の2乗に反比例するのは、 重力が四方八方に平等で放射状に広がっているからで、 その空間が3次元であることから、物体から出る磁力線や電気力戦同様、物体から出る重力線?の数を球の表面積で割ってるからなんです。球の表面積は4πr^2でしたよね。半径の2乗に比例でした。 じゃあもし測定で、距離の3乗に反比例したら? だとしたら意外にも空間だけで4次元あることになります。 膜宇宙理論では重力だけが3次元超の次元に染み出している可能性を示唆しており そうすると物体に近づけば近づくほど距離の2乗超に反比例して強くなるので、 ブラックホールは意外とできるかもしれない、と期待されているわけです。 じゃあどうしてすでに、重力が距離の2乗に反比例しないで観測されているのかといいますと どうも次元がコンパクト化されてちっちゃくなっているようで、距離の2乗に反比例するのは物体のごく近辺に限るとされているのです。 でも、次元が整数であるとは限らないかもしれないので じゃあ分数かな?いや無理数かな?いや超越数かな?それとも複素数かな? と考えていくと、π+ie次元とかだったら面白そうだなぁと思ったわけです。 π≒3.142 e≒2.718 実は、球を3次元以外に拡張した概念がありまして、それを一般に超球と呼んでいるのですが 超球の体積?みたいなのと表面積?みたいなのの算出方法も試算されていまして 次元の数が整数とも分数とも無理数とも実数とも限らないんだそうです。 ※ただし、負の整数ではないみたいです。 超球については過去日記参照:超球シリーズ~完結編?~(おまけつき) といいますのも、この超球の表面積の計算に階乗を用いるのですが この階乗が実は負の整数以外の全複素数で定義できることがわかっているのです。 階乗を整数から複素数に拡張した関数をガンマ関数と呼んでいます。 ===== ぼやき あ、そういや、エクセルで複素数を扱えるアドインを得たんだったな ガンマ関数の定義や級数も追加されたみたいだし このアドインでなんとか複素ガンマ関数を作るマクロが簡単に作れるようになってくれないだろうかぁ~ そういや、4次元時空とは言いながらも時間だけ別格だったら 1次元の時間における重力は時間の(1-1)乗だから・・・変化しない?とかそういう考え方はアリ? いやでも変化してるよね 万有引力定数が今も変化してるかはいいとしても、宇宙の初期の相転移ががっぽがっぽおきてたときには重力って減ってたんじゃ・・・あれ?でも余剰次元に逃げてるから減ってるように見えてるだけなのか? ってかやっぱ1次元ってハブられてる感あるよなぁ もしかして1次元だと一方通行が義務付けられるの?時間みたいに 参照: 巡回セールスマン問題と「1次元っぽさ」 1次元と2次元の間に潜んでるかもしれない深い溝のようなもの・・・  にほんブログ村
「ワイヤレス充電」って、どんな仕組みなの?
↓↓ワイヤレスが当たり前すぎる感じになったらイカのような感じなんじゃないかなあSS↓↓ 未来人1「おい2、昔は声をかけられた側もエネルギーロスしたって噂、信じるか?」 2「あれだろ、まだ電波じゃなくて音波で会話してたころの話だろ。wikiの古文書で見たことあるわ」 1「そうはいっても当時から電波での会話はやってたらしいよ。電波で音波を飛ばす方式だったけどね、これがまた面白いんだ。会話とエネルギー補給を別々にやってたんだってさ」 2「へぇ~昔の人ってそんなことしてたのか~。」 1「声をかけた側もかけられた側もエネルギーがどっかに飛んでいってたらしいw」 2「なにそれウケるw」 1「しかも当時は俺たちに数字以外の名前もつけられてたらしい」 2「まじで!?まじありえねぇんすけどw人の名前くらい番号で管理しとけよwww」 1「それとな、当時の世の中は2次元以上だったんだってさ!」 2「うそー!?時代によって次元が変わるんか!?どんな世界に住んでたんだよ昔の人は・・・うわあ・・・古文書にちゃんと書いてあるわ・・・「エネルギーの補給にはまだケーブルを用いていたところもあり、ケーブルが絡まるという現象も存在した」・・・「絡まる」って、なんだ?」 1「や、それがな、2次元だと「回り込む」って現象が、2次元よりもさらに上の次元、3次元空間だと「絡まる」とか「またぐ」とかいう現象が発生したらしいんだよ!」 2「なんだそりゃ!?イメージしづれえなあ」 1「テンソル使えばイメージしやすいんじゃね?」 2「テンソル?・・・添え字3つつけて多次元配列にしてみるわ。ああ~なんとなくわかった。でもさ、昔の俺たちが3次元の世界に住んでたんなら、じゃあ今のこの世の中ってホントは1次元じゃないんじゃね?昔3次元で今1次元だったらいつから次元低下したのよ?連続的に?それとも不連続的に?」 1「・・・あ、そういえば・・・これはちょっと怖い話だな・・・!投稿したらホラー物理学賞取れるかもしれない」 2「でもその話ホントにあてになるの?直接確かめたほうがいいんじゃない?」 1「ちょっと見に行ってくるか。そういう世の中があったかどうかを確かめればいいんだよな。個数が厳密にゼロじゃなかったらいいんだよな。今検索かけてる。」 1「・・・あった」 2「まじで!?スゲー!!」 1「しかも・・・たくさん・・・」 2「ェ・・・」 1「1次元だと思ってる俺らのほうが少数派らしい・・・」 2「オオォ・・・」 1「しかも、3次元じゃなくて約3.14次元って言ってる世界線もあった・・・」 2「円周率かよ!無理数かよ!」 1「あ・・・約3.14+i次元って言ってる世界線まで・・・」 2「次元の数が複素数かよ!!超越数+虚数かよ!!わっけわかんねー!」 314159265 ガロアとガウスとガンマ関数はなんとなく似ている ガンマ関数億π  にほんブログ村
僕の趣味は大きく分けて3つある。
電子工作とプログラミングとエクセル。 今日の日記では、今後の僕の趣味のあり方について考える。 ======= 僕の部屋には大量のガラクタがある。 父はもっとガラクタを保有しているので、遺伝的要素は強いと考えられる。 僕は自分が、リアルの物体の管理が苦手なのを知っているつもりだ。 電気工学やPCの経験から、僕が管理に特化しているのは一次元のデータなのではないかという仮説がある。 PC内のデータは一次元に還元できるので、管理は容易 紙のデータ管理は煩雑。重さがあるのもあるが、2次元以上であることが主な原因と考えられ 縦と横の比率の違う紙が混在するとイライラして管理したくなくなる。 その上、書いたデータが文字や描画部品ではなく ただの再利用不能な図形データとして保存されるのも許せず 紙がめくりやすかったりめくりづらかったりするのも絶対に許せない。 限りなく2次元に近い3次元物体である紙ですらこうなのだから モロに3次元の物体をイカに管理しづらい性格なのかはご理解いただけたと思う。 3次元物体になってくるとホコリもかぶるし、こうなると片付けたいのにアレルギーのせいで片付けられない(あるいはそれを言い訳にしていつまでも片付けない)などという状況が発生する。 電子工作も結局は2次元以上の物体だ。 少なくとも低周波の回路は限りなく1次元に近い2次元の図面で書き表されるが 機械的回路系になるとどうしても3次元的な要素が加わってしまうし 結局電子部品でも部品自体が2次元以上の物体なので、その管理に結構困ってしまうのだ。 この困難を乗り切って成長できれば、趣味としての電子工作はだいぶ成長できると思うんだけど 成長できなければ部屋に溜まったガラクタは一生負の遺産として残り続け リサイクル関係なんかで、いつかはその負の値段が高騰する日も来るかもしれない。 そう考えると、電子工作の趣味を持ち続けるべきかというのは大いに悩みの種で 他の趣味だってまだまだあるんだからそれで一生楽しめるんじゃないの? と言われれば「きっとそうだろう!!」とか即答できそうだったりする。 つまり電子工作の趣味は諦めたほうが得策なんじゃないかと。 ======= 次に、プログラミングの趣味。 プログラミングには何度となく魅力を感じながらも、実際に組んでみて何度と泣く泣かされてきた。 ICもそうなんだが、僕は唯一無二の自然法則が大好きだったりする。 っていうかそれ以外が大嫌いだったりする。 (その割には自然法則を変えたいとか思ったりもするんだけど。) 人間の決めた約束事なんて滅んでしまえって思うときもよくある。 だから僕はオブジェクト指向には向いていない。 そういう約束事を設計して積み上げていくのに向いてないんだ。 別に僕だけとも思わない。人間全体がオブジェクト指向に向かない可能性だってあると思っている。 ただ、もしそこを乗り越えて自分のものにできたとしたら、ものすごく成長できると思うんだけど 成長できなければフォルダに溜まったいくつものプログラミング言語の開発環境は一生負の遺産として残り続け PCのデータが飛んだりして、いつかはその負の値段が高騰する日も来るかもしれない。 そう考えると、プログラミングの趣味を持ち続けるべきかというのは大いに悩みの種で 他の趣味だってまだまだあるんだからそれで一生楽しめるんじゃないの? と言われれば「きっとそうだろう!!」とか即答できそうだったりする。 つまりプログラミングの趣味は諦めたほうが得策なんじゃないかと。 ======= じゃあ何が残っているのかというと、エクセルだけは毎日いじっていて楽しい。 マクロも最低限コピペで組めたりするけど なるべくマクロには頼らない生活を送っている。 バグが不可視気味になるのが嫌なんだ。 そういう意味ではやはり低次元的な脳なんだな僕の脳は。 せいぜい、行と列と、おまけでシートの「にわか3次元」程度しか配列がないのだろう。 それでも、一生遊べるだけのフロンティア的なポテンシャルはエクセルは持っていると考えているし それを引き出せるだけのものを自分も持っていると考えている。 そういや、エクセルの開発者は複数人いるはずだから その1人1人が各分野のプロだとしても、エクセル全体のプロが地球上に1人いるかどうかってなったらそれは別問題なはずだよな。 マクロをコピペし、アドオンをDLしてアドゥィーンして何かテーマを持って遊んでいれば 低コストで毎日楽しく老後まで暮らせるんじゃないかと そう思っている。 ただ、何らかの病魔に頭が真っ先に犯されて、 足し算すらままならないボーっとした状態で生きてるのか死んでるのかもよくわかんないのがしばらく続くのは嫌だな それくらいなら手足とかで脳や人生のゴールを買うわ。 ======= リアルでもPC内の世界でも、やっぱり見える化ってのは大事だと思う。 資産を捨ててでも、見える化しているだけでそれ自体が資産になると思っている。 余計な趣味はやっぱ・・・切り捨てようかなぁ、うーん 人生100年で、電子工作・プログラミング・エクセルにそれぞれ100年ずつ遊ぶ余裕があったら エクセルだけで太く短く100年遊んだほうが得なんじゃないかとはかーなーり思うわけです、はい。 それが、電子工学を学んで結局バイトで生計を立てている一個人の学業の楽しみ方なんじゃないかなぁと。 もう30歳だし、趣味の方向性くらいそろそろ決めたっていいんじゃないの。 踏ん切りだけがまだついてないんだけどね。w  にほんブログ村
たぶん価値っていうのは上下関係がはっきりしていて、しかも上下をさかさまにすると成り立たないものだと思うんです。
たとえば量子論の行列力学に出てくるヒルベルト空間を使ってあらゆる多様性の直交関係を計算するところから始めるとか。たとえば「無矛盾(正義)」と「矛盾(悪)」。無矛盾は矛盾しないので存続できるのに対し、矛盾はすぐに自己矛盾で自滅してしまうように、さかさまにはできないと思うのです。 ところが多様性というのは平面の中の点のようなもので 位置の違いはあれど、それの大小を比べる術がないようなものだと思うのです 喜怒哀楽の喜と哀が横軸、怒と楽が縦軸みたいな感じで。 その軸が2つだけじゃなくいっぱいあるんですよ 喜と哀だけだったら喜しか残らず、怒と楽だけだったら楽しか残らないのに、組み合わせただけで両方存続できちゃうんじゃないかと思うわけです。 ただ、位置の違いを「距離」という価値めいたもので測ることは可能で、 それが「価値観の差」となってピタゴラスの定理で具体的に良し悪しとして出てきてしまうことがあると思うのです。 平面や立体などとして組み合わせなくても、単体でさかさまにできるモノたちもあるかもしれません。 黒いものほど好きっていうのと白いものほど好きっていう感じでしょうか。 分類としては以下のようになると思います ・単体でさかさまにできるもの(最高と最低が最初からありえません) ・単体でさかさまにできないもの(最高と最低がありえます) ・さかさまにできるものの複合体 ・さかさまにできないものの複合体(もはやレベル付けができません) ・さかさまにできるものとできないものの複合体(同上) この世の中がこのうちの5つ目だけからできているとしても、十分複雑な状態になりえると思います。しかもそこから「価値」という上下関係のはっきりしたものを抽出可能なんだと思います。 でもあくまでそのはっきりした上下関係は「おまけ」であることを認識しないといけないと思っています。 人間や生物のいない自然界は割とスッキリしている合理的なシステムだとは思うのですが 人間や生物がこのスッキリした糸を絡めてしまったのでどんどん絡まっていっているのだと思います。 ただ今後、人間や生物がこの絡まった糸を芋づる式に解いてスッキリした自然界に近い状況でかつ、文明を保つことは決して不可能ではないどころか、アプローチしだいではすぐ近くにまで迫っている可能性もあると考えているのです。  にほんブログ村
巡回セールスマン問題とはどういうものなのか
僕が以前、新聞配達のバイトをしていたときに思ったことがあるんだけど 新聞配達員問題と名づけてもいいくらい、同じような問題に直面する。 順路の問題 横に長い区域の担当だったとする そこでは、僕はその横に長い区域を、縦にぶつ切りにしていって その1つ1つの縦の区域ごとに時計回りに配る順路にしていた 左端のぶつ切りから始めて、1個ずつ右にシフトしていく。 (ストークスの定理とか、土鍋部分に邪魔されたIHクッキングヒーターのうず電流をイメージできる人はそれがいいと思う) そうすると、問題が生じる 1個目のぶつ切りの帰り道(下向き)と、2個目のぶつ切りの行きの道(上向き)がカブるわけだ。 これじゃ効率がよくない と思って、今度は担当区域を横にスライスした。 時計回りに配るのは同じだけども 横にスライスすると、スライスの上から順に下にシフトしていくことになる やっぱり、1個目のスライスの帰り(左向き)と2個目のスライスの行き(右向き)がカブる。 結局効率の悪さは似たり寄ったりなのではないか。 ただし、碁盤の目に満遍なく家があって人が住んでいるとは限らない。 どうすれば効率よく回れる? ↓ めんどくさ! ↓ 順路考えたヤツ、good job! ものすごく大雑把にいうと、これが「巡回セールスマン問題の根っこ」だ。 今度は、その建物が全部3階建てのアパートだったと考えよう どうなるか? アパートはA棟、B棟、C棟、D棟と分かれているのだけど 管理人が割とおせっかいな人で、全部ではないがあちこちに渡り廊下を準備してくれている。渡り廊下に限らず、廊下は走ってはいけないらしい。ボロいのか? 階段に亀裂が目立つ。 配達員はよけいに悩む。どの順路でいくべきか。 東西ぶつ切りか、 南北スライスか、 各階ごとか、 どれを優先して回ればいいのか、自由度が増えた分、悩みも増える。 (階段上り下りの体力のことはあとで考えることにしている) ということは、平面でも立体でも、たぶんそれ以上の次元でも、巡回セールスマン問題は存在するということだ。 じゃあ逆に、客の家が一直線上に並んでいる区域を担当したらどうなるか? ここでは問題は起きない。 販売所のすぐ近くに区域の左端があって、右端の近くに配達員の家があったら、迷うことなく左から右に一気に配達して直帰するだろう。 つまり、1次元だけは巡回セールスマン問題が発生しない。 1次元は特別な次元なのだろう。 次に、1次元っぽい2次元を考える。 家が直線状に並んでいるのは同じだが、2行に配置されている場合だ。 この場合は、1次元ほどではないが、割と簡単だろう。 北のスライスを西から東に進んで 東端についたら、折り返して南側のスライスを東から西に進めばいい。 あまり悩むこともない。 逆にいうと、家が「真四角の中に並んでいる場合」のときは大いに悩む。 これは何を意味するのか? 同じ2次元でも、1次元っぽさの違いによって、問題の難易度が違うということだ。 この難易度は、四角形の外周と面積の比によるのではないか? カタチを四角形に限定すると、同じ外周で面積が一番でかいのは真四角だ。 紐で作った輪っかを目いっぱい広げようとすると真四角に近くなるだろう。 逆に、一番大きいのは、限りなく線に近い面(細長い長方形)だ。 面積がほとんどないので、外周/面積の比は限りなく大きい。 この量を「1次元っぽさ」と呼ぶことにしよう 1次元っぽさの定義 辺の長さが1cmの真四角でいうと、外周の4cmを面積の1cm2(平方センチメートル)で割った、4といった感じの量。長さの逆数の次元を持ち、 単位は[(cm)^-1]などと表記する。 同じ外周で、棒状になったら限りなく大きくなる、カタチによって変わる量 超球状に配置されていたら、その領域の表面積めいたものを体積めいたもので割った量。 巡回セールスマン問題はこの「1次元っぽさ」が小さいほど難しくなるのではないか。 単位の表現がこめんどくさいので、いっそのこと「ナントカの難易度」=「1次元っぽさの逆数」(長さの次元を持ち、単位はcmとか)にしてもいいかもしれない。 (1次元っぽさを考えていたら1次元なのに単位が長さの逆数で混乱した) なーんてことはきっともう誰かが提言してるんだろうなー^^って話 これが超時空サッカーだ! イナズマ・フロンティア  にほんブログ村
シュタインズゲート
ゲートキーパーズ スターゲイト ナノセイバー など なんかこう、ひきつけられるものを感じ気を感じるんだ。 タイトルについてるだけで、期待感3割り増し?みたいな たぶん、異世界にいく方法を割りとガチで探していたからっていうのもあると思うんだけど その辺みんなはどうなんだろう? それと、最近の魔方陣って発動する人との位置関係や向きなんかはさておき なんかみんな似たような感じだよね。 前に出たり下に出たり、後ろに出たり、横は・・・ないみたいだけど たとえば ストライクウィッチーズ オカルト学院 DOGDAYS などなど あれのデザイン的な元祖は誰なんだろう? もしかしてゲートキーパーズの人? でも、こういう平面的なゲートっていうのは 我々が3次元空間に住んでいることの象徴のような気がする。 たぶん、4次元の空間に住んでいたら、1つ次元を落として3次元の魔方陣を描いていたんじゃないかなぁと。 まあ、4次元の住民が2次元の魔方陣を描く可能性も否定できないけどね ただ、1次元だと魔方陣そのものが描けないから、 4次元の住民は自由度が多くてうらやましいですなぁ ただ、3次元の空間で2次元のゲートっていうのはホントなら不自然なんだよな いわゆる「どこでもドア」を例にしてみると のび太の家でドアを横からつぶそうとしたら、行き先のほうではどうなるのかとか 行き先を変更したら、ドアはどんな風に消えたり現れたりするのか また、現れる最中のドアの場所に人が立ってたらどうなるのかとか ドアを2回くぐったらのび太の部屋に戻るのかとか 違和感はみんな感じてると思うんだけどね。 物理でようやく、ゲートめいたもののあり方を議論できるようになって ゲートっていうのは平面的(2次元)なものじゃなく、星のような塊(3次元)であるべきってこともわかってきてるみたいで。 要はブラックホールみたいなもんさ。 天体であると同時に穴でもあるわけ。 こう考えると、どの方向から見ても同じようにゲートに見えるから、違和感は少ないんじゃないかなぁみたいな。 でも、ブラックホールが回転してたら、やっぱり2次元の穴もあるっぽいんだけどねー 外側に3次元の穴(イベントホライゾン)があって、内側に2次元の穴(リングになった特異点)がある。 特に内側の穴をくぐったらどうなるのかは今のところ誰もわからない。 そもそも、その内側の穴っていうのは点であるべきとされていたのに、どういうわけか輪っかの状態にもなるって時点で困惑しているわけだし。 シュタインズゲートのクリス(ティーナ)が言ってるカーブラックホール(回転するブラックホール)のことなんだけどね カーブブラックホールとは言いえて妙だな。 大気中でまわしたらブラックホールのまきゅっができるかもしれんんんんn にほんブログ村
なんてこなたい。確か先生がいたはずだ。ドイツ語の先生じゃなくてな。
でも、これ見てみろよ。ドイツ語の文法。 わざわざwikipediaにしてまとめてあるってのもびっくりしたけど 昔ドイツ語習わされたことがあってな、第2外国語として。 変数がいくつもあるんだ。 性・数・称・格 って。ノートで1つの表にまとめようとしたらまず紙面をはみ出した。 ってことは3次元以上の配列ってことだよ 実は4次元配列だったとはよ・・・orz 4変数関数と言ってもいい。そうすると5次元以上になるな・・・関数の戻り値が1つだけとも限らん そんなん、理系でもめったに使うやついないって・・・せいぜい2次元配列化した行列程度だろ・・・ だからドイツ語圏の人は母国語の文法が嫌いなんじゃん・・・ なんだ、カルノー図使って無理やりやるか!?やだよ ドイツ語は、つづりと発音がキッチリしたアルファベットもどきだけで十分です。^^英語でおk にほんブログ村
もしかしてそれは・・・実在するかしないかというものではないだろうか・・・
かねてから、 「一次元の住民は無理数の概念に気づくことができないのではないか」 (※厳密な1次元空間に生命体が住んでいるわけではなく、前後移動しかできないために1次元しか認識していない生命体のこと。 面積や体積の概念がないので2乗や3乗をしたことがない上、斜めという概念もないため、ピタゴラス(三平方)の定理がイメージできず、円の概念もないため円周率πがわからず、関数をイメージできないため自然対数の底であるeのイメージもわかず、当然複素数の概念もわからない) という奇妙な仮説が頭から離れないのであるが、 (過去日記参照) これがパラドックスだったらどうなるだろうか 「前提が間違っている。一次元という概念自体が破綻していたのである」 とかなんとか。 複素数と比較した実数という集合は、欠けた存在であると表現されることがある。 また、複素数は要素が2つしかないのにすでに欠けていない存在であるとも言われ、 さらに、要素が2つの複素数からは、要素が4つや8つの四元数(クォータニオン)や八元数(オクトニオン)といった概念も派生が可能であるらしい。 一次元の量は大きさを持つが、2次元以上になると大きさという概念が消えるということもよく言われる。 ということは、実在可能な次元というのが実は1次元からではなく2次元以上だったということはありえないだろうか!? だからこそ、2次元以上の住人は無理数を考えることができるが、1次元の住人は考えることができないなどという奇妙な結論が導かれるのではなかろうか!? そんなホラーなコメディ・エンターテインメントはいかが? 関連日記 HS:いつか宇宙の究極理論ができて FU:超球シリーズ~完結編?~(おまけつき) にほんブログ村 |
カレンダー
カテゴリー
最新CM
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
[03/17 Robertaverm]
最新記事
(01/01)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
(08/04)
(10/24)
(06/08)
(05/22)
(01/13)
(11/04)
(11/02)
(10/28)
(10/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
43
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|