UBD：重力反比例。あれ？2乗じゃねえなSS～リカバリ～

重力を計測する精度が向上していった未来の話


「あれ？重力が反比例するのって距離の2乗と若干違う。」

　「え、まじ？そうなの？」

「何乗ぐらい？」

　「2乗超、3乗未満」

「曖昧だなぁー」

　「だって精度悪いんだもん」
：
：
：
1週間後
：
：
：
「2.14乗ぐらいだわ」

　「何が？」

「重力反比例。」

　「えっ！？整数じゃないの！？」

「なんかねー。てか2超3未満って言った時点でツッコんでほしかった･･･」

　「あ、そういえばなんで逆2乗なんだっけ？」

「あれでしょ、空間が3次元だからでしょ」

　「あれそういう理由だったの？」

「子供んときやったじゃん。1テラ㌧の点重荷から出る重力線の数は合計で1本。
全方向に放射状に出るから、じゃあ点重荷から1インチキメンタル離れた球体の表面積で割ったら逆2乗則が理解できるよねって。」

　「あーあったなー！そういや、重荷が線上の線重荷から出る重力磁場の磁力線の本数は2次元空間で考えるから、逆1乗法則だったんだっけな」

「そうそう。だから今週は球体の表面積を測ってみました。」

　「そっちからきたかー！」

「半径1インチキセンチメンタルの球の表面積は、12.6ではなく13.5平方インキチメンタルくらいだったのです！」

　「ｼﾞｬ･･･ｼﾞｬﾝｼﾞｬｶｼﾞｬｰﾝ！4πよりちょいでけえ！･･･ん？次元数って整数じゃないの？」

「3.14次元だったりしてなｗｗ」

　「円周率ｗｗｗそれより、小数次元の球の表面積なんて、理論値あったのかよー」

「n次元の球を超球とか呼ぶらしい。そんでその超球の表面積SってのがS=2π^(n/2)*r^(n-1)/Γ(n/2)なんだってさ」

　「なんだよそのΓとかってヤツ。key()？」

「ガンマ関数ってヤツで、階乗の親戚だってさ。たとえば4の階乗って4!(ビックリヨン)って書いて、4・3・2・1って1になるまで全部掛け算するっしょ？」

　「ああ、総和∑の掛け算バージョンみたいなアレか！」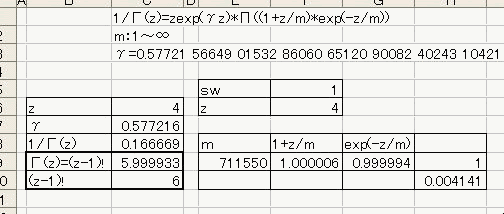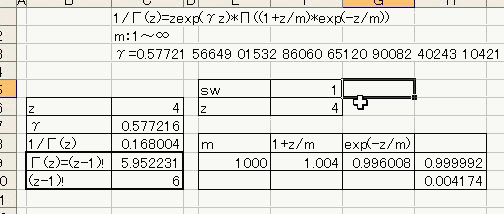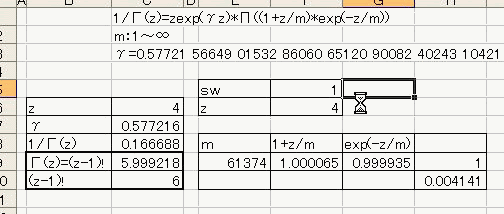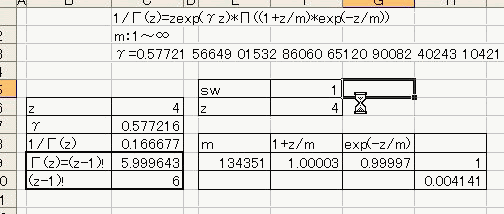




「あれ実は、実数に拡張可能らしいｗ」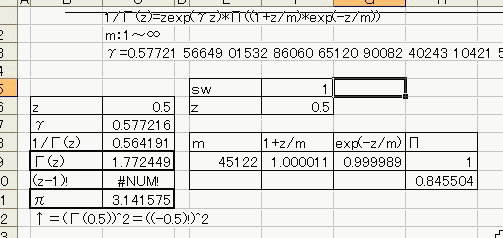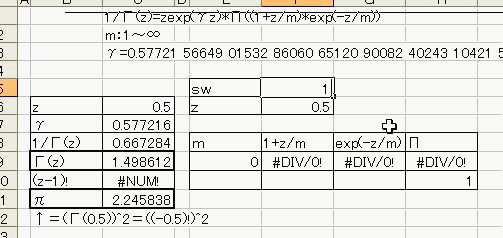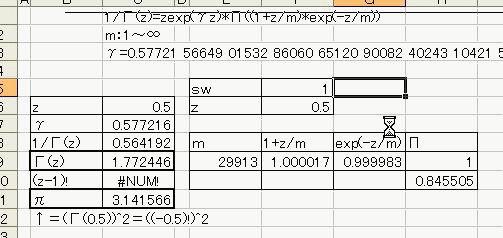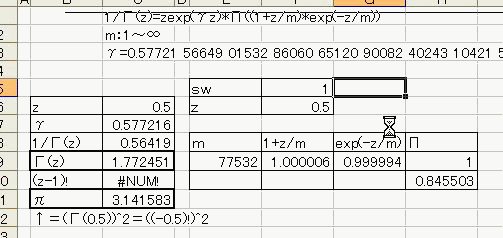

　「まじでｗ」

「しかも、階乗が実数に拡張可能だったら、超球の次元数を整数に留める道理も特にないらしいｗｗ」

　「えええｗ」

「※ただし、負の整数は除く」

　「なんで負の整数だけハブられてんのｗｗｗ」

「だって、(-1)・(-2)･･･って掛け算してったら発散しちゃうじゃん」

　「さすが数学ｗｗｗ常に斜め前を行っててわけわかんねーのに筋だけは通ってるｗｗｗ」

「ま、ガンマ関数を階乗に翻訳して簡単に書けば、n次元空間の超球の表面積Sは、S=2*π^(n/2)/((n/2-1)!)で書けるってことらしいよｗ」

：
：
：
1週間後
：
：
：
　「ちょ、大変なことがわかった。」

「どうした？」

　「ガンマ関数の中身は実数に留まってなかった！」

「ぶー∴(ﾟεﾟ )ｗｗｗなにそのタイムリーｗｗｗ」

　「どうかしたのか？」

「俺も似たようなこと考えてたんだよｗｗπのn/2乗のnが複素数だったらどうなるのかなーってｗ」

　「やってみるか！」

「なにを？」

　「ほら、先週の球の表面積、円周率約3.14次元にしてはなんか引っかかったじゃん。」

「ああーあれね。･･･もしかして誤差じゃないってことか！？」

　「もしよ？π+i/e次元だったら！？」

「3.14云々＋i0.368云々次元ってことかー！」

　「ほら、少なくとも表面積の実数部分は13.512でピッタリ。」

「ｷﾞｬｱｱｱ俺たちって無理複素数次元人だったのかよ！」



＝＝＝＝＝＝＝
補足：
循環参照にまだ慣れていないせいか、複素数まで拡張したガンマ関数の値がおかしいようです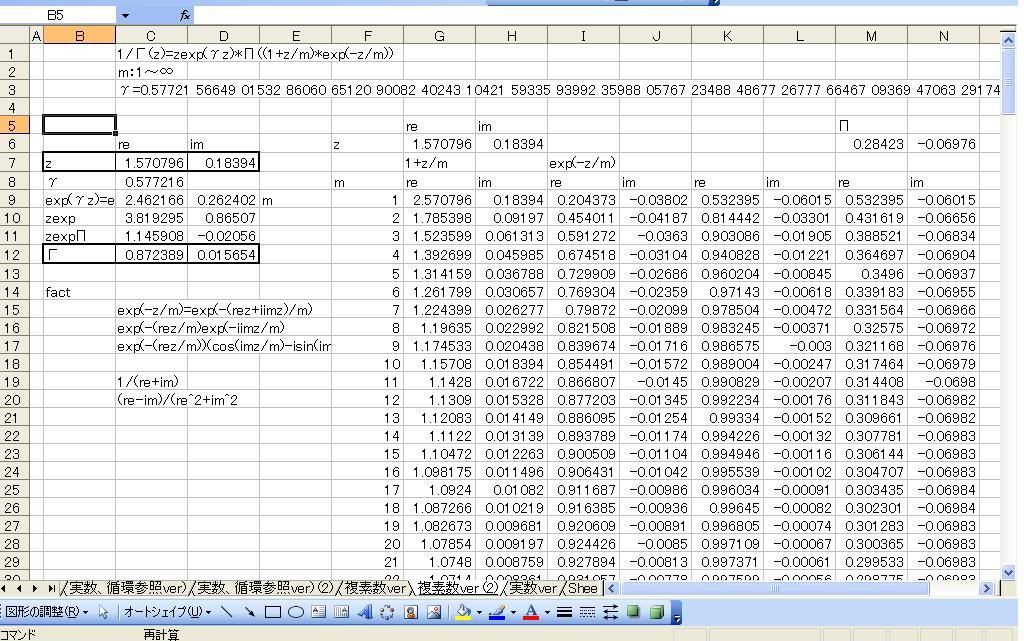

循環参照しないとだいたいうまく計算できるようです。google電卓参照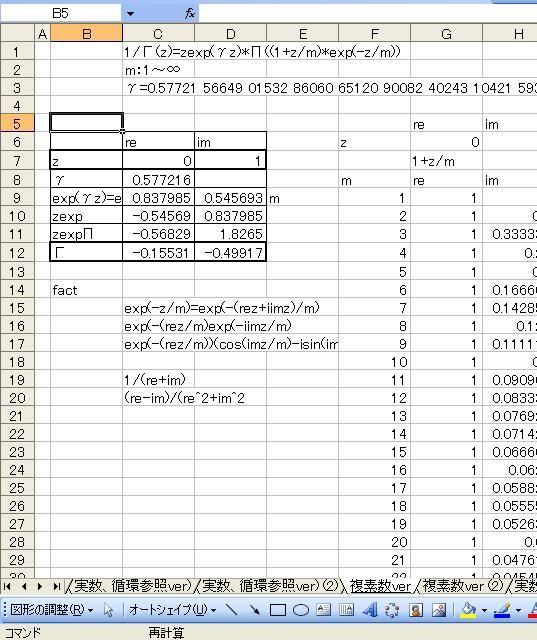


だいたい、といったのは、循環参照してないほうで、虚数単位のガンマ関数Γ(i)を計算してみたところ
google電卓の結果と比較して、なぜか実部と虚部とか符号が逆転するのです。
僕の計算にバグがあるのか、wikiかgoogle電卓のほうなのか
なんともいえないです。
wikiの3Dグラフは絶対値しか表示してないので、実部と虚部の入れ替わりや符号の参考には使えませんでした

なんとなく逆数と勘違いしてるとかその辺のミスだとは思うのですが、ワイエルシュトラスの乗積表示とはつい最近出合ったばかりなので、いまのところ確認の方法が見当たらないです＞＜


ただ･･･、π+i/e次元のガンマ関数は結果的にはだいたい合ってるみたいです＾；





にほんブログ村