希望的観測日記　ブログ枝部（偶関数＆奇関数）×偶関数・奇関数・(偶関数＆奇関数)

20080511～ 13と7と11の倍数の論理積は13と7と11の積の倍数である。和ァ・・・

[2933] [2932] [2931] [2930] [2929] [2928] [2927] [2926] [2925] [2924] [2923]

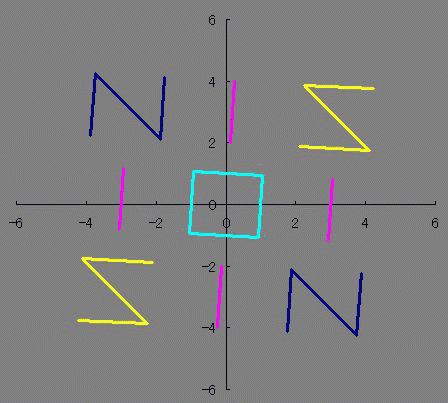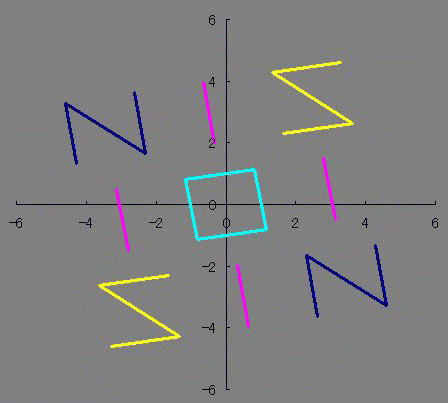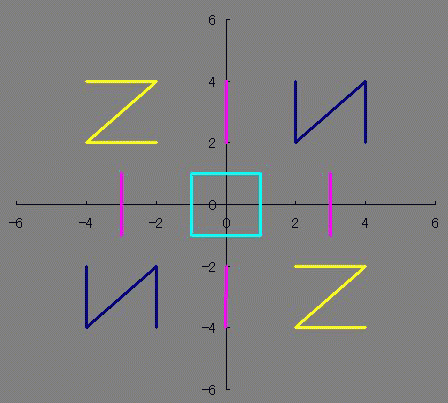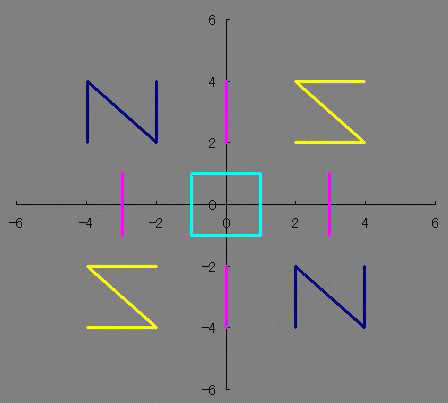整数は必ず偶数か奇数に分類されるのに
関数は必ずしも偶関数か奇関数に分類されるわけじゃないですよね

どちらでもない関数もあれば、
どちらでもある関数もあります

たとえばy=0は偶関数でも奇関数でもありますが
他にも有るんじゃないだろうかと、条件を整理してみますと
ただ単にx(横)軸対称でありさえすれば偶関数でも奇関数でもあるということがわかります。

NIS
IOI
SIN　西尾維新

さんは惜しかったね！

楕円とか双曲線とかがそうですね

あんまり話題にされないのかな？
偶関数でも奇関数でも「ない」関数のほうが話題になってる気がします

ググる際に「楕円関数≠楕円の関数」と「双曲線関数≒≠双曲線の関数」
というネーミングも邪魔をしているのでしょうか

ところで
偶関数×偶関数や偶関数×奇関数、奇関数×奇関数が楕円や双曲線でどのようになっているのだろうと気になりまして
実際に掛け算してみました。

楕円の式は

双曲線の式は

ですが、2種類の双曲線のうち今回使いたいのはy軸対称ではなくx軸対称のほうなので
(x/a)^2-(y/b)^2=1のみ使います

y=±b√(±(1-(x/a)^2))

のうち、1つ目の複合はx軸対称であるために重要なものですが

2つ目の複合は後述しますがぶっちゃけ必要ありません
プラスだったら楕円、マイナスだったら双曲線です。

楕円×楕円をやってみましょう。究極の同性愛です。
2つの楕円でa、bが異なるとします。

y1=±b1√(1-(x/a1)^2))

のy1×y2をやってみましょう。

y=y1×y2
±b1b2√(1+(x^2/a1/a2)^2-x^2(1/a1^2+1/a2^2))

になると思います。

次に、双曲線×双曲線をやってみましょう。
これも、楕円×楕円と同じ結果
y=±b1b2√(1+(x^2/a1/a2)^2-x^2(1/a1^2+1/a2^2))

になることがわかるかと思います。

グラフはこんな感じです。

（偶関数＆奇関数）×（偶関数＆奇関数）は、やっぱり偶関数＆奇関数の両性具有だということが判明しました。百合×百合＝ホモ×ホモ＝ふたなり　だったというわけです。
しかもシスコン・ブラコンの属性も有ることがわかりましたね！とんだ変態でした。

楕円×双曲線はどうでしょうか

これは実数にはなりません

双曲線は楕円の外側にしか値を持っていないので、掛け算するとどうあがいても値を持てないのです。
だから2つ目の複合±は意識しなくても良いということなんです。＋×＋＝－×－になって、＋×－が存在しないわけですからね

しかしながら、楕円×楕円と双曲線×双曲線がイコールで結ばれたことはちょっとした驚きですね

一度数値として出力してから掛け算してたら気づかなかったかもしれないところです。
ビバ解析計算！

それにしてもファインマン・ダイアグラムに見えて仕方がないです
まあExcelだと「空白ではない非数値」をゼロと描写してしまうからなんですが。

（偶関数＆奇関数）×偶関数
や
（偶関数＆奇関数）×奇関数

はどうなるでしょうか

結果はこれらもまた（偶関数＆奇関数）に収束してしまいます。

y=0になにかけてもy=0になるのと辻褄が合いますね。関数ホイホイというわけです。人類ふたなり化計画のようですね