ZAD：コ サインはＶ(単位はボルト)

ちょっと古い話




おととしくらいに、コサインボルトのダジャレを具現化する方法を考えたんだ。

I(t)=Ic・cos(φ(t)-π/2)
=Ic・cos(∫V(t)dt/Φ0-π/2)

これの、I(t)に抵抗でもかましてRI=Vとかってしたらさ

(V)=cos(V)　ﾌｫｯﾌｫﾌｫｯﾌｫﾌｫｰ

みたいなヘンな式ができそうじゃんか。
これをVについて解きたかったらどうするよ？

V=√(V+1)

とかだったらな、単に両辺2乗して2次方程式解けばいいだけの話だし

cosV=a

だとしても逆関数使ってV=Acos(a)ってすればそりゃぁ解けるけど

cosV=Vは自分自身とイコールだからなぁ
2分法でも使って数値解析しないと解けないんじゃね？

つうわけで循環参照の出番キマシタヨー

＝＝＝＝＝＝＝
方法

1つ目の表
F4：循環参照開始スイッチ(オン：1、オフ：0)
F5：Vの上限初期値→1
F6：Vの下限初期値→0


2つ目の表
D列：V　上からそれぞれ上限、下限、中点
中点＝average(上限、下限)
E列：cosV→cos(D列)
F列：2分法の判定符号。V-cosVの符号。sign(V-cos(V))

循環参照部分
D9=IF(F4=0,F5,IF(F11=F9,D11,D9))：上限のsign＝中点のsignなら中点のVを採用、≠ならV上限を維持
D10=IF(F4=0,F6,IF(F11=F10,D11,D10))：下限のsign＝中点のsignなら中点のVを採用、≠ならV下限を維持
※ただし、循環参照スイッチがオンのときに限る。
循環参照がオフのときは初期値(上限、下限それぞれF5とF6)を保つ。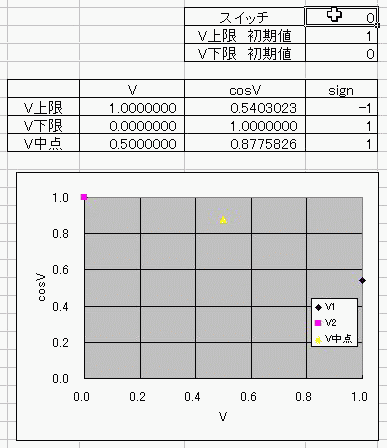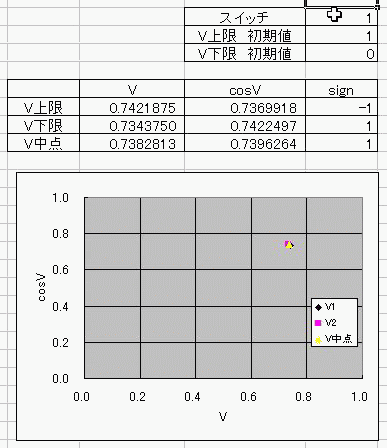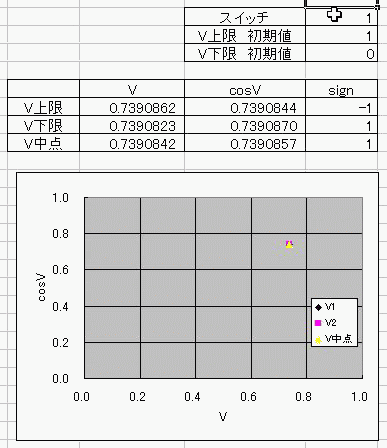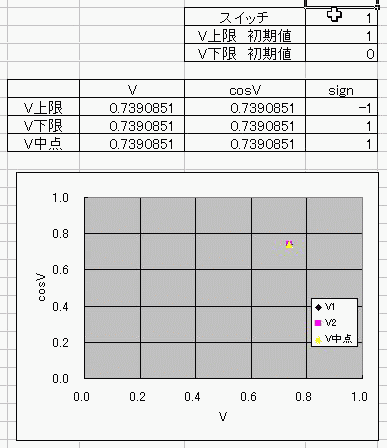



＝＝＝＝＝＝
だいたい0.74rad(42度くらい)でコサインボルトはボルトだそっすよｗ

にほんブログ村