FTC：マクローリン展開をExcelマクロでやってみない試み

高校の数学でマクローリン展開ってのを習ったじゃないですか
そんなん習ってない人のことなんて僕は習ってないんでお構いなしで話しちゃうじゃないですか


あれです、たとえば
100万円に月0.01%の利子がつくとしたら3ヶ月後にはどうなる？っていうのを計算するとしますよね

100万×1.0001^3が3ヶ月後の金額じゃないですか
1.0003を3回かけるわけです。
でも0.01%=0.0001が1に比べてはるかに小さいとき
(1+0.001)^3≒1+3・0.0001に近似できるよーって話


マクローリン展開はそんな感じの話です。
もう少し広い意味ではテイラー展開なんですけどね。


コイツがどんなところで使われているかっていうとPCの中はコレだらけです。
デジタルコンピュータのPCさんは基本的に足し算しかできないので。
四則演算だってPCさんは足し算にしてやってるんですよ。

まず引き算は「マイナスの数を足す」と解釈します。マイナスの数はプラスの数の補数で表現可能です。

次に掛け算は「足し算の集まり」と解釈してもいいですし、「桁をシフトさせる」と解釈してもいいです。
12を10倍した120は12を左にシフトさせたと考えることができます
これを10進数ではなく2進数で考えると、12→1100を2倍するには左にシフトさせて11000にしてしまえば24の完成です。

逆に24→11000を半分にしたければ右にシフトさせて、1100にすれば12に戻るので、割り算もこうすればできることになりますよね。



じゃあエクセルのサインとかコサインとかはどうやってんの？といいますと
別に全部暗記してるわけじゃないんですよ。
かといってcos15°を30度の半分なので半角の公式を使っている、というわけでもないです。

じゃあどうやっているのかといいますと、これも全部足し算に戻して計算しているわけです。
そこでマクローリン展開が必要になってくるわけです。

コサイン関数をマクローリン展開すると、ある数列が顔を出します。
これをマクローリン係数と呼ぶことにしましょう。
マクローリン係数にcos(x)の中身のx、xの何乗かをかけたものをマクローリン数列と名づけるとして
これらを全部足したものはマクローリン級数と呼ばれています。

「級数」というのは数列を足したものを言います。
たとえば1+2+3･･･+7+8+9+10=55
これも級数です。
ただし、1から10までの足し算です。

どこまでも果てしなく足したものを「無限」級数と呼びます。


マクローリン展開というのは、マクローリン係数にxの何乗をかけてマクローリン数列にし、
それらを全部足して無限級数にすることでどんな関数でも表現できるよ

というものなのです。つまり、どんな関数も足し算だけで表現可能なのです。
ただし、どこまでも足した場合です。

限られたごく一部の関数たちは3回足しただけで出来上がるのもいますが
たいていの関数は基本的にどこまでも足します。
しかしPCさんはそんな無限に立ち向かえるようなスペックを持っていないので
「途中」で足し算をやめます。
その途中までの係数を、PCさんは暗記しているわけです。

暗記といっても理解に近いかもしれません。
マクローリン係数は整数ではないものの数列なので、ある規則にのっとって変化します。
PCはその規則を覚えているといったほうがいいかもしれません。



では実際に、コサインのマクローリン展開をやってみて、エクセルのコサインと合うかどうかやってみましょう。

こういうとき、普通はプログラミングをしてマクロを組んでユーザーの定義した関数を作るのですが
僕はプログラミングが苦手なので、マクロは今回一切作りません。
どうしてプログラミングが苦手なのかというと、バグがよく見えないのです。
だから、いちいちセルに表示して確認しないと嫌なのです。

この図を見てください。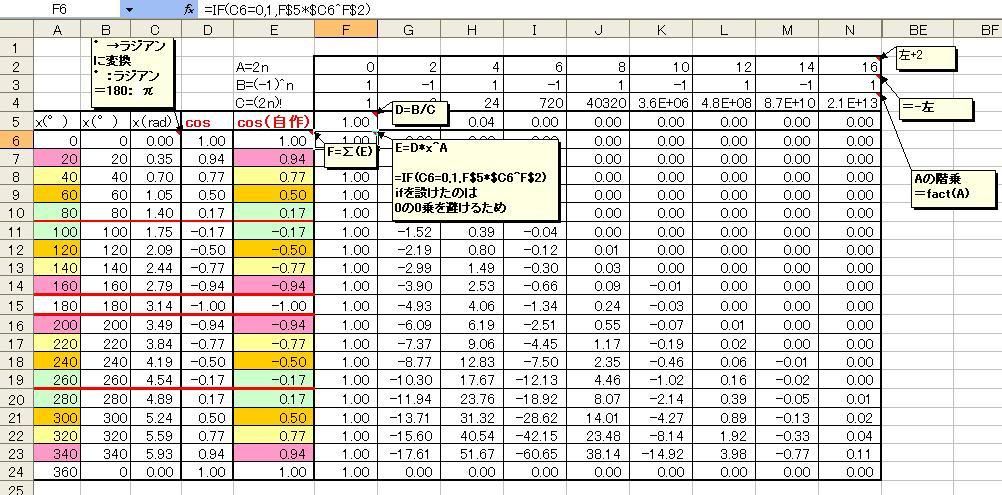

cos(x)はマクローリン展開すると

cos(x)=∑((-1)^n・x^(2n)/(2n)!)

で再現できるのですが

nを整数として
A=2n←0、2、4、6、8、10･･･などといった偶数の数列という意味です
B=(-1)^n←マイナス1のn乗、つまりプラス1とマイナス1を交互に繰り返す数列という意味です
C=A!←（「faxt(A)」や「A！」はAの階乗数列、たとえばfact(5)や5!は1・2・3・4・5を意味します）
D=B/C←マクローリン係数
E=D・x^A←マクローリン数列、そして
最終的に表現したい関数をF=∑(E)←マクローリン級数　∑(しぐま)はです。

と、順を追って表現しています。

エクセルに元々入っているコサインと自作のコサインを比較してみると、一致しているのがわかると思います。


ただ、注意事項として、cosの中身のxは°ではなくラジアンという単位を使わないと数値が合わないです。
°というのは一周が360°という単位ですが、どうして1周360°なのかという根拠は曖昧で
約数を多く持つからという意味合いしかありません。
きっと6人とか9人とかでケーキを分けたかったとかそういう理由だと思います。いやまじで。


それに対してrad(ラジアン)は1周を2π(円周率の2倍≒6.28)とします。
これは半径1の円周という立派な根拠があります。




次回の「展開せんかいマクローリン」は！
新キャラ登場！sinとtan。でもなぜにこのブログではcosから始まった！？
次回、「マクローリン展開をExcelのマクロでやってみない試み～パート2～」
おたのしみに


maccrosof介

にほんブログ村