|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回の「展開せんかいマクローリン」は!
コサインのマクローリン展開に成功した管理人であった! あらすじおわり ===== さて、今度はサイン関数のマクローリンもやってみることにしましょう。 sin関数は sin(x)=∑(-1)^n・x^(2n+1)/(2n+1)! なのですが、ここはひとつ邪道に行ってみることにして、 cos(x)=sin(x+π/2) であることを使ってみようと思います。 つまり、x'=x-90°として、cos(x')をsin(x)としてみるのです。 そうすると、マクローリン係数はコサインのときそのままに、サインのマクローリン展開ができてしまうではありませんか。 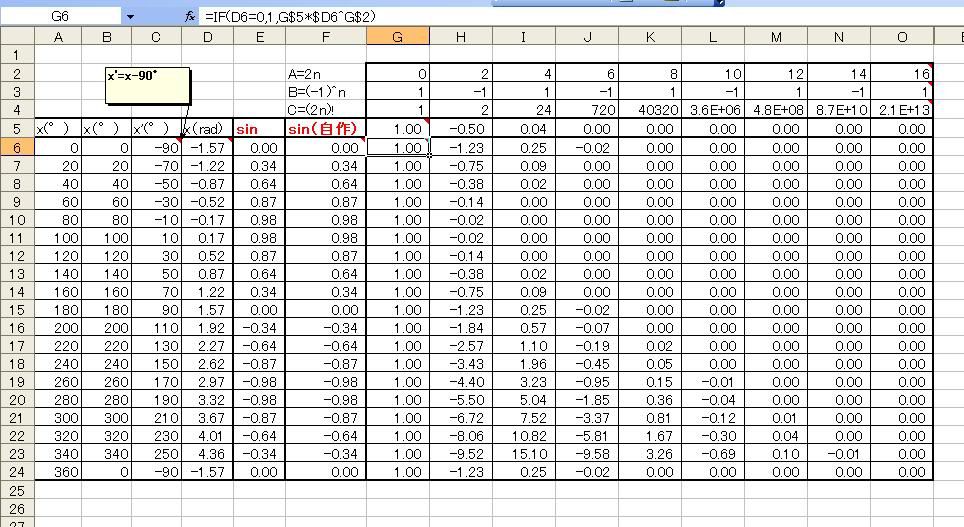 ついでにタンジェントのマクローリン展開もやってしまいましょう。 wikiにはB(ベルヌーイ数)とかいうよくわからない数を使うとかいてありますが心配要りません。 タンジェントはコサイン分のサインじゃないですか。 つまり、cosもsinも作ってしまったわけですから、 tan(x)=sin(x)/cos(x) で計算してしまえばいいのです。 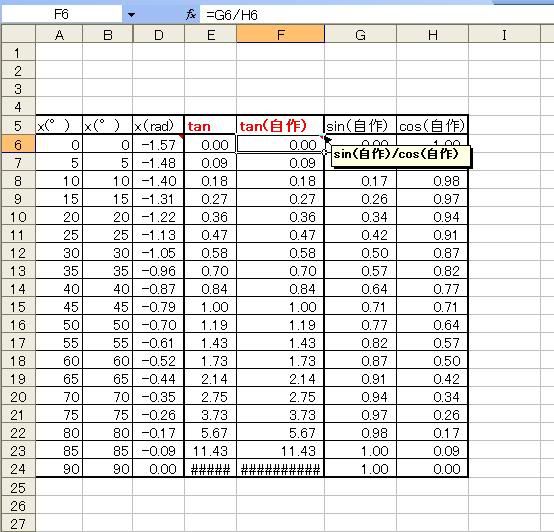 本当はsinもtanも素直に展開するべきなんです。 PCさんはsinとcosを作ってからtanを計算するなんて回りくどいことしたくないでしょうからね。 でもベルヌーイ数とか出てきたら萎えるじゃないですか。 ただ、sinの展開の仕方、これは僕のシュミ一筋です。 つづく?→続いた!  にほんブログ村 PR 

|
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|





