|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
マクロでやらないマクローリン展開シリーズもこれで最終回・・・!にするつもりですいちおう。
マクローリン展開で出せるのは三角関数だけではありません。 ルートなどの無理数も、マクローリン展開で計算されています。 前回まで何度か出てきた円周率πも、マクローリン展開(より一般的にはテイラー展開)で算出されています。 この円周率の計算方法で「マクロでやらないマクローリン展開シリーズ」を締めたいと思います。 sinやcos関数の中身の角度は、1周を360度とする定義よりも、1周を2πラジアンと定義したほうがより根拠があると以前書きました。 では、sinxが1になる、あるいはcosxがゼロになるxは何度でしょうか? 90度ですよね。 ラジアンの尺度を使うとπ/2です。 三角関数を習うときにたいてい出てくる角度は0、30、45、60、90度のどれかでした。 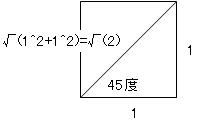 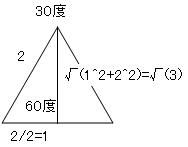 つまり2種類の三角定規の角どれかなわけです。 2種類の三角定規はそれぞれ、正方形と正三角形を半分にしたものでした。 だからこそ、無理数は√(3)や√(2)しか出てこなかったのです。 しかし、どこかテキトーに、sinx=0.642788になるxを答えよ 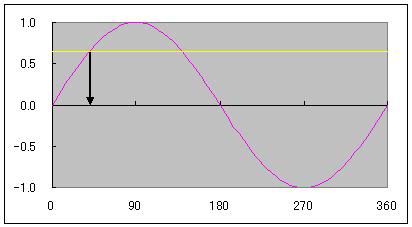 といわれるとどのように方程式を解いたらいいかわからなくなってしまいますよね。 そこで出てくるのが「逆関数」という概念です。 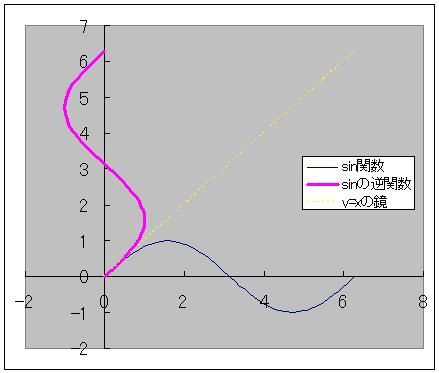 逆関数というのは、図のようにy=f(x)という関数をグラフにイメージしたとき y軸とx軸、縦と横をひっくり返したような関数のことを言います。 ということは、y=xの直線に対して線対称なわけです。 sin関数の逆関数はAsinと書いて、アークサインと呼びます。 cosやtanもAcosやAtanと書いて、アークコサイン、アークタンジェントと呼びます。 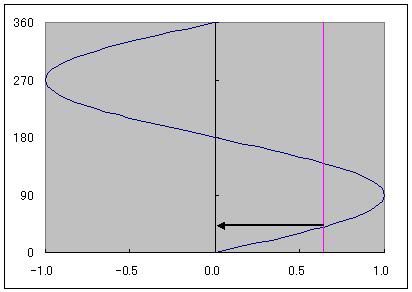 さきほどのsinx=0.642788は、x=Asin0.642788として答えればいいわけです。 このうち、アークタンジェントAtanを使って、円周率πを計算してやるのが今回の目的です。  tan45°は高さ1/底辺1で1ですよね。 ということは逆関数で考えると Atan1=45度となります。 しかし、Atanの値は45度ではなくラジアンでπ/4となります。 このことを利用して、Atan(1)からπ/4を算出してそれをさらに4倍すると、円周率πが計算できるのです。 アークタンジェントのマクローリン展開は意外にも、タンジェント自身のマクローリン展開よりも簡単で ベルヌーイ数なんてものも出てきません。 Atanx=∑(-1)^n・x^(2n+1)/(2n+1) これだけです。階乗すら出てきません。なんだか拍子抜けしますね。 こんなんでどれだけの関数を再現できるのかと不安になるかもしれませんが大丈夫です。 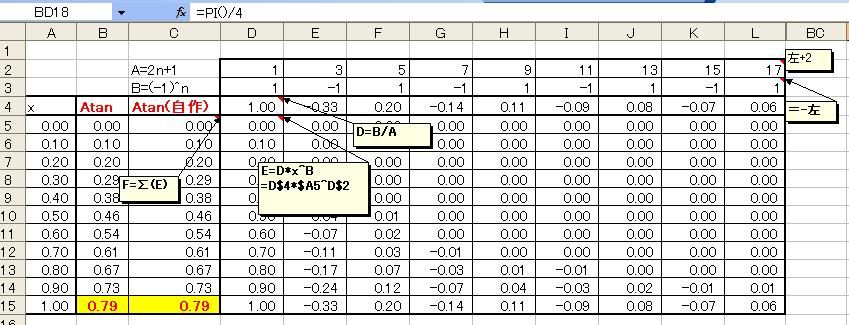 この表のx=1のところを見てください。 atanの値が0.79・・・(0.7854・・・)となっています。 これを4倍すると円周率3.14・・・が出せるのです。 トライアングラー  にほんブログ村 PR 

|
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|





