MWC：歩数計のカロリー消費計算は一体何をやっとるのか！

先日機種変したケータイにようやっと歩数計のハードウェアがきましてね
そのソフトも素敵に充実しているのです。
1日ごとの歩数を記録してくれていて
丸々2ヶ月分くらいは溜め込めるみたいなんすよ


リストやグラフ表示もあり、
歩幅から歩行距離、
歩行距離と体重から消費カロリー
消費カロリーから脂肪燃焼量も同時に表示してくれる優れものなのです！



さて、この歩数計のデータを取り始めてから20日が経過し、データもいい感じに揃ってきたので、解析をしたいと思うのです。



歩数と歩幅があったら、歩数×歩幅から歩行距離は簡単に出せるじゃないですか

消費カロリーから脂肪燃焼量を計算するのも、係数は一定のようでした。

アインシュタインの特殊相対性理論による
化学反応による質量-エネルギー変換効率・脂肪燃焼量・光速の2乗＝消費カロリー

の式から「化学反応による質量-エネルギー変換効率」を換算すると、0.000000000325(3.25A(ストローまないオング))と算出できました。
化学反応だとだいたいそんなもんですよね
_{核融合だとスーパーセント、核分裂は忘れましたが、ブラックホールエンジンの１００％との間に降着円塵エンジンの５０％というのもあるみたいですね}

700kcal消費したら体重が100gくらい減るわけです。



ただ、何キロ歩いたら700kcal消費するのかっていうのがあんまり一筋縄じゃなかったんですよねー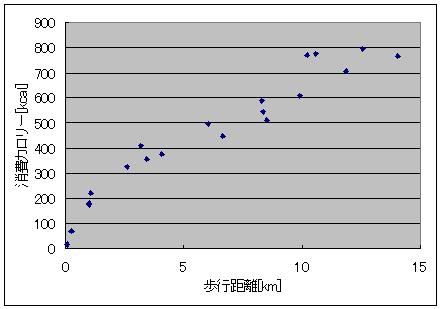


とりあえず、74kgの物体が12kmくらい歩くと700kcalのカロリー消費になって、100gくらい減るらしいんですが、
消費カロリーが単純に歩行距離に比例するってわけでもないようで･･･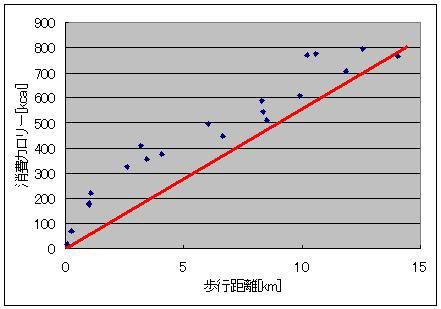


そこで、単純に摩擦に抗ってある体重の物体がある距離を移動した際に使うエネルギー(＝仕事量)を摩擦係数から計算すると仮定して計算してみますと(イメージとしては、さっきの図の赤線を水平にして見たimage.jpgです)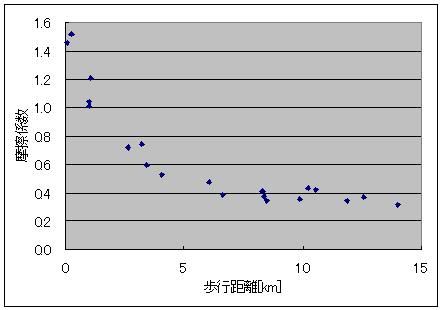


これがまた歩行距離に応じて摩擦係数が微妙に変わるとか言うおかしな計算をこの歩数計はしてやがるみたいでしてね

しかも結構ギザギザなんすよ！


もしかして、一度にまとめて歩いたかどうかも考慮に入れてくれてるんでしょうか
歩いているうちにだんだんカロリー消費が緩慢になってくるみたいな感じの。



摩擦係数でいうと、だんだん体があったまって潤滑が進んでくる感じです
歩き始めは1.5あった摩擦係数(仮)も、6kmを過ぎると0.5近くまで下がってくるわけですよ



それで、少し間を空けてまた歩き出すと潤滑が元に戻ってしまうので
同じ歩行距離でも消費カロリーが微妙に違ってくる、みたいな。



まあ摩擦係数が1以上っていうのも変な話だと思うんですけどそこはまあ

平坦じゃないガタピシを関節ギシギシ滑らせて無理やり摩擦係数として換算した

みたいな状況だとそう算出されてもおかしくないのかなーってかんじ



摩擦係数のだいたいの数字が1を下回っててホッとしたようなそうでもないような。




＝＝＝

で、出てきたこのグラフ
今度はこいつを1つの式で近似してみたいという欲求が沸くわけですよ普通は

そこで登場するのが両対数グラフです。
x軸もy軸も目盛が対数になってるグラフで、0.1の次の目盛は1、その次の目盛は10、さらにその次が100となっている不思議グラフです。


両対数グラフはy=x^nのnがプラスでもマイナスでも小数でも、つまりxの何乗に比例しようが直線で表現してくれる便利なグラフです
普通のグラフでは、y=axの傾きがaをあらわしているのですが
両対数グラフでは傾きがy=x^nのn、つまり何乗に比例するのかをあらわしています。
_{※ただし、y=ax+bのbのような余計なものがついてるとちょっと邪魔です}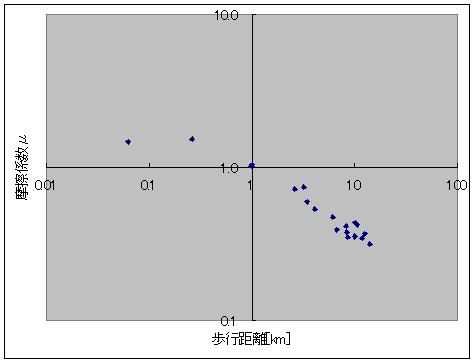


なんかこれどっかで見たグラフですよね
あれすか、アンプ増幅度の周波数特性のボード線図の折れ線近似ですか

まあそんなわけで、このグラフの右側の坂の(両対数での)勾配(傾き：slope関数)を計算することで、どういうわけか歩行距離500m(時定数じゃなくてωRCのRCみたいなあれなんだっけ、折れ線の折れポイントのことなんだけど)以上の領域では摩擦係数が距離のマイナス0.45乗に比例、つまり0.45乗に反比例しているという結果が出ました。
なんで0.45乗なんでしょうね、そんなことはしりません＾＾
そのうちググれれば御の字でしょう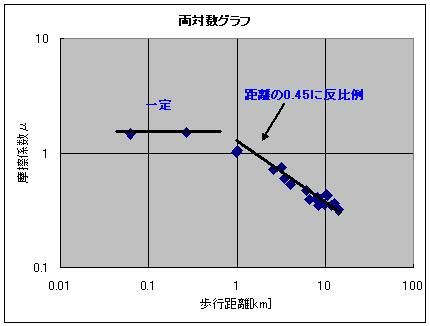


ただ、歩行距離が500m以下の場合はなんだか定数っぽいので
単にx(歩行距離)の-0.45乗ってわけでもないのでしょう
そんなときは(1+x/x0)^(-0.45)としてx0を調整してグラフに合えばいいのです

それでも形だけ合って上や下にシフトしているときは式全体を何倍かしてやればいいです。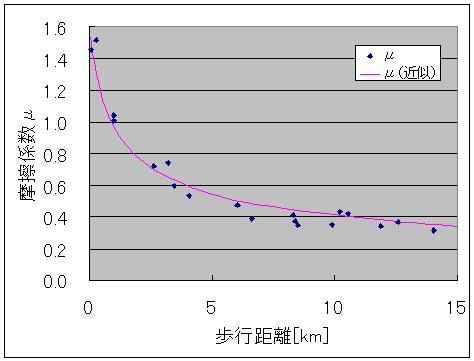


結論
摩擦係数(仮)＝1.6×(1+距離/500m)^(-0.45)
という近似ができました＾＾


つゆうことは、
歩数から軽くなったであろう体重を計算したい場合は

歩行距離＝歩数×歩幅
消費カロリー(そのまま計算するとジュールで出るのでカロリーに直す)＝摩擦係数×体重×歩行距離
摩擦係数＝1.6×(1+歩行距離/500m)^(-0.45)
ダイエットしたカモシレナイ体重＝消費カロリー(calをJに直す)／(3.35ストローまないオング×光速の2乗)

で計算すればいいわけです＾＾


ハイパーーーー　ス　フィルタ

にほんブログ村