PAD：マクローリン展開をマクロでやってみない試み～パート3～

ずーっと前のこと、具体的には2011年の11月20日のことになりますが、
マクローリン展開をエクセル(マクロなし)で説明するっていうのをここの日記でやっていまして
ちょっと中途半端な状態で途切れていたのです。



不調が直ってきたので続きを再開しようかなと。

以前は、サイン・コサインなどの三角関数をマクローリン展開でいちから組み立てる話をしました。
パソコンは基本的に足し算(四則演算)しかできないので、
関数を足し算に還元する仕組みを紹介していたのです。

どこまでも続く数列の足し算、無限級数というのですが
基本的にこれを使えば関数を再現することが可能、という話でした。


しかしながら、パソコンのメモリや速さなどは有限なので
どこまでも足し算していっていたら巨大なパソコンになってしまいますし、いつまで経っても計算が終わりません。
そこで、ある桁数だけ合えばOKって割り切って、それに見合う数だけ数列を足しているのです。


しかし困ったことに、三角関数は関数の上限はあるのに、変数に上限がありません。
sinやcosはマイナス1からプラス1の範囲に収まりますが
関数の中に入る角度の数値は何回転でもできてしまうのです。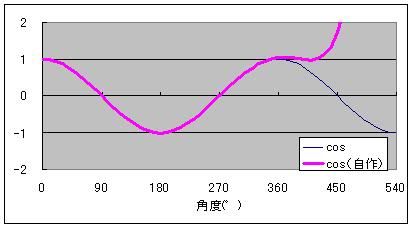


対策を取らずにコサイン720度とかを計算しようとするとおかしな数値が出ます。
なので、せめて360度の周期内に変数を抑える調整が必要なのです。


このとき、変数を周期的にする関数が使われます。
その関数とは、あまり演算です。

分数や小数を習い始めると、「あまり」の存在を意識しなくなりがちだと思います。
16を9で割ったら9分の16とか、1.77777･･･と考えて
1あまり7とかいう発想をしなくなる人がほとんどだと思います。



が、このあまりが大事になってくるのです。


三角関数の場合は、360度周期なので360で割ったあまりです。
たとえば361度は360度で割ったあまりである1度を、改めて変数に置き換えて
sinやcosを出すわけです。


ところが、三角関数の中の変数には1周が360の「度」という単位よりも
1周2πというラジアンを使ったほうがより適切であることから
周期を360度ではなく2πにしなくてはなりません。
つまり2π、無理数で割ったあまりを計算しなければならないわけです。



あまりを計算する関数というのもエクセルには組み込まれています。
mod関数というものなのですが

さきほどの16を9で割ったあまりを出したいときは
mod(16,9)と入力します。

この関数は何をやっているのでしょうか

たとえば、721度を360度で割ったあまりは1度ですよね。
これは、721から、360度を2回かけた720を引いていますね。
つまり、720/360=2という割り算を一旦計算しつつ、頭の片隅によけてあるのです。

721の場合は、721/360=2.0027777･･･の、整数部分だけを切り取って、小数点以下を切り捨てているとも言えます。
切捨てのための関数も用意されていまして、round関数と呼ばれています。


したがって
721/360の整数部分2を取り置きしておいて、
360に2をかけて、721から引くと、mod関数、「721を360で割ったあまり」=1が算出できるのです。


では逆に、マイナス10度はどうなるでしょうか？
-10を360で割ると、-0.027777･･･となります。
この整数部分は、実は0ではなくマイナス1です。
どういうことかというと、あまりは常にゼロ以上でなければならないのです。
といいますか、マイナスのあまりというのを「足りない」と定めて、「足りない」を「あまる」に置き換えると
あまりが必ずプラスになる。
といった感じでしょうか。


マイナス10度→-10あまる→10足りない＝350余る→350度

こういうわけです。

こう考えると、機械でも一律にあまりや周期が計算できるようになるのです。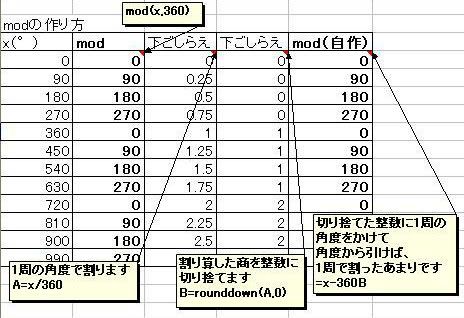


手順としては
関数の中身xを360度周期に抑えるためには
・下ごしらえとしてまずxを360で割り
↓
・割った結果の整数部分nを取り出し
↓
・x-360nを計算する。

これで、すべての角度が0度以上360度未満に収めることができます。



実は、この作業は無理数でも同じことが可能です。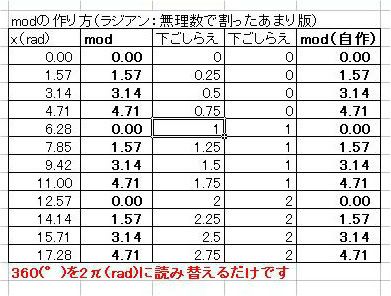



6.29radを2πラジアン周期に収めるためには
6.29を2π≒6.28で割ってその整数部分n=1を取っておき
6.29-2πn=6.29-2π・1≒0.1を変数に当てなおす。
これで無理数の周期化も完了です。
この変数を使って、改めてsinやcos、tanを求めれば、ちゃんとした値が出せるのです。


ぐるぐるモワレぐーるぐるモアレ　次回、最終回

にほんブログ村