MCD：量子力学的円グラフ

グラフの中で円グラフっていうのは僕にとってグラフの中ですごく異端なジャンルに見える。


グラフとして表記する数値が1種類しかなくても成立してしまうし
むしろ1種類しか許容してくれない

それに、上限と下限がある数値にはピッタリの、1周ぐるっと360度。
棒グラフだったら下限はさておいても上限(１００％)を引っ張りあげて改ざんすることが出来るのに対して
円グラフの場合は1周して元に戻るところは選びようがなく決まっている。
これは規格化にピッタリだ。

ただ、2πラジアン360度を１００％とするならば
その半分であるπラジアン180度やπ/2ラジアン90度を１００％とする半円＜ひとつなぎの2象限＞グラフや四半円扇形＜1象限＞グラフがあってもおかしくはないような気がしないでもない
3象限？ないな。



そこで、量子力学的なかんじで、ちょっと奇妙な円グラフを考えてみた。

1乗同士の合計ではなくあくまで2乗同士の合計が１００％になる円グラフ。
その名も、ユニタリーーーーー円グラフ！


しかしながら、
元々円になるようなグラフの横軸数値n個を2乗して合計してルートを取ってからnで割る平均
と
縦軸数値n個を2乗して合計してルートを取ってからnで割る平均
との関係は、残念ながら円にならない！＞＜

平均してからn個で平均取れればいいんだけどねー
円グラフはどうも許してくれないらしい。

わかりやすく式で説明すると
円をあらわすn個のxとy=√(1-x^2)に番号iをふってxi、yiとする。
(√(∑(xi^2+yi^2)))/n　(i：1～n)
と
√((∑(xi^2+yi^2))/n)　(i：1～n)
は違うし
√((∑(xi^2+yi^2))/n^2)　(i：1～n)
としてもムダなのよ！

横軸はあくまでxであってx^2ではないし、縦軸もあくまでyであってy^2ではないからね。
平均した数値グラフをも円にしたければ、(√(∑(xi^2)))/nと(√(∑(yi^2)))/nの関係が円になるようにすることね！
ってこってす。おーまいこってす。




そしたら仕方がないんで、相加平均やめて、相乗平均にしますか。
足し算して割る代わりに掛け算してルートとか取るアレ。

xを実部、yを虚部に置き換えた複素数zの相乗平均だったら、
偏角が相加平均になるから、どうがんばっても円になるでしょ。
っていうか円の方程式上に乗るでしょ。
どうせ半径1だし。楽チンだなぁー



そんなわけでぇー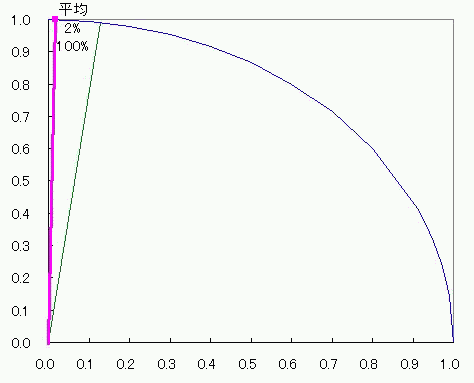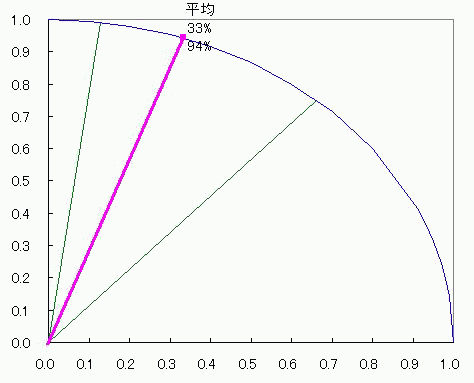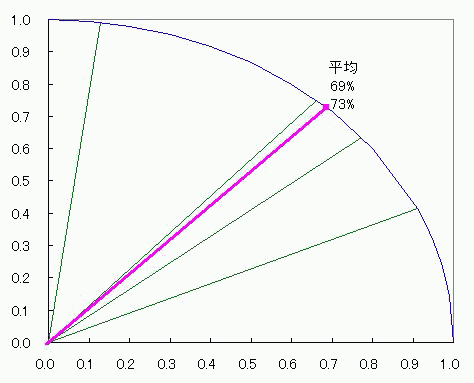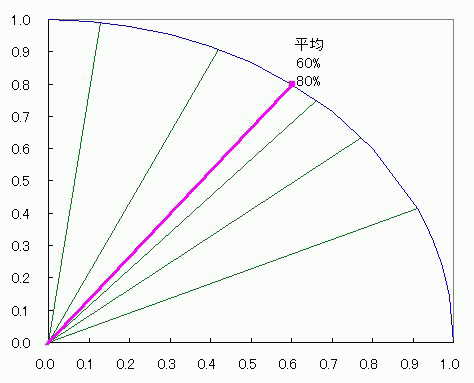

こんなんでましたけどもー！


2つの針の和は最大141V(歌：いとうかなこ)　スカイクラッコの観測者問題

にほんブログ村