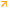|
20080511~
13と7と11の倍数の論理積は13と7と11の積の倍数である。
和ァ・・・
× [PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
いらっしゃいませこんにちは、期待値観測するには確率の問題に超絶疎い、量子きのこです
好奇心はあるのにメンタル不足でソレ系の職業に就けなかったので 何か出来ないかと思ったわけじゃないですが 結果的に物理や数学とかの面白さを伝えられたらいいなー なブログになりました。 このブログをきっかけに、一人でも多くの人が楽しんで物理や数学を学んでくれるとサイワイです。ヽ゚ー゚ノ サイエンスファンタジーなアニメの感想も書きます。 あまり伝わらないようなことを毎日ぼちぼちやっています。 伝わらない・人を選ぶ内容なので、ついカッとなって今は公開しています。 「ブログ村」というブログ紹介サイトにいつもお世話になっております。 ヨカタ!と思ったら押してネ! ※同姓同名の同一人物「量子きのこ」が、pixivにも生息してます。 よかったら覗いてやってください PR
量子力学に関しては、大学生のころに半年間だけ波動力学っぽいのを習ったのと
放送大学で行列力学の具体的な例を習った以外独学だから 体系的な学習ができてなくて順番もぐちゃぐちゃで、あとから「そういうことだったのか~」ってなることがしばしばある。 行列力学についても同様で 放送大学で習った具体例が角運動量(磁気量子数)とスピンのみだったから 「どうしてy軸だけ複素平面の虚軸にいらっしゃるんですか?」 とか 「なんでいつの間にか物理学はベクトル解析という彼女を捨ててクォータニオンと不倫し始めたんですか?」 とか 「結局虚軸ってなに?なんなのよその女!」 っていうのをずっと感じてた。 天下り的に上昇演算子L+と下降演算子L-の定義を って習ったのに関してだけは、放送大学への不信感はあったかな。 それ以外は優秀な教材だった。ありがとう。 なんなんだこのいきなり現れた異世界へのゲートみたいな定義は!? って思ったもん。最近行列力学を学び始めるまで。 大学図書館から本を借りたり、wikiを見たりネット上の演習問題を見たり、AIに聞いたりして 手探りで行列力学への理解を少しずつ高めていったんだけど まずは昇降演算子つながりで、調和振動子の昇降演算子を参考にしてみたんですわ。 波動力学ではすでに知識を得ていたから、行列力学の知識を得たわけ。 そしたらさ、いわゆるハイゼンベルクの不確定性関係みたいな位置と運動量に関する昇降演算子が波動力学同様に出てきて(調和振動子のね) 位置と運動量の行列としての演算子も、昇降演算子から作ることができることがわかったわけよ それで気づいたんだけど 交換関係[x,y]=〇 が定義できるやつはなんかこうなんでも昇降演算子が定義できて まず昇降演算子ありきで位置と運動量の演算子ってのも導出できるのがわかって 交換関係さえ成り立てば、位置と運動量に限らず昇降演算子が定義でき、そっからいろんな物理量の演算子を求めることができて 調和振動子に限らず井戸型ポテンシャルでも似たようなアプローチで定義が可能なのがわかってきて。 それでわかったんだけど 調和振動子の位置xと運動量p から昇降演算子 が求められたのと 角運動量Lのx成分Lxとy成分Ly から昇降演算子 が求められたのって同じプロセスなんだ! って気づいたんだよ。(Lzは角運動量のz成分) じゃあなんで、 と は出番がないんだよ? っていうと、たぶん変数分離と極座標のせい 極座標って直交座標と違って動径rと角度θ(緯度)とφが平等ではなくて 角度(地球儀でいう経度)φに関する微分方程式がめちゃくちゃ楽にできてて Lzの演算子を波動関数に掛け算するだけですぐに固有値が求まっちゃうわけ。 で、なんでLzだけ特別なのかっていうと、たぶんスピンや角運動の主な回転軸だから。 で、ここも俺の勘違いだったんだけど 物理が突然ベクトル解析の彼女を捨ててクォータニオンを愛人にしたんじゃなくて ここで単にアナロジーができたほうが先で こっからパウリあたりが、「この(ヒルベルト空間の)ベクトル、なんか(ベクトル解析の)ベクトルみたいじゃね?」 って気づいて、クォータニオンに(再度)注目が集まって、CGの回転に使われるようになったってのが本来の道順なんだと思う。 だから、虚数単位は相変わらずどうしてそうなのかは人類は知らなくて 突然3次元空間のy軸を担当するようになったわけでもない やっぱり物理は相変わらずwhyではなくhowを問う学問なんだと思う 数式がそうなっているとしか言えない。 未来の人類がまだ「数式がそうなってるからとしか言えない」かどうかはわからないけども
行列力学で定義する物理量演算子の行列さあ、
よく無限次元のヒルベルト空間とかいうけど、 「未知の無数だからまだ具体的には決めてないけど無限ではなくね?」とか思った。 井戸型ポテンシャルとか調和振動子ポテンシャルとか、対称か反対称か結構気にしてるから 偶数か奇数かを気にもするし、無限だったら偶数も奇数もないから、無限ではないんじゃないかなって思うのよ あと、無限次元だったらノルムもだいたい無限になっちゃうし不都合じゃんか 重みでもつけて収束させることになっちまう。 まだ決めてないからn個の固有状態を持つけど nは無数ではあっても無限ではない、なんじゃないかなあ でも波動力学と対極に位置するからあっちこっちで概念があべこべで、まだ全然慣れないなー
大学図書館で本を借りて、AIやwikiも頼りつつ、量子力学の行列力学を勉強してみている。
とりあえず調和振動子について考えてみた。 固有状態が3つだと、位置の演算子はシンプルには以下のように書けるらしい。 ちなみに5状態だと以下のように書け、対角成分から少しずれた非対角成分に√nという形で次々値が入るらしい 3状態の固有値は0と±√3の3つである。 波動力学における波動関数のピークの位置とはなぜか少しズレるのが気になっている。 2状態まではズレないのだけど、3状態からなぜかずれ始める そこで本を読みながら考えていたのだけど 「状態が全部固有状態だからずれるのではないか?」 と思い 固有状態ではない行と列を増やしてみた。 しかしこれの固有値を求めるとやっぱり0と±√3で、波動力学と食い違って見えるのだった。 ただ、それはそれとして、この行列の固有値は0が3つ重複している。 なんかこう「エルミート行列は信頼できる」みたいなのを信じて ウルフラムαで解いてみたところ 固有ベクトルはちゃんと5つ求められることがわかった。 固有値が重解を持つさい、固有ベクトルの求め方は確か3通りくらいあると記憶している。 俺はその辺をいまいちわかってないんだが、なんとなく「エルミート行列を信じる」ことにして正解だった。 物理としては役立ってはいないが、どうもこのエルミート行列というもの、 線形代数の問題としては結構使えるのかもしれない。 随伴行列をユニタリに規格化してやったものUが のようにあらわされ、 逆行列がエルミート共役そのものなので、以下のようになり ちゃんと対角化されて対角成分に各固有値が表れている。 また、これは3行3列の これと物理的な意味は変わらない しかしながら、俺はまだまだ行列力学を習いたてで、なぜ固有値ごとに固有ベクトルがある、というのの「物理的な」意味などがよく理解できていない。 固有状態同士を重ね合わせると何かになるのだろうか?? 固有状態が3つなら3つで変わらないのだから、同じエネルギー準位の話だと思うし 同じエネルギー準位同士での線形結合など波動力学にはない概念のように思うのだけど… あと、行列力学は抽象的なのはいいが、シンプルな例でもせめて本には具体例がほしいと思った。 著者は鍛えているつもりなのか知らないが、具体例の有無で初めて学ぶ人への敷居がずいぶんと変わるように思える。 具体例を載せることで学生が怠けてしまうことを懸念するデメリットよりも、 具体例を載せることで学生の理解を助けるメリットのほうがずっと大きいのではないかと思う
期間があいてしまった。熱が出て寝込んでた。
ところで、2/12の「複2次にした4次方程式」の件だけど これを結論にしたのは失敗だった。 そのうち図解も載せたいのだけど、2θというよりは4θの形にしたかったので ここまでやっておくべきだったと反省している。 ============== それと、2/14の「4=1+3次方程式」のほうで 方程式の係数qとθの関係をまだ算出していなかったので、ここで出してしまおう。 yを算出する途中でuというものをいったん算出するんだけど このuをθで表しておきたいのだった。 そのためにアークタンジェントを3分の1にしたものをθと置くと yは このように簡潔に、かつ整理整頓した形で書くことができる。 ではqとθの関係について分析を始めよう を3倍して となるが、ここでアークタンジェントを2変数から1変数の関数に戻してやると以下のようになる 両辺のtanを取るとアークタンジェントが消える 両辺2乗して ここで、ピタゴラスの定理(三角関数)に気づく tanの2乗に1を足したものはcosの2乗分の1に等しいので 逆数を取ると、分母にきていたqが分子にきて、気持ち悪さも消える 両辺ルートを取ると となって、cosの値は-1以上1以下なので、qの取りうる範囲は-2/3/√3以上2/3/√3以下となり、 前に求めたqの範囲とも一致する。
前回は複二次式(2×2次式)として四次方程式を解いたが、今回は1+3次式として四次方程式を解く。
二次方程式の平方完成・三次方程式の立方完成に続く 四次方程式の同様のそれがすでに済んでいるものと仮定し、二次の項の係数はマイナス1とする。 前回は1次の係数をゼロにしたが、今回はゼロ次の係数をゼロとし、1次の係数をqとすると以下のように書けるが、 yでくくれるので、y=0と、 の3次方程式に分けることができる。 ここで3次方程式に関してはカルダノの公式を用いることにすると uの3乗とvの3乗は以下の定義となる。 ここでpというのは四次方程式におけるyの2乗の係数なのでp=-1である。 つまりこうだ また、この三次方程式の解yが3つとも実数になる条件というのは ルートの中身が負になって-q/2に純虚数が加減されることで uの3乗とvの3乗が複素共役の関係となることなので、以下のように書き換える。 このルートの中身が正の数であれば3つのyすべてが実数となるので、 と整理することができる。 これを因数分解すると このような不等式になるが、2つの積が正であるためには 2つの式両方がプラスか、2つの式両方がマイナスであればよい。 両方がマイナスになるqは存在しないため 両方がプラスになるqを計算すると このような範囲内のqであればyがすべて実数となることがわかった。 さて、yが実数になる条件はわかったが、yは具体的にどのような値になるのか まずはuの3乗とvの3乗の両方の3乗根を取る必要がある。 ここで、u,vの3乗を極形式にするとわかりやすいだろう。 u,vの3乗の絶対値は実部の虚部の2乗和のルートなので定数になって また偏角は となる。 ここでタンジェントの逆関数であるアークタンジェントの引数が2つになっているが これは本来アークタンジェントの1つの引数の範囲が-πからπまでしかないのを -2πから2πまでにするために引数を2つにしたものである。 すなわち、1つ目と2つ目の引数は約分が可能なので、以下のように整理することができる つまり、u,vの3乗は このように極形式に書き直すことができ 3乗根を取るには絶対値はそのまま3乗根、偏角は3で割ればいいだけなので このようにすんなりと表せてしまうのだ。 そしていよいよyの値を求めるのだが 1つ目のyの値はy=u+vである。 vはuの複素共役なので 実部を取り出してこのように簡潔に表現することが可能だ。 そのうえ、オイラーの公式を用いれば実部はコサインにほかならないので さらに簡潔に書けてしまう。 では、2つ目、3つ目の解であるy2、y3はどのようになるか である。 このwとはなんだろう? これは1の3乗根のうち1ではない複素数の2つのうちどちらか1つのことだ。 つまり これのことである。 wを3乗すると1になることを確かめておくといい。 また、w*はwの複素共役のことなので、wの、虚部の符号だけが異なるものだ。 これも3乗すると1になる。 u*=vであることも踏まえてまとめると このように綺麗に表すことができる。 これはつまり であるともいえる。あと、4次方程式としてはy=0が4つ目の解として加わる
二次方程式の平方完成・三次方程式の立方完成に続く
四次方程式の同様のそれがすでに済んでいるものと仮定し、二次の項の係数はマイナス1とする。 ゼロ次の係数をrとすると以下のように書けるが、 これはyの2乗についての二次関数ととらえることができるため、yの2乗について解くと以下のようになり これの平方根を求めるとyが求まるので このようになる。複合は同順ではなく独立である。 yが実数であるためにrはどのような範囲であればよいか? 内側のルートに着目すると1-4r≧0なので rは1/4以下であることがわかる。 また、外側のルートにも着目すると でもある。 変形すると以下のようになるが、 右辺は-1以上1以下なので両辺を2乗しても不等号は変わらず このようになり、2つ目のrの条件なr≧0であることがわかる。 したがって、yの解が実数であるためのrの取りうる範囲は0≦r≦1/4である。 さてここで、 の左辺をグラフ化することを考えてみると 左辺がx軸と交わる点は左右対称であることが想像できる。 yの取りうる値は-1≦y≦1であるので もしかしてこれは三角関数で表せるのではないかと閃いてみると仮定すると y=±sinθ、±cosθだとしたら、θとrの関係はどのようになるだろうか? まずは解であるyを±sinθとおいてみることにしよう ここで倍角・半角の公式を左辺に適用すると となり、cosの2乗の取りうる範囲は0以上1以下なので、rは0≦r≦1/4となり、理にかなっていることもわかる。 y=±cosθもやっておこう こちらも同様であることがわかった。 ±sinと±cosはsinかcosどちらか一方について、90度ずつずれた同じsinかcosであると考えることができるため、yの4つの解は位相が90度ずつずれたsin(またはcos)の多価関数という、シンプルな解釈を得ることができた
前回の続きなんですが、実際にSU(4)の生成子の中の3つの実数と6対の共役複素数から、固有値を求めるための4次の特性方程式を実装し、生成子のエルミート性から4次方程式の解が4つとも実数であることを確かめたのが以下の図です。
対角成分の実数をx,y,zとし、それ以外の共役複素数をa,b,c,d,f,gとして a,b,c,d,f,の実部をa1,b1,c1,d1,f1,g1、虚部をa2,b2,c2,d2,f2,g2とそれぞれ定義し、 15個のパラメータを-0.5~+0.5の範囲で一様乱数として、左から2列目に出現させてみました。 左から3列目は左から2列目の2乗で、一番下に15個の2乗和のルートを算出しています。 15個のランダムの値それぞれをこの2乗和のルートで割ったのを、規格化後として左から4列目に配置しました。特性方程式にはこの4列目のデータを用います。 念のため5列目には4列目の2乗を算出して一番下で和のルートを取り、1になることを確かめています。 そうすると特性多項式のグラフは右のようになり、 x軸と交わる点つまり4次方程式の解は必ず4つあることがわかるかと思います 4次方程式の解はフェラーリの方法で算出しました。
前回の続きですが、SU(4)に使ったa1,a2,b1,b2,c1,c2,d1,d2,f1,f2,g1,g2,x,y,zにrand()-1/2つまり-1/2~1/2までの一様乱数を入れて様子を見てみました。
4次方程式におけるAは純虚数、Bは実数、B+AとB-Aは複素共役、その3乗根同士も複素共役の関係にいつもなるようで、足すと常に正の実数になるようでした。 A>B≧0ってことですね つまりそれに2/3を足したCも常に正の実数で、Cのルートも同様でした。 C≧2/3 √C≧√(2/3) 一度複素数になってから実数の範囲に留まるのは興味深いですね。 SU(4)は変数が多すぎて解析できる気がしないのですが、傾向を見るとほとんど1に近い確率でこうなるようです この傾向まで出せると、ここから先の解析は比較的楽かもしれません
特殊ユニタリ群というのがあってですね、special unitaryの略でSUとよく呼ぶのですが
これは一般にn次の行列のことでして、SU(n)と表記します。 ユニタリ行列は複素行列なのですが、行列式の絶対値を取ると1になるものを言います。 そのうち特殊ユニタリは絶対値を取ることなく行列式そのものが1になるものを言います。 これは数、スカラーでいうところのexp(iθ) (θは実数)に相当していまして ユニタリ行列はよく、長さを変えずに向きだけを変える、拡張された回転を意味するといわれます。 具体的には行列の対角化の際に出てくる固有ベクトルを連ねた、随伴行列がユニタリの形をしているのですが、特殊ユニタリであるとは限らないため、特殊ユニタリを作る生成子というものが存在します。 exp(iθ)のθに相当するもので θが実数なのと同様に、この生成子はエルミート行列です。 実数とエルミート行列、純虚数と歪エルミート行列、長さが1の単位円を描く複素数がユニタリ行列、複素共役がエルミート共役に相当していて エルミート共役は転置して複素共役を取る変換を意味するので 生成子に虚数単位iを掛け算して行列指数関数に入れると、特殊ユニタリ群が生成できます。 また、エルミート行列の固有値は必ず実数になります。 2次の生成子はパウリ行列、3次の生成子はゲルマン行列として知られています。 固有値を求める方程式を特性方程式と呼びます。 生成子はnの2乗から1引いた数だけあり、それら生成子の線形結合もまたエルミート行列になります。 n=2のパウリ行列SU(2)なら4-1=3個、3次のゲルマン行列SU(3)なら9-1=8個あります。 ではn=4のSU(n)ならどうなるでしょうか。 生成子は16-1=15個あり、以下のようになります。 これらを線形結合する場合は、15個の任意の実係数を15個の生成子に掛け算し、足し合わせます。 対角成分は実数で、行と列を入れ替えると複素共役になります。 また、生成子s8は√3で、s15は√6でそれぞれ割ります。 トレースはゼロです。 複素数になる部分は実数と純虚数のペアをまとめて1つの数にして簡略化し 手書きする際に煩わしいので大文字のYは小文字yを√3で、Zはzを√6でそれぞれ割ると定義しました。 また、可読性をよくするため、P,Q,R,Sという変数にまとめました。 この線形結合した行列をλと置き、その固有値をrと置くと、以下のようになります。 4次以上はサラスの公式が使えないため、余因子展開を用いて展開しました。 どうも一般に、SU(n)の特性方程式はn-1の項がゼロになるらしく n-1個の変数をn-1次元と考えた時の距離を規格化して1と定義すると、特性方程式のn-2次の係数がマイナス1になるようです。 SU(4)の場合はこうですね 複素数a~fの絶対値の2乗をA~Fとおくと となります。 そして以下が特性方程式になります。 すべて実係数となり、平方完成、立方完成のノリの4次版のような変換がすでに施されたような式になります。とてもきれいな式で、各変数の出番に対称性があります。 また、この方程式の解はすべて実数となります。エルミート行列の固有値なので。 4次方程式 の解の公式はフェラーリの公式と呼ばれていて、以下のように書けます ここで、赤い複合、青い複合同士は同順ですが、赤と青の複合は独立です。 また、 AとBはそれぞれ で定義されます。 定義の異なるrとAとBとCが出てきますが、4次方程式とSU(4)とでいったん分けて考えてください。すみません。
量子力学の本を返したのでこのチャンスを活かして、調和振動子のほうの昇降演算子の、
空で書けるようになった部分を書きます。 まず、調和振動子ポテンシャルのハミルトニアンを無次元化します。 ハミルトニアンの次元はエネルギーなので、 同じくエネルギーの次元を持つ の2倍でハミルトニアン を割ります。 hにバーがついたのはプランク定数を2πで割ったディラック定数 kはばね定数、mは質量、xは位置、pは運動量、ωは角振動数で の関係があるので、無次元化したハミルトニアンは以下のようになります。 そしてこれをガウス素数っぽく半分に因数分解します。 この片方、どっちか忘れましたがプラスがついたほうをaと置くと マイナスがついたほうはaの複素共役(というかたぶんエルミート共役)a†と書くことができます。 †をどっちのaにつける慣習かは忘れましたが 運動量pにプラスiがついたほうを下降演算子、マイナスiがついたほうを上昇演算子と呼び 波動関数に上昇演算子を左からかけると、量子数1個分だけ固有値がアップした波動関数を 波動関数に下降演算子を左からかけると、量子数1個分だけ固有値がダウンした波動関数を 算出することができます。 ではこの芋づるの端っこはといいますと 一番下の波動関数に下降演算子をかけると恒等的にゼロになることが知られているため、それを利用して微分方程式を解くことで算出できます。 つまり具体的にやってみますと 物理量xとpを微分演算子にして このように解くことができます。(Cは任意の定数です)
前回までは、粘性抵抗と慣性抵抗両方が加わった落下運動の運動方程式の解について
粘性抵抗と慣性抵抗片方ずつに係数を制限して、元々どちらかしか考慮していない運動方程式の解と同じになるかを検証していた。また、それぞれの終端速度についても議論していた。 今回はいよいよ、粘性抵抗と慣性抵抗両方を含んだ状態の終端速度について考えてみる。 微分方程式の解は以下のようになるのだったが このとき、時間t→∞の極限で終端速度vはどうなるだろうか。 cothの中身が大きくなると1に収束するので 分母分子に これは、元の微分方程式である mv'=mg-c1v-c2v^2の加速度(力)v'をv'=0としてvについて解いた2次方程式の解そのものである。 そのうえ、数回前に また、すべての変数、関数、パラメータが正の実数と仮定すると 2次方程式の判別式Dのルートは必ず正の実数であり Dのルート√(c1^2+4mgc2)は必ずc1より大きいため、v=-c1-√(c1^2+4mgc2)/(2c2)の解はありえないこともわかる。
前回はc1≠0、c2=0の条件で解いたが、今度は逆にc1=0、c2≠0の条件で解いてみよう。
となるが、元の運動方程式 も解いてみると 部分分数分解を用いて (A1+A2)v=0 からA1=-A2 初期条件t=0でv=0を与えるとG2=-1となって ここで、式を整理してvの式にする 両辺にv+√(mg/c2)をかけると ここで、右辺の分母分子に これは双曲線関数ハイパボリックタンジェントなので を得、見事に両者は一致する。 また、終端速度については t→∞でv=√(mg/c2)になるが、 これについても元の運動方程式 mv'=mg-c2v^2のv'=0の条件で解くことで、単なる代数方程式として 終端速度v=√(mg/c2)を簡単に得ることができる。 前回、粘性抵抗と慣性抵抗両方を受ける落下運動について運動方程式を解いた。
質量をm、重力加速度をg、速度v、時間t
速度の1乗に比例する空気抵抗の係数をc1、速度の2乗に比例する空気抵抗の係数をc2とすると 運動方程式は以下のように書ける。 速度は高さy方向の下向きをプラスに定義する。 ここで、v^2の係数を1にしたいので、両辺を-c2で割ると ここで、式の簡単化のためG=m/c2、B=c1/c2、A=mg/c2とすると dvの分母に右辺を持ってくると以下のようになる。 両辺を積分してvの式にすると、速度vについての運動が解けるのだが、vの2乗が邪魔でうまく積分できないので、部分分数分解を用いる。 という恒等式を作り、A1、A2、Dがいくつになるのか定めることにする。 まず、 なので、 次にA1とA2を定める。 v(A1+A2)=0 からA1=-A2が導かれるので B/2(A1+A2)もゼロである。 D(A1-A2)=1にA1=-A2を大入して、 そうすると元の微分方程式は なので積分ができ となる。G2は任意の積分定数。 対数同士の引き算は対数の中の割り算として引っ込めることができるため 両辺に2Dを掛け算して (ここでG2はまだ任意の定数なので、2DG2を新たなG2として上書きする) 両辺の指数をとって (ここでもexp(G2)を新たなG2として上書きしている) 左辺の分母分子に2を掛け算してやると 初期条件 t=0でv=0を与えて任意の定数G2を定める。 微分方程式の解は となる。 これをvの式に直す。 両辺に(B+2D)と(2v+B+2D)を掛け算する。 展開すると 全部左辺に移行し、vを含むか含まないかで整理すると ここで1/(2v)の式に着目してみることにする。 第1項は約分できるので 問題は第2項だが ここでようやく2vの式に戻すと
次のページ>>
|
カレンダー
カテゴリー
最新CM
[08/08 さつ香]
[12/30 buy steroids credit card]
[09/26 Rositawok]
[03/24 hydraTep]
[03/18 Thomaniveigo]
最新記事
(01/01)
(03/19)
(03/18)
(03/18)
(02/23)
(02/14)
(02/12)
(01/03)
(09/23)
(09/23)
(02/11)
(05/30)
(05/28)
(05/28)
(05/27)
最新TB
プロフィール
HN:
量子きのこ
年齢:
44
HP:
性別:
男性
誕生日:
1981/04/04
職業:
WinDOS.N臣T
趣味:
妄想・計算・測定・アニメ
自己紹介:
日記タイトルの頭についてるアルファベットは日記の番号です
26進数を右から読みます 例:H→7番目、XP→15(P)×26+23(X)=413番目。 A=0とする仕様につき一番右の桁はAにできませんのでご了承くださいズコー
ブログ内検索
アーカイブ
最古記事
(05/11)
(05/11)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/13)
(05/14)
(05/14)
(05/14)
(05/14)
(05/16)
(05/16)
(05/16)
アクセス解析
|