マクロなしエクセルで実対称行列の固有値問題と高次方程式を解く！

n^2行列に見立てたセルに具体的な実数を入れておき
適当に見繕った固有値倍の単位ベクトルを引く
さらに、その行列式を計算し、


具体的な固有値を循環参照で変動させる。


算出した行列式がゼロを横切ればそこは固有値でしたってオチ。


何行何列の何次方程式になろうが(何は同一のものとする)
実数で対称な行列であれば固有値はすべて実数になるため
固有値を揺らす範囲は実数内でおｋという安全・安心・お手軽さ！
数値計算なので5次以上の解の公式云々は関係ない･･･！なんてこった！＞＜

循環参照は幅や高さ、奥行き(シート)に左右されないから、
2次元配列とも見なせる行列が相手だろうと劣化しない！

その上、時を司りる(×つかさどる○つかさドリル)女神であらせられる循環参照ベル・ダンディさんは
別に揮発性でもなんでもないんだからねっ
揮発か不揮発かすらコントロぉール可能なのだぁーフゥーッハッハッハ


ここまでマクロ一切なし。
マクロなしだって、固有値が解けるんだ！^{ﾊﾟ～ﾊﾟﾊﾟｯﾊﾟ～}
まあ、答え合わせにmatrixアドイン入れてたのは内緒。
で･･･デターミナントとトレースだけで答え合わせしたんだからねっ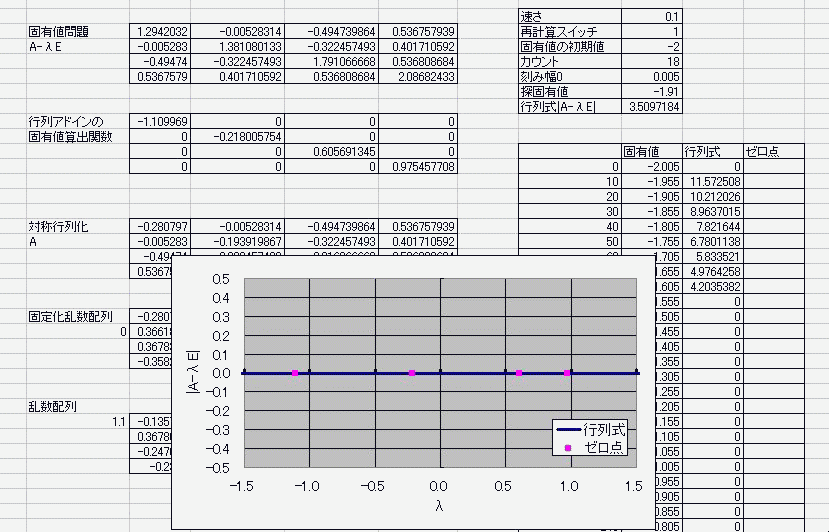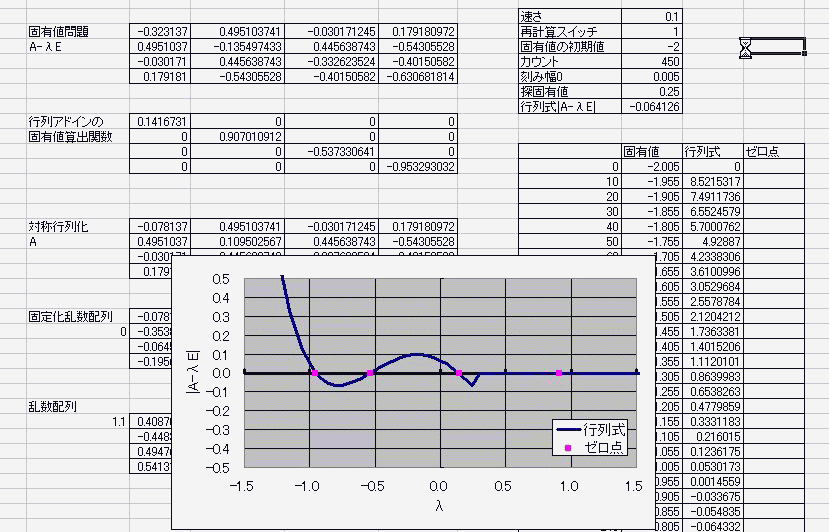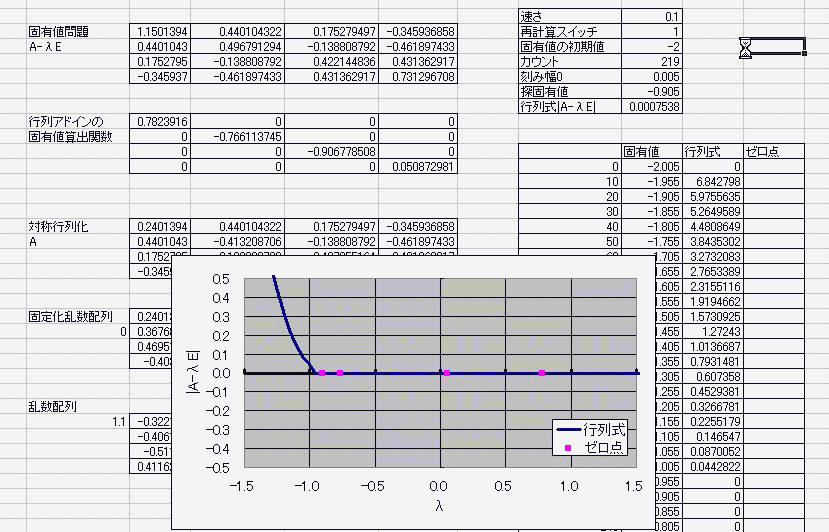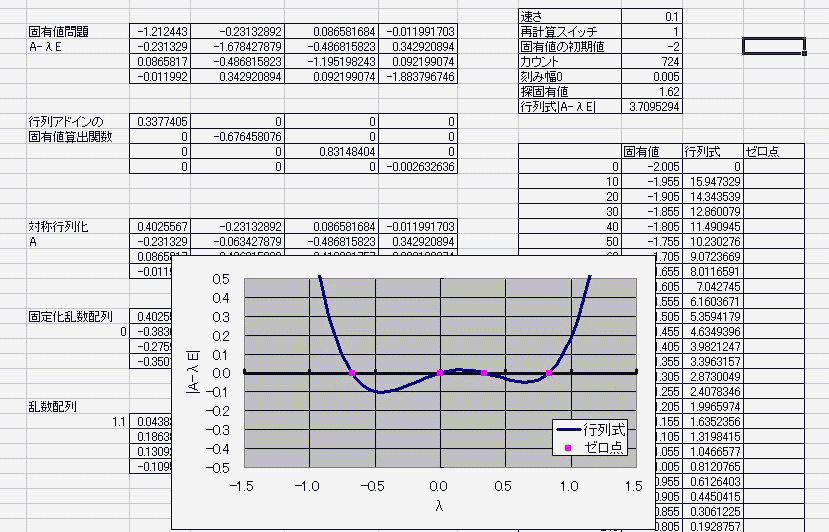



ただ･･･現状では(二分法使っておきながらも)精度がよくないのと
全自動とはいえないのと
重解のときの対処が人力であることなどが課題で･･･


そ、それと･･･エルミート行列の固有値が実数になる証明をまだ理解していなかったりしてー･･･

にほんブログ村