3次に因数分解できる4次方程式の実数解

とりあえずちょっと訂正

x^4-x^2+px=0
の解は


であることが、フェラーリの方法からわかった。

カルダノの方法と比べると
λ(λ^3-λ+q)=0
 
なるほどそっくり。

xの絶対値がとれればなあ
あとなんで偏角を3じゃなく2で割ってるのかよくわからない
まあ4次方程式(4分角の定理)だから必要っちゃ必要な手順なんだろうけど、これと符号の件は関連するのかしないのか

理想としては
3じゃなく2で割りながら、符号も含めて一致させたい

もしかして、6分角の公式とかが必要だったりするんじゃねえだろうな
でも6次方程式が出てきたら手に負えんぞ。せめて複3次とかで勘弁してほしい

3次としても解ける4次方程式の実数解

昨日の続き。
とりあえず符号は置いといて計算を続けます。



3倍角の公式より


なので


また、二重根号の中身の分子は以下のように因数分解できるため、二重根号は二重根号たりえないことがわかった！

 


倍角(半角)の公式も使って簡素化していく。


として、加法定理を用いて係数を比較すると



よって、


(符号はあとで考える)
というのが、x^4-x^2+px=0の解だと思いますたぶん

3次に因数分解できる4次方程式の実数解

まあ、単にλ^4-λ^2+pλ=λ(λ^3-λ+p)=0ってだけです。
違うのは、λ=0も解に含まれることですね。


カルダノの方法を純粋に使ったやつと
カルダノの方法を含んだフェラーリの方法とでやって検算してました。



いちおうここまでは合ってるっぽいです。

ここでいうA41というのはλ^3-λ+p=0のpのことです。

θとA41は、次のような関係があるのですが
つまりA41の範囲は|A41|≦2/3/√3になります

これをそのままA41に代入すると、時折符号が反転する(いつもではない)不具合が出るうえに


(赤い±だけ複号同順でない)
ここまで整理したところで、二重根号をどうやってほどけばいいのか難儀してます。

4分角の定理「俺の屍を超えていけ」

複二次な四次方程式の実数解を解析的に解いて、幾何学的な意味を求めるところで力尽きました

規格化された特殊ユニタリ生成子を全部線形結合させたエルミート行列の固有値
を求める方程式は

n-1次の係数がゼロ、n-2次の係数がマイナス1になるため

たとえば4次だったら

λ^4-λ^2+pλ+q=0
といった風になります。

そのうち、p=0に限定したのがこの図となります。
実数解であるために、エルミート行列は0≦q≦1/4を要求する。
(4分角の定理が大変参考になりました)


見ての通り、四次とはいっても、パウリ行列系に毛が生えた程度の二次っぽさなので
対称性がまだすごく高いです。


 
pもqも一般化する前に

q=0で3分角の定理を適用した3次方程式に立ち寄ってみましょう
こちらではちゃんと固有値の対称性が破れてくるんですよね。



カルダノは空で言えるのに
フェラーリはまだなのよね～

どうしても煩雑になってしまう。
(手書きでやってるからかもしれないけど)

p、qともに一般化したら、円がどんな風になるんだろう
1つ増えた自由度で、半径が変わるのか、偏角が変わるのか
それとも平行移動したりするのか

やっぱり解析解を見るのが一番手っ取り早いんだろうなぁ

しかしそれ以前に、二重根号をほどけるかどうかが心配ﾃﾞｰｽ

4分角の定理(自明)が半分うまくいって半分うまくいかない

8cos^4(θ/4)-8cos^2(θ/4)+1-cosθ=0

を、cos^2(θ/4)=Xとした2次式を解くのは問題なくできる。

cos(θ/4)=±cos(θ/4)、±sin(θ/4)は出せたし

たぶんsin(θ/4)=±cos(θ/4)、±sin(θ/4)だって出せると思う。

でもこれを4次方程式としてフェラーリとカルダノで解くのは結構煩雑

どっかでミスる気がする。というかミスってるのかどうかすらよくわからない。
どの程度細かくしてバグを取ればいいのか。細かくしたら切りがないぞ


もし、4次式が2次式を参考とかゴールフラグにできれば少し荷が軽くなっているのかもしれない。


でも、僕が解きたいのは4分角の定理そのものじゃなくて

4分角の定理を踏み台にした、4次の特殊ユニタリ生成子のエルミート行列の固有値の解析解なんだ。

当然、1次の項が出てきて邪魔なので、複2次として解くことはできなくなる。

1次の項が出てきてもなお、何かしら幾何学的な法則がないか、知りたいんだ。


4次方程式は、内部に3次方程式と2次方程式をマトリョーシカのように搭載してるからなぁ
解析解を求めるとなると記号の付け方がどうしても煩雑になるんだよ。




ちなみに、エルミート行列の固有値を求める方程式を、解析的に整理するのはほぼほぼ諦めましたorz
ミスが多すぎて太刀打ちできない・・・

とりあえず実数解を4つ持つ係数の4次方程式を仮定して、ってやるつもりです


5次？そんな高望みはしません。＾＾＃
そういえば、5次方程式のwikiがあるんですね。何書いてるのかさっぱりわかりませんが！

みんなの愛したタコ式

あ、多項定理って普通にあるのか・・・。気づかんかった。今度使おう。

3分角と3次方程式、その後

あのあともう少し考えてみてたんですが、

実数解もちゃんと3つ、cosつまり-1から1までの間にありましてね

cos(x/3)=cos{(x+2πn)/3}
sin(x/3)=sin{(x+2πn)/3}

だったことがわかりました


　　　　　　　∧∧
　　　　 　　ヽ(･ω･)/　 　ｼﾞﾒｰ
　　　　 　＼(.＼ ノ
　　　　､ﾊ,,､　￣
　　　　￣


しかしよく見るとこの式、やっぱりまだちょっとおかしいですね。
 
qにつく符号が一部、逆になったままです。

3分角の公式(自明)

3倍角の公式を、オイラー・ドモルガンの関係から導きます。




二項定理で展開し、実部と虚部を比較すると、3倍角の公式が出来上がります。


じゃあ3分角の公式は？

3x=Xとすると、3倍角の公式は3分角の公式になりますよね

cosxについての3次方程式を解いてみましょうか。

cosx=c、cos3xをc3とでもおきましょうか。

カルダノの方法を用いて、cが実数になる範囲で解いてみましょう。

 

途中で変数を定義しますと、このようになります。累乗根を求めやすいように、極座標にしちゃいましょう。

 

3乗根を取ると、このようになります。
複素3乗根なので多価なんですが、ここでは1つだけ代表します。

 
v1とv2の組み合わせとして、3v1v2=pになるような条件があるのですが、ちゃんと成り立っていますね。

求めたいcは、v1とv2の和です。複素数なら一般に3つあるのですが、実数の範囲内ではこれだけです。

 
それでは、pとqを代入してみましょう。


こうして世にも自明な恒等式が導かれたのであった・・・orz

二次元での任意軸回転

以前、ちょうつがいの式と題して、

MMDの多段ボーンの理論のようなことを書いたことがあったのです。


これとかこれとか

  
一旦重心を原点に移動して、原点周りの回転をさせてから、元の位置に戻す。



それよりもっと前に、二次元での任意軸回転で困っていたことがあって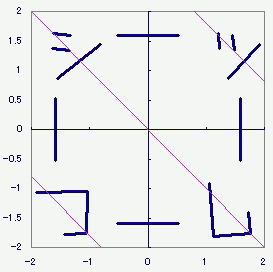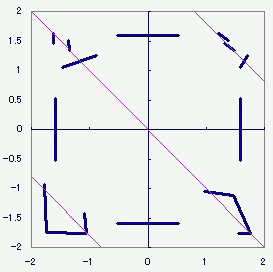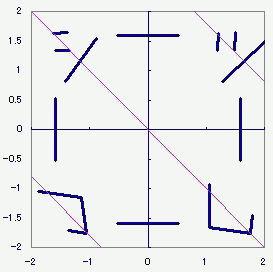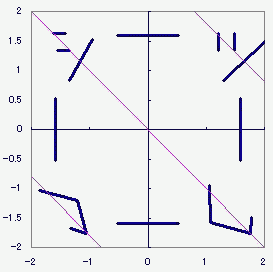


反逆関数
ようやく気づいたんですが、傾いた直線を軸に回転させたければ
１．その傾いた直線ごと、図形をまるっと一旦x軸かy軸まで持っていって
２．それから回転なり反転なりさせて、
３．それから図形ごと傾きも元に戻せば

よかったんじゃないすか


気が付かなかったなぁ

3次方程式と3分角の定理

解が実数になる範囲で解いたら
cos(θ/3)=cos(θ/3)

って自明な恒等式がただ得られただけだった・・・還元不能ってこういうことを言うんですかね？

行列から別の行列を生成！２

n次エルミート行列の固有値を求めたい際にn次多項式を生成したとして、
その係数を数値的に算出するのもまた、最小自乗法の行列だったりする


その行列の固有値を求める際に作った多項式の係数を算出する行列の固有値をry
切りがないのだろうか



いやちょっと待てよ、
１回ずつ入れ子になるにつれてnが減るんじゃないか？めでたしめでたしか？



あれ？もしかして最初の一撃で複素が実数になって壊滅的に自由度減った？


それにしても、情報が姿を変えて残ったり減ったりするのは、
ブラックホールの量子情報問題を彷彿とさせますね



こうやってn次エルミート(対称)行列を作ってやれば数値的にはどんな高次方程式でも解けるばかりか解が実数になるし
ペロンフロベニウスの定理を用いれば、非負行列の固有値が複素数になるにもかかわらず、その絶対値が一番大きいのも実数に保証されるのに、
たかが16や17次方程式の解の公式が解析的な数式データですら読みきれないほど膨大なものになるっていうのは悲しいというか意外というか

ベクトルのプリントをなんとなーく見ていてなんとなーく違和感

内積と外積は分けるべきだろうかとふと思った


一旦混ぜて多項式のように演算しておいてからの
スイッチングで内か外か選べるようにしたほうがいいんじゃね？とか思った。

まあ結局は同じことなんだけども。


でもなんだろう、内積と外積の結果両方ほしいって需要はあるのかな？
現代の表現ではXOR(・、×)だけど
AND(・、×)って需要はないんだろうかと思ったりして。
まあ、そんときゃ内積と外積を足せばいいだけか・・・
というか、両方ってANDでよかったっけ？むしろ全部ほしい状況なんだからOR(・、×)じゃね？
結果は掛け算じゃなくて足し算されるわけだし(線形的に考えて)


VectorKakezan(A,B,内)
VectorKakezan(A,B,外)
VectorKakezan(A,B,内外)
VectorKakezan(dimension,A,B,io)

位置らないベクトルの「名前」もほしいな

天井関数と床関数の差

が1なのは当たり前すぎて誰も言わないのか？？wikiにもない



それにしても、床関数と天井関数
rounddownとroundupを正負で場合分けして処理したらだめっぽいな
if(x>=0,roundup(x,0),rounddown(x,0))
みたいな感じで。
xが整数のときにバグるっぽい


床関数をint関数で表現してやって、天井関数を逆算したほうがよほど健全っぽい

取り急ぎだからよくわかんなくなったけど
wikiのフーリエ展開見たっけ「差が１」の定理は合ってるみたいだから、どっちが正解なんだろう

あ、そういえば

オイラーの公式の、ありそうであまり見かけない変形

exp(ix)/cos(x)=1+i*tan(x)

で思い出したんですが

クォータニオンが中身のsinとcosをオイラーの公式ばりに組み合わせれば
過去の日記のクォータニオン指数関数に一致するかどうかで検算ができるじゃん！

まあ、sin^2+cos^2=1で検算しておいてもいいよね。あ、でも2乗の計算が面倒かもですね

昨日の日記が色々おかしい

かといって訂正バージョンを書こうにも、意外と分量がひどすぎた

まだ計算途中。

法事もあって疲れたのでそろそろ寝る

いつ計算終わるかな・・・


っていうかなんかこうもっと有意義な日記を書きたか・・・た・・・。ｶﾞｸｯ


今日は僕の法事
なんてこたない
何年後になるかな



デジタル－デシマル・コンパレバータ